浮点数的规格化
- 默认情况下,同一浮点数可能有多种表示形式。即可能有多种阶码和尾数的组合表示同一数字。
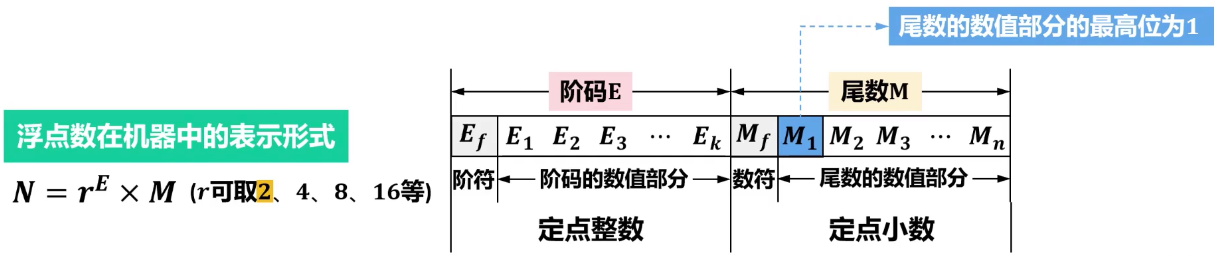
- 通常要求浮点数在数据表示时对尾数进行规格化处理,即使得尾数的最高数值位必须是一个有效值。
- 好处
- 使浮点数形式唯一
- 使浮点数精度最高
规格化方法
- 规格化:将浮点数的尾数调整到特定范围,使每个数值都只有唯一的浮点表示形式。
- 左规:当浮点数运算结果的尾数不满足规格化要求时,将尾数向左移动,同时阶码相应减小。
- 条件:
- 对于原码/反码表示:尾数小数点后的第一位为 0时(如 0.0xxxx…),需要左规。
- 对于补码表示:需要判断对应原码是否已规格化。
- 如对于 ,先转扫描法为原码 ,发现未规格化
- 规格化后原码为 ,即补码为
- 单符号位应满足
- 原码:
0.1xxx或1.1xxx - 补码:
0.1xxx或1.0xxx(即前两位互异原则)
- 原码:
- 双符号位应满足
- 原码:
00.1xxx或11.1xxx - 补码:
00.1xxx或11.0xxx(即第二三位互异原则)
- 原码:
- 操作:
- 尾数左移一位,阶码减 1。
- 重复此过程,直到尾数满足规格化要求(例如,原码尾数小数点后第一位为 1,或补码尾数符号位与数值位不同)。
- 条件:
- 右规:当浮点数运算结果的尾数发生溢出(即尾数绝对值大于等于 1,小数点左边有非零位)时,将尾数向右移动,同时阶码相应增大。
- 条件:通常发生在浮点数加减运算后,尾数和的绝对值大于等于 1。例如,补码双符号位表示中,尾数出现 01.xxxx… 或 10.xxxx… 的形式。
- 操作:
- 尾数右移一位,阶码加 1。
- 重复此过程,直到尾数满足规格化要求(即尾数绝对值小于 1,小数点左边只有符号位)。
- 影响:最右边的有效数字可能会丢失,导致精度损失,但这是为了将数值调整到可表示的范围内。
- 基数 r 对数的表示范围和精度的影响
- 在阶码位数固定的情况下,基数 r 越大,浮点数的表示范围越大。
- 阶码每增加(或减少)1,实际数值的变化是 r 倍。基数越大,阶码相同的变化量能表示的数值范围跨度越大。
- 在尾数位数固定的情况下,基数 r 越大,浮点数的相对精度越低。
- 相对精度:基数越大,尾数每移动一位,其代表的数值变化量就越大(例如,基数 2 时尾数一位代表 1/2,基数 16 时尾数一位代表 1/16)。这意味着在相同的尾数位数下,相邻两个可表示的浮点数之间的间隔会更大,数值的密集程度下降,从而导致相对精度降低。
- 尾数利用率:基数越大,尾数中可能出现更多的前导零(例如,基数 16 时,一个十六进制位相当于四个二进制位,如果这个十六进制位是 1,则二进制表示为 0001,前导零较多),导致尾数位的有效利用率降低。
- 在阶码位数固定的情况下,基数 r 越大,浮点数的表示范围越大。


浮点数规格化后的表示范围
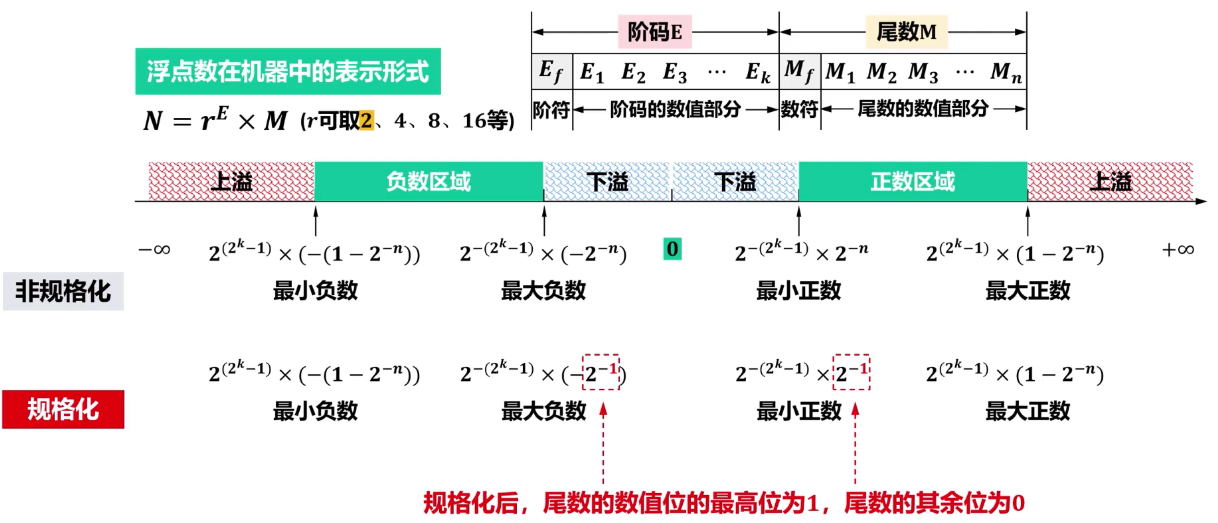
| 类别 | 表达式(非规格化) | 表达式(规格化) | 说明 |
|---|---|---|---|
| 最小负数 | 数值最小的负数 | ||
| 最大负数 | 数值最大(最接近 0 )负数 | ||
| 最小正数 | 数值最小的正数 | ||
| 最大正数 | 数值最大的正数 | ||
| 上溢 | 超出最大正数或小于最小负数的范围 | 超出最大正数或小于最小负数的范围 | 无法正常表示的过大数值 |
| 下溢 | 绝对值小于最小正数或大于最大负数的绝对值 | 绝对值小于最小正数或大于最大负数的绝对值 | 通常当作 0 处理 |
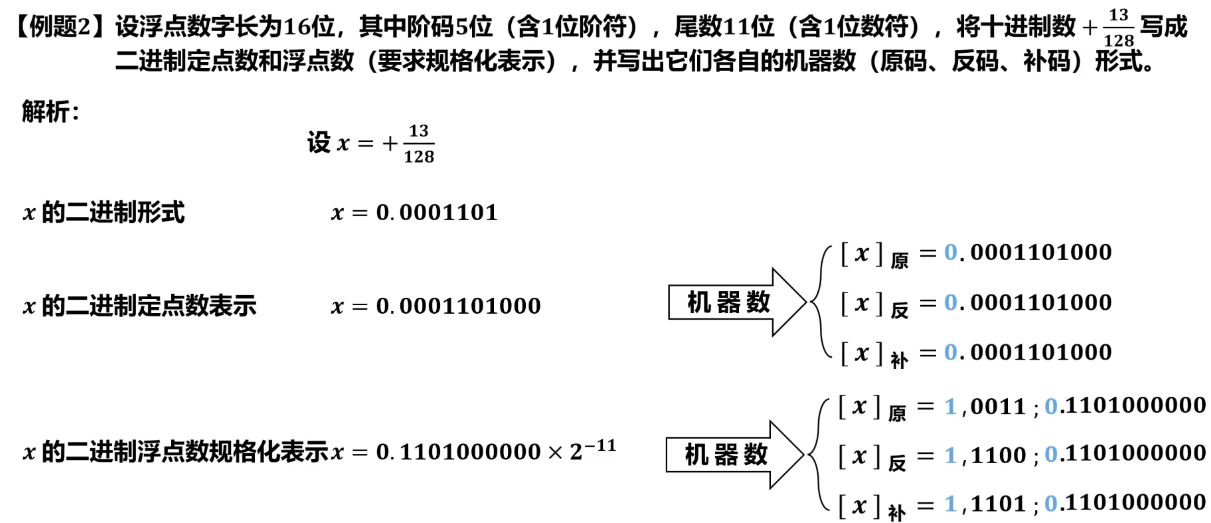
例题

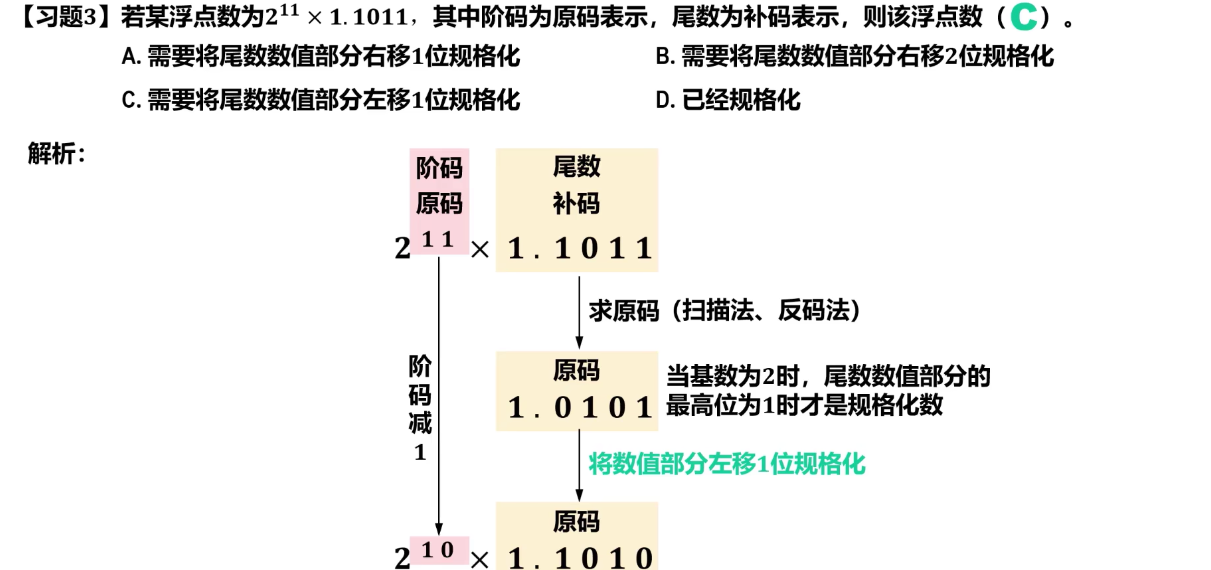
注意不同基数对规格化的要求不同
