226 浮点运算

浮点运算

206 浮点数的规格化

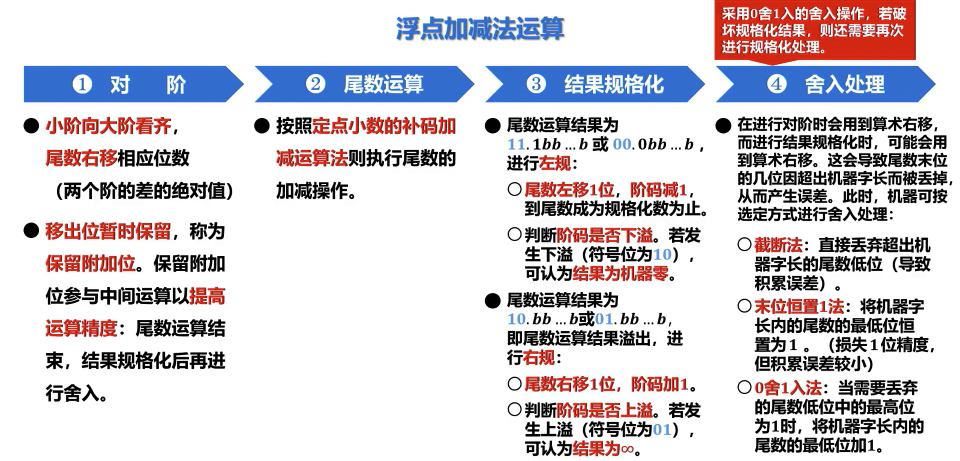
浮点加减法运算

• 对阶：通过移动尾数和修改阶码，使两个浮点数的阶码相等。通常小阶向大阶看齐，小阶的尾数右移。此步骤的目的是使小数点对齐，避免因阶码不同而导致运算错误。否则会丢失尾数高位，造成严重数值错误。
• 尾数加减：将对阶后的两个浮点数的尾数按带符号数（通常为补码）进行加或减运算。符号位参与运算。
• 规格化：调整运算结果的尾数和阶码，使其满足浮点数表示的规格化形式（通常为尾数最高有效位为 1）。
  • 左规 (Left Normalization)：
    • 条件：运算结果的尾数最高位（小数点后第一位）为 0，即未达到规格化要求（如 0.0xxxx）。
    • 操作：尾数左移一位，阶码减 1。重复此过程直到尾数最高位为 1。
    • 判断阶码是否下溢：在左规过程中，若阶码减小到小于机器所能表示的最小阶码，则发生阶码下溢（Underflow），表示结果过小，可置为 0。
  • 右规 (Right Normalization)：
    • 条件：运算结果的尾数出现溢出（如尾数最高位与符号位相同，对于补码表示为符号位与最高数值位不同，或尾数绝对值大于等于 1，如 1.xxxx）。
    • 操作：尾数右移一位，阶码加 1。
    • 判断阶码是否上溢：在右规过程中，若阶码增大到大于机器所能表示的最大阶码，则发生阶码上溢（Overflow），表示结果过大。
  • 双符号位溢出表示法：
    • 00：表示正数。
    • 11：表示负数。
    • 01：表示正溢出（结果为正，但数值超出表示范围）。
    • 10：表示负溢出（结果为负，但数值超出表示范围）。
• 舍入：对规格化后的尾数进行舍入处理，以保证运算结果的精度。当尾数右移或对阶时产生多余位时，需要进行舍入。常见的舍入方法有：
  • 截断法（Truncation）：直接舍弃多余的位。
  • 0 舍 1 入法：类似于四舍五入，根据被舍弃的最高位决定是否进位。若舍入后破坏了规格化结果，则还需要再次进行规格化处理。
  • 恒置 1 法：将被舍弃位的最高位设置为 1，其他位舍弃，然后进行加 1 操作。
  • 最近偶数舍入法（Round half to even）：IEEE 754 标准采用的舍入方法，避免了累积误差。

IEEE 754 浮点加减法运算

IEEE 754 浮点数的加减运算与（上节课介绍的）基于补码表示的浮点数的加减运算有如下不同：

1. 阶码运算规则：

   • 在对阶和结果规格化过程中，涉及到阶码的加减运算时，采用移码的加减运算规则。

2. 尾数运算规则：

   • 尾数运算采用原码运算规则（即符号位单独处理，数值位直接进行加减）。
   • 隐藏位（即规格化浮点数尾数整数部分的隐含 1）要参与尾数运算。在运算前，隐含的 1 需要显式地补上，成为 1.xxxx 形式。

3. 隐藏位参与尾数规格化判断和规格化过程：

   • 规格化判断与调整：
     • 若尾数形式为 1.⋯⋯（即整数部分为 1），则为规格化尾数，符合 IEEE 754 规格化表示。
     • 若尾数形式为 0.⋯⋯（即整数部分为 0），则需要进行左规（将尾数左移 1 位，相应地将阶码减 1），直到尾数规格化（即变为 1.⋯⋯）为止。
     • 若尾数最高位发生进位，形成 10.⋯⋯（即整数部分为 10），则需要进行 1 次右规（将尾数右移 1 位，相应地将阶码加 1），使其变为 1.⋯⋯ 形式。

4. 舍入处理：

   • 就近舍入（Round to Nearest, Ties to Even）：舍入为可表示的最近的数。如果数据正好处于两个可表示的数的中间，则向偶数（即最低有效位为 0）舍入。这是 IEEE 754 标准的默认舍入模式，可将平均误差降到最小。
   • 朝正∞方向舍入（Round towards +∞）：总是取右侧（即数值更大）可表示的最近的数。
   • 朝负∞方向舍入（Round towards -∞）：总是取左侧（即数值更小）可表示的最近的数。
   • 截断处理（Truncation / Round towards 0）：直接丢弃多余位，相当于朝 0 方向舍入。

5. 溢出判断：

   • 浮点运算的溢出（上溢或下溢）主要通过阶码的范围来判断。205 浮点数的表示形式和表示范围
   • 对于 IEEE 754 单精度浮点数（阶码为 8 位，偏置值为 127）而言：
     • 上溢（Overflow）：当运算结果的阶码大于最大可表示的规格化阶码（即偏置阶码 254，真值 +127）时发生。此时结果通常表示为正负无穷大 (±Infinity)。例如，向右规格化导致阶码超过 254。
     • 下溢（Underflow）：当运算结果的阶码小于最小可表示的规格化阶码（即偏置阶码 1，真值 -126）时发生。此时结果可能被表示为非规格化数（阶码为 0，真值 -127）或直接舍入为零。例如，向左规格化导致阶码低于 1。
     • 特殊阶码值：
       • 阶码全 1 (11111111，偏置值为 255) 用于表示无穷大 (±Infinity) 或非数 (NaN)。
       • 阶码全 0 (00000000，偏置值为 0) 用于表示零 (±0) 或非规格化数 (Denormalized Numbers)。

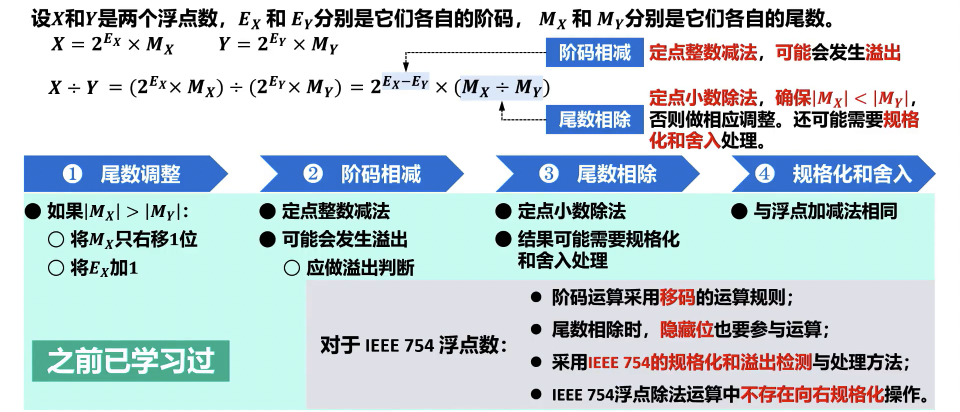
浮点乘法运算（仅了解）

• 阶码相加，尾数相乘。
• 结果的规格化与舍入。

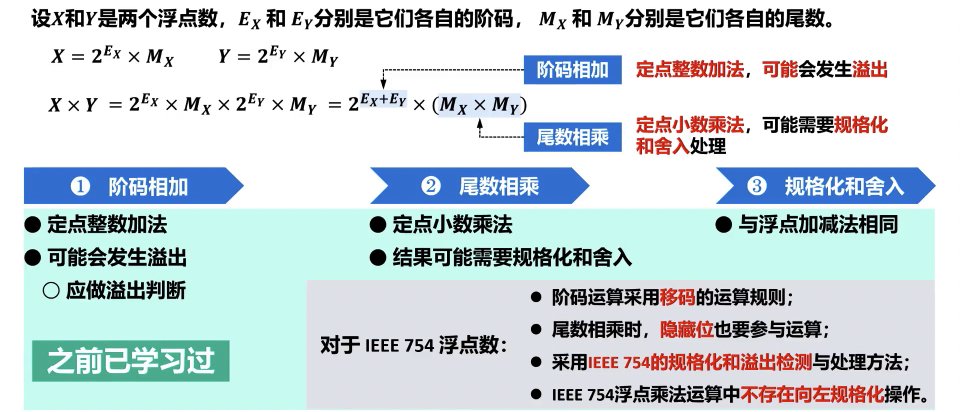
浮点除法运算（仅了解）

• 阶码相减，尾数相除。
• 结果的规格化与舍入。