205 浮点数的表示形式和表示范围

浮点数的表示形式和表示范围

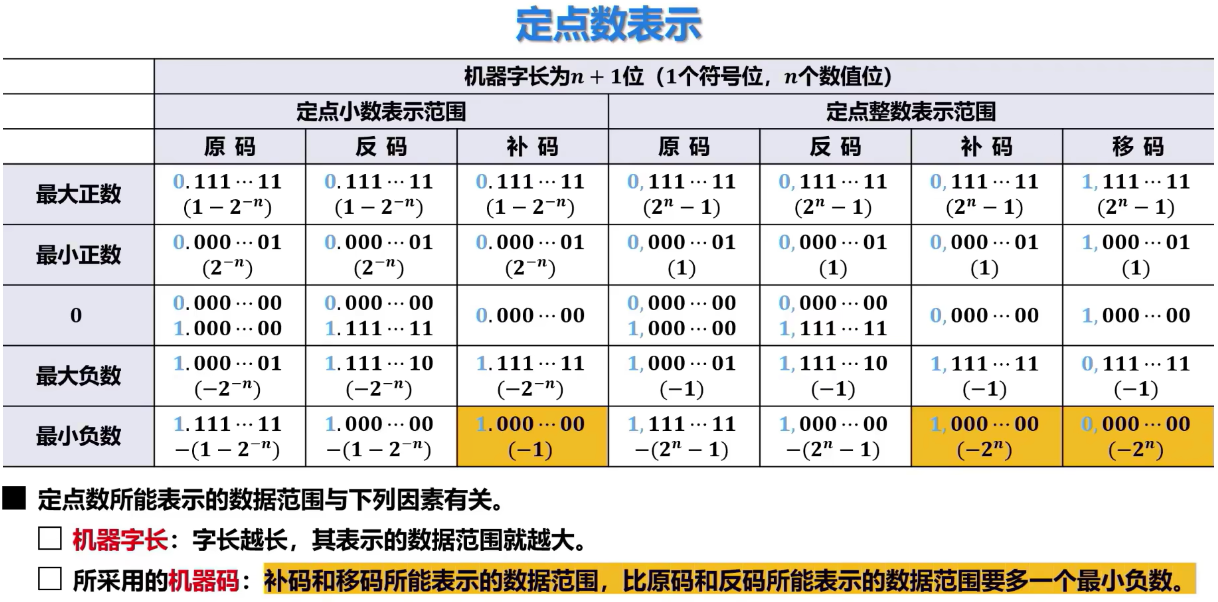
定点数的表示

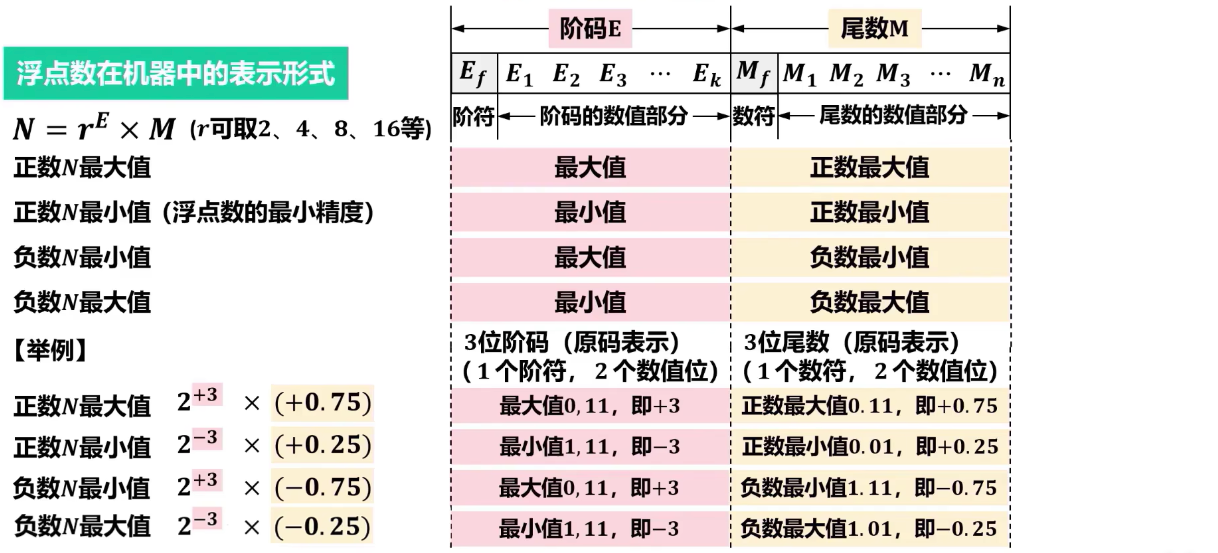
为支持非纯小数或非纯整数的表示，引出浮点数表示形式

浮点数的表示

• 阶码：
  • 阶码的位数决定了数据表示范围
  • 阶码的值决定了小数点的位置
  • 可采用原码、补码、反码、移码表示
• 尾码：
  • 尾码的位数决定了数据表示精度
  • 可采用原码、补码、反码表示

浮点数表示范围

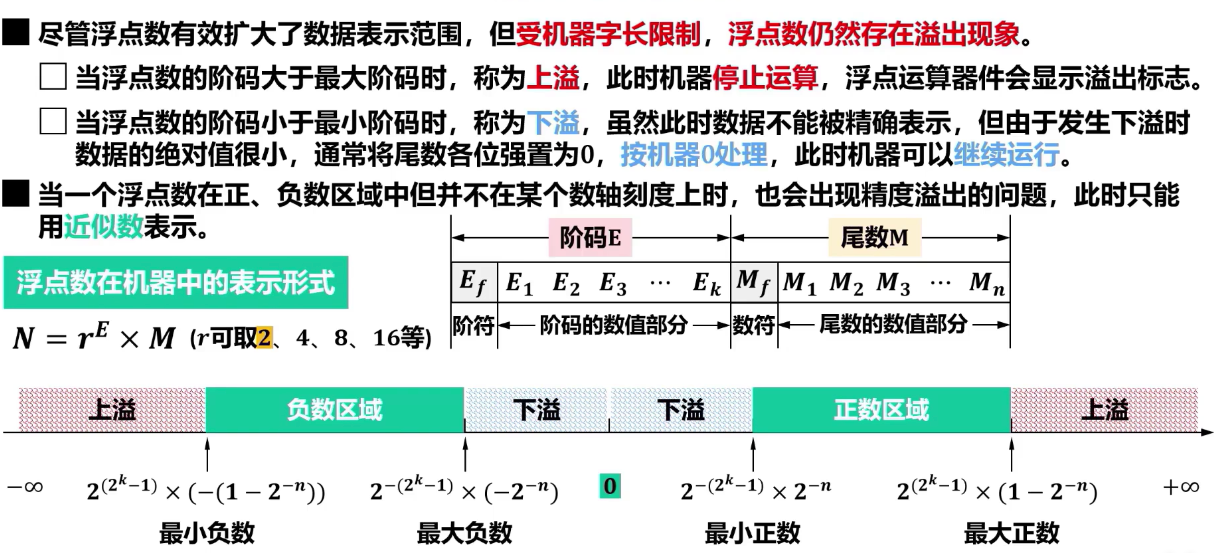
浮点数能有效扩大数据表示范围

• 尽管扩大了范围，但受机器字长限制，浮点数仍存在溢出现象。
  • 上溢 (Overflow)
    • 定义: 当计算结果的绝对值大于浮点数所能表示的最大正数时发生。
    • 原因: 结果的阶码超过了浮点数格式所能表示的最大阶码值。
    • 处理: 在 IEEE 754 标准中，通常将结果表示为正无穷大 (+∞) 或 负无穷大 (-∞)。
  • 下溢 (Underflow)
    • 定义: 当计算结果的绝对值小于浮点数所能表示的最小非零正数时发生。
    • 原因: 结果的阶码小于浮点数格式所能表示的最小阶码值。
    • 处理:
      • 逐渐下溢 (Gradual Underflow)：IEEE 754 标准允许使用非规格化数 (Denormalized Numbers) 来处理。此时尾数不再隐含 1，而是显式地表示，阶码固定为最小值，通过牺牲精度来表示更小的数值，直至 0。
      • 冲刷到零 (Flush to Zero)：某些系统或模式下，直接将过小的非零结果置为零 (0)，导致精度完全丢失。

NOTE

例题 答：阶码和尾数都取最大正数

$$2^{(2^3-1)}\cdot (1-2^{-7})=2^7-1$$