804 选择排序

选择排序

算法思想

选择排序（Selection Sort）的基本思想是：每一趟从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到所有元素排完。

简单选择排序

1. 基本思想：在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
2. 算法过程：
   • 第一趟：从 $n$ 个元素中找到最小（或最大）的元素，将它与第一个元素交换。
   • 第二趟：从剩余的 $n-1$ 个元素中找到最小（或最大）的元素，将它与第二个元素交换。
   • 重复过程：重复上述过程 $n-1$ 趟，直到所有元素都排好序。
3. 性能分析：
   • 时间复杂度：
     • 最好、最坏、平均情况：都是 $O(n^2)$。无论初始序列是否有序，都需要进行 $n-1$ 趟选择，每趟选择都需要比较大约 $n$ 次。
   • 空间复杂度：$O(1)$，因为它只需要常数级别的额外空间来存储临时变量。
   • 稳定性：简单选择排序是不稳定的排序算法。例如，序列 5 8 5 2 9，第一次选择 2 和第一个 5 交换，导致两个 5 的相对位置改变。

堆排序

TIP

注意，计算元素之间比较次数时，除了交换时需要比较，还需比较左右子树谁大（或谁小） 建堆过程，从末尾向前比较

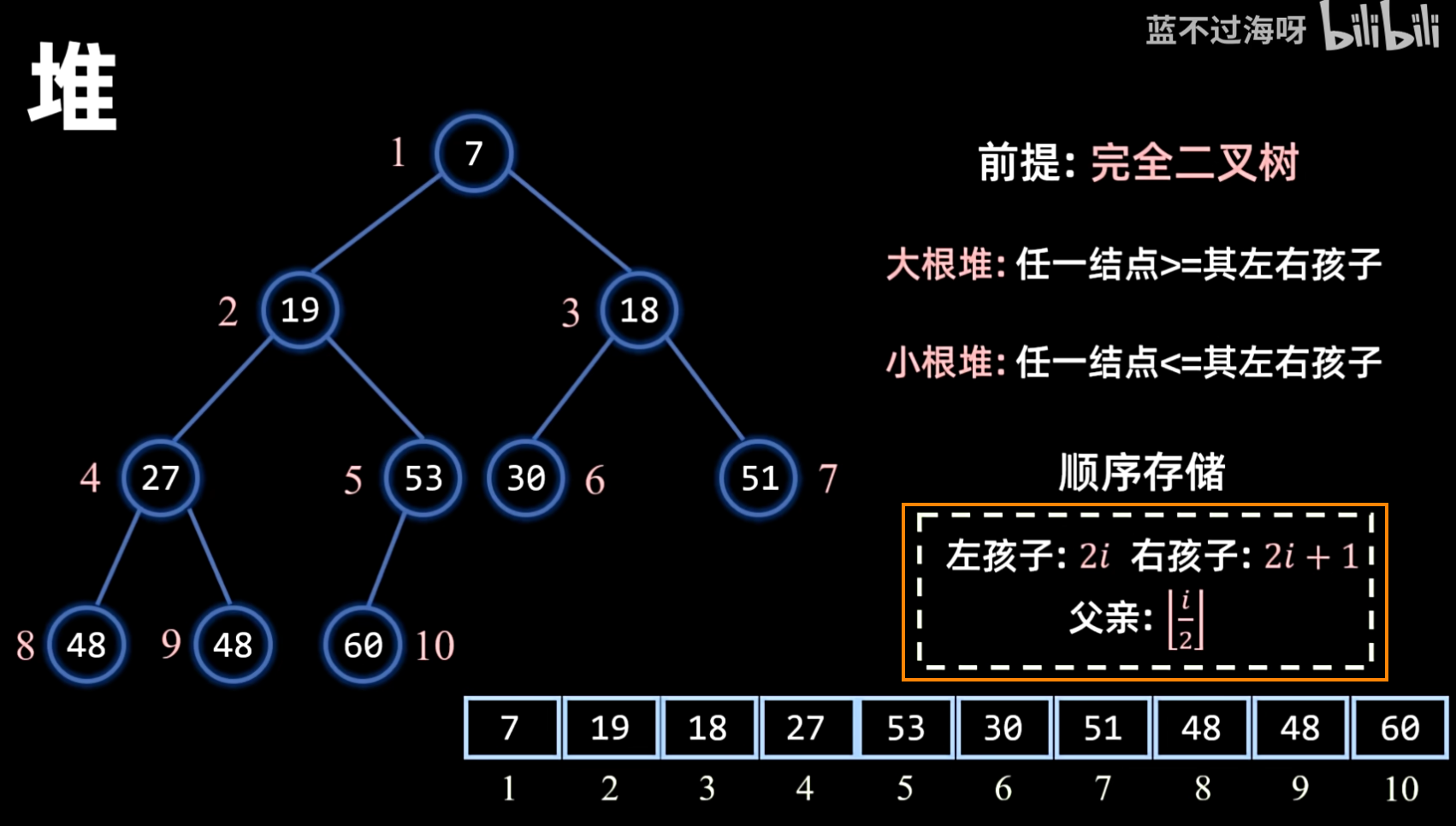
堆排序（Heap Sort）是利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即父节点的键值总是大于等于（或小于等于）其子节点的键值。

完全二叉树

1. 基本思想：将待排序序列构造成一个大顶堆（或小顶堆），此时，整个序列的最大值（或最小值）就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值（或最小值）。然后将剩余 $n-1$ 个元素重新构造成一个堆，这样会得到 $n-1$ 个元素的次大值（或次小值）。重复上述过程，直到整个序列有序。
2. 算法过程：
   • 建堆：将待排序序列构造成一个初始堆（大顶堆或小顶堆）。通常从最后一个非叶子节点开始，自底向上进行调整。
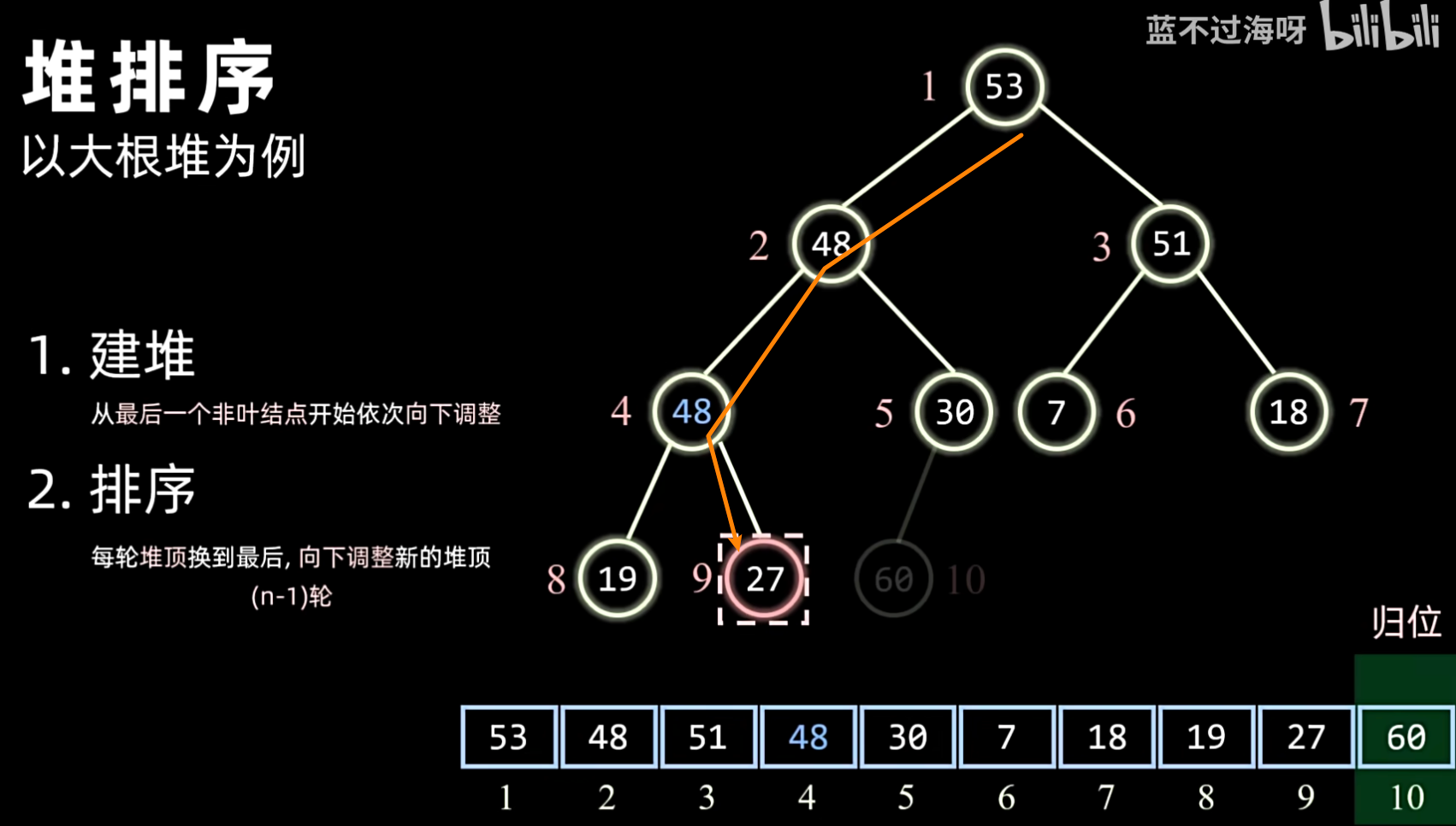
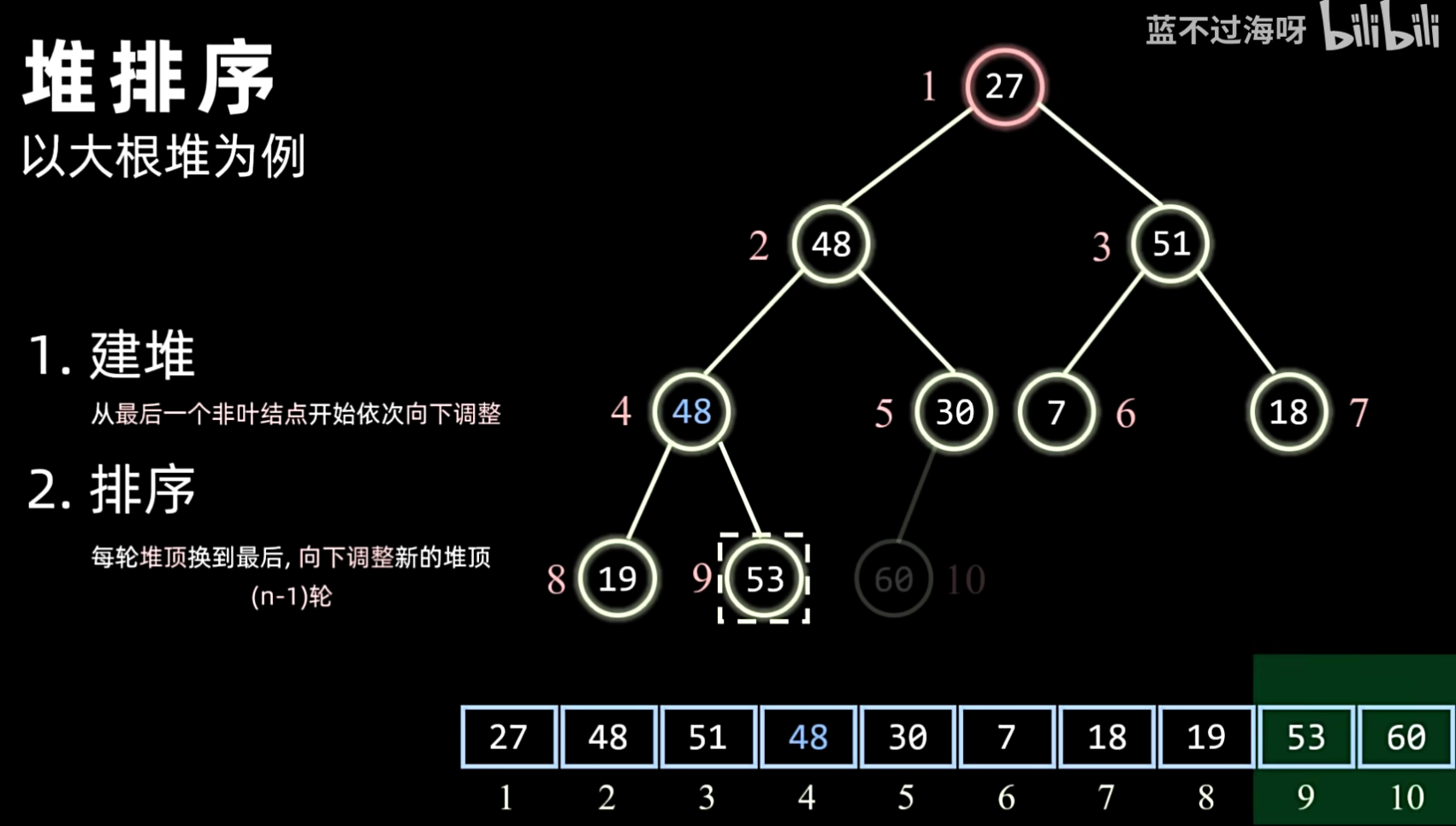
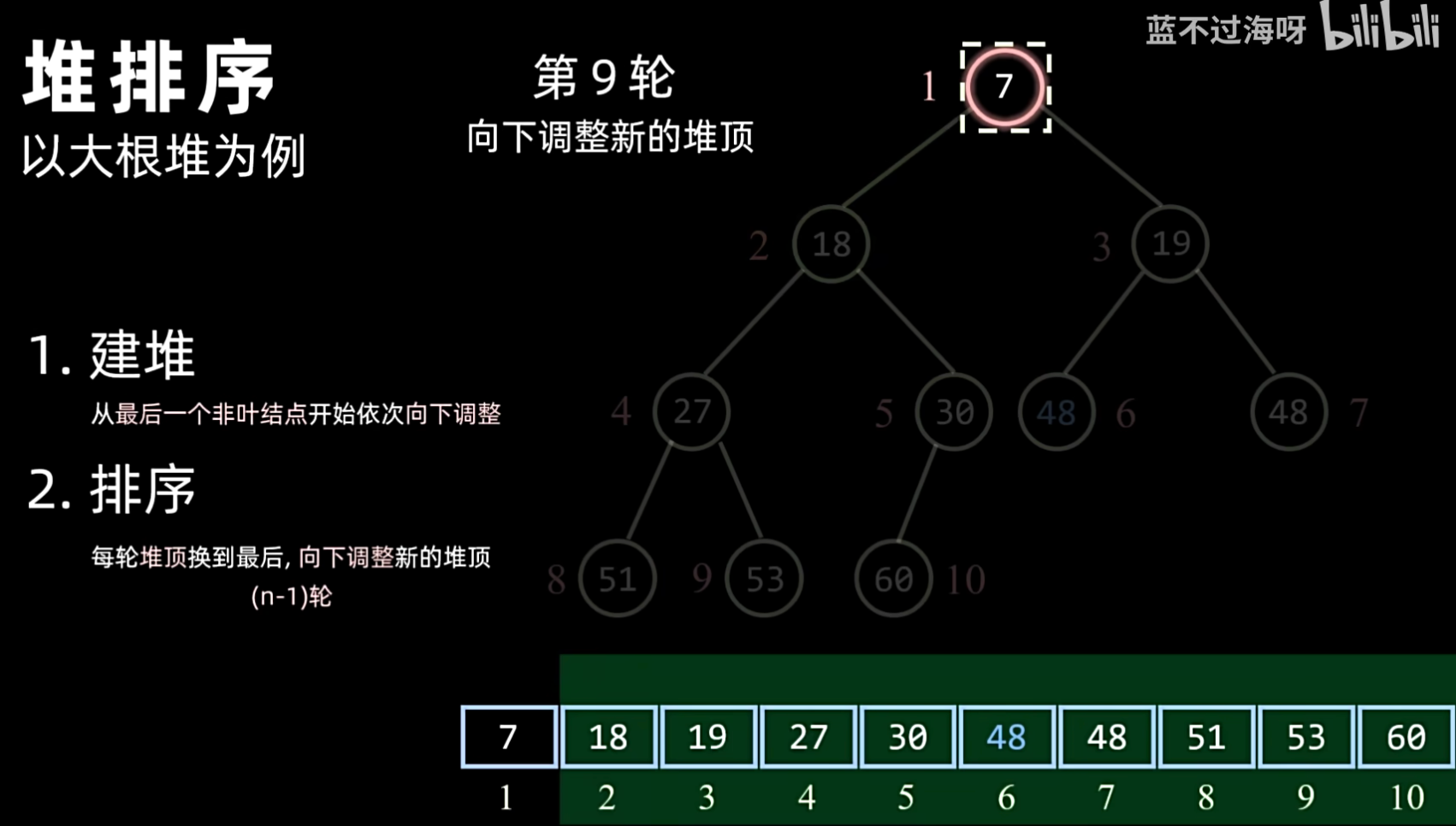
   • 排序：
     • 将堆顶元素（最大或最小）与堆的最后一个元素交换。
     • 交换后，堆的大小减 1。
     • 对新的堆顶元素进行堆化（Sift Down），使其恢复堆的性质。
     • 重复上述步骤，直到堆中只剩一个元素。
3. 性能分析：
   • 时间复杂度：
     • 最好、最坏、平均情况：都是 $O(n\log n)$。建堆的时间复杂度为 $O(n)$，之后有 $n-1$ 次删除堆顶元素和调整堆的操作，每次调整的时间复杂度为 $O(\log n)$。
   • 空间复杂度：$O(1)$，因为它只需要常数级别的额外空间来存储临时变量。
   • 稳定性：堆排序是不稳定的排序算法。在元素下沉过程中，可能会改变相等元素的相对顺序。

建堆操作

建堆（Build Heap）是将一个无序的序列构造成一个满足堆性质的序列。

1. 方法：通常采用 Sift Down（下沉）操作，从最后一个非叶子节点开始，依次向上对其父节点进行堆化。
2. 过程：
   • 对于一个大小为 $n$ 的数组（将其视为完全二叉树），最后一个非叶子节点的索引是 $\lfloor \frac{n}{2}\rfloor -1$。
   • 从该节点开始，逐个向前（递减索引）到根节点（索引 0）。
   • 对每个节点执行 Sift Down 操作：
     • 比较当前节点与其子节点（如果有）。
     • 如果子节点更大（大顶堆）或更小（小顶堆），则与子节点交换。
     • 重复此过程，直到当前节点大于（或小于）其所有子节点，或到达叶子节点。
3. 时间复杂度：$O(n)$。虽然看起来是 $n$ 次 $O(\log n)$ 的操作，但实际上，大部分节点都在树的底部，它们下沉的距离很短，因此总复杂度是线性的。

1. 建堆

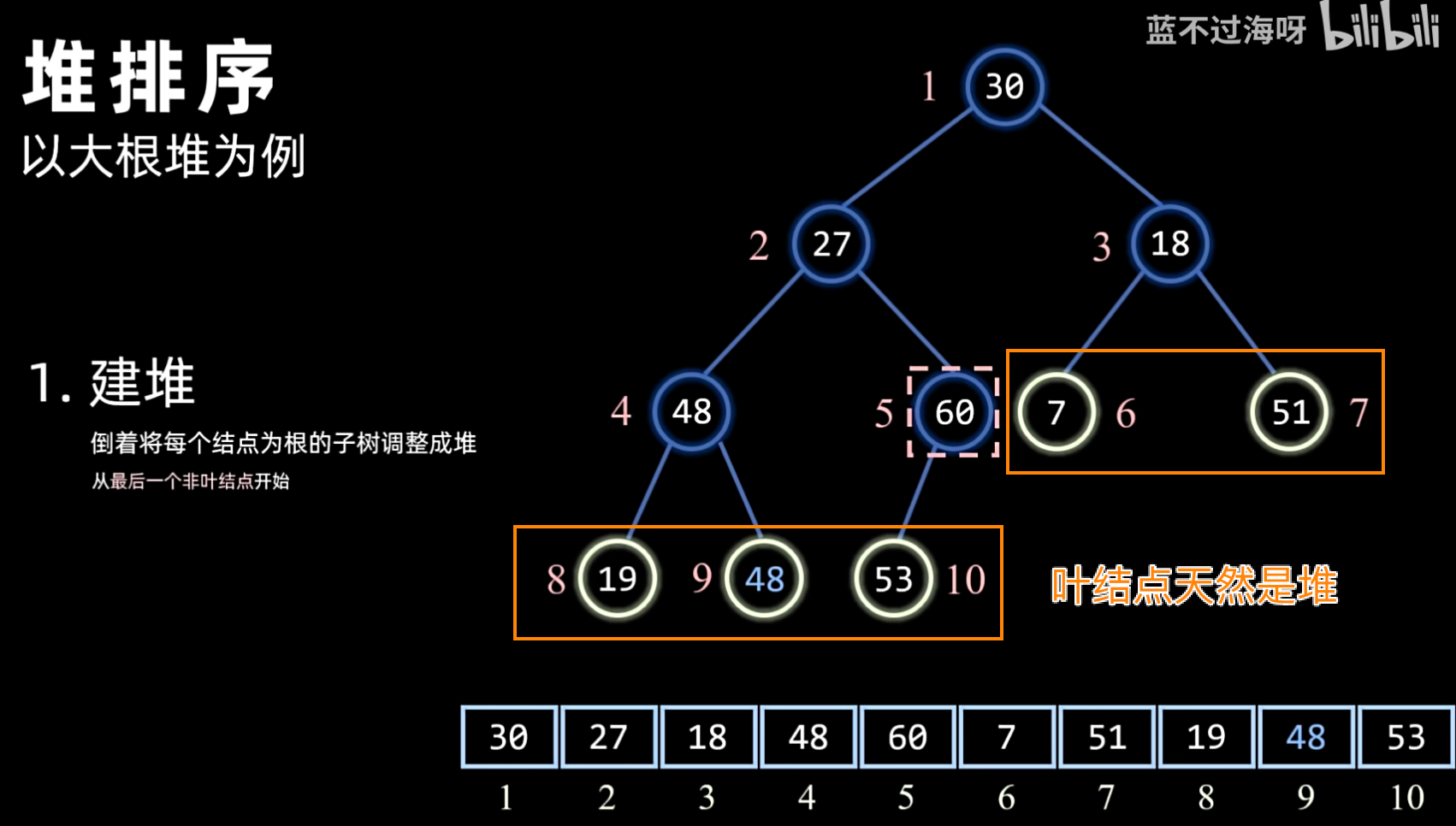
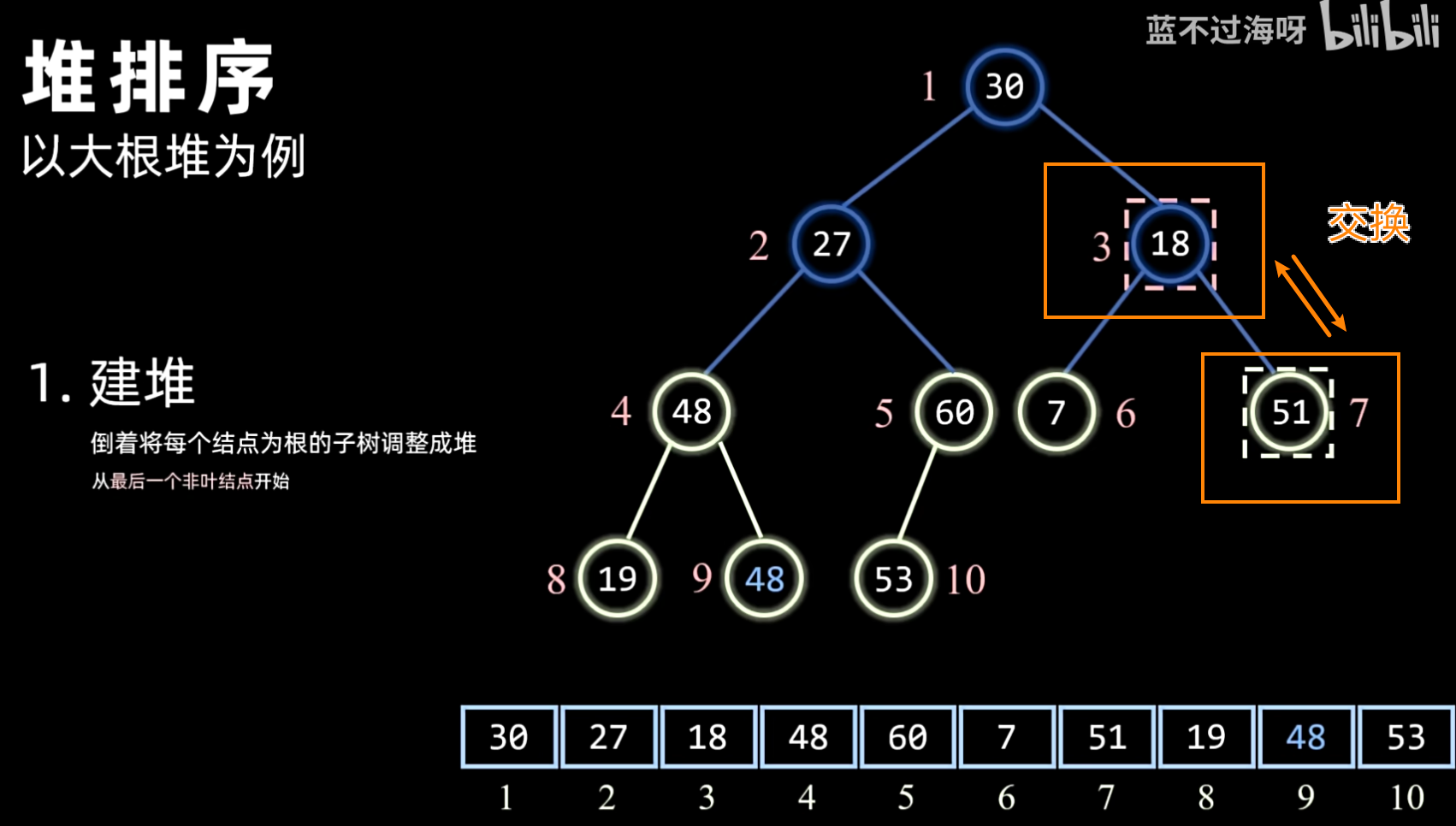
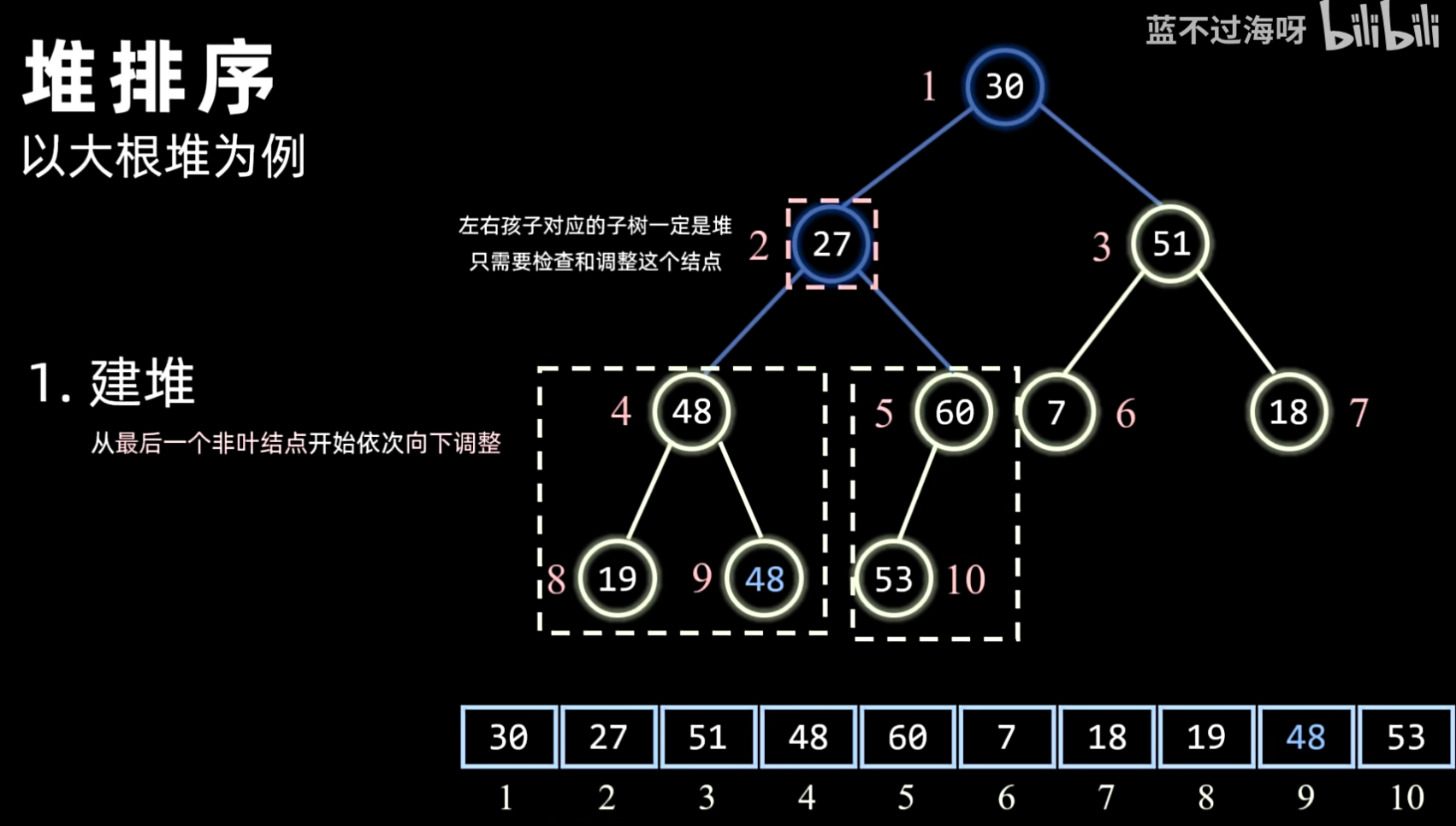
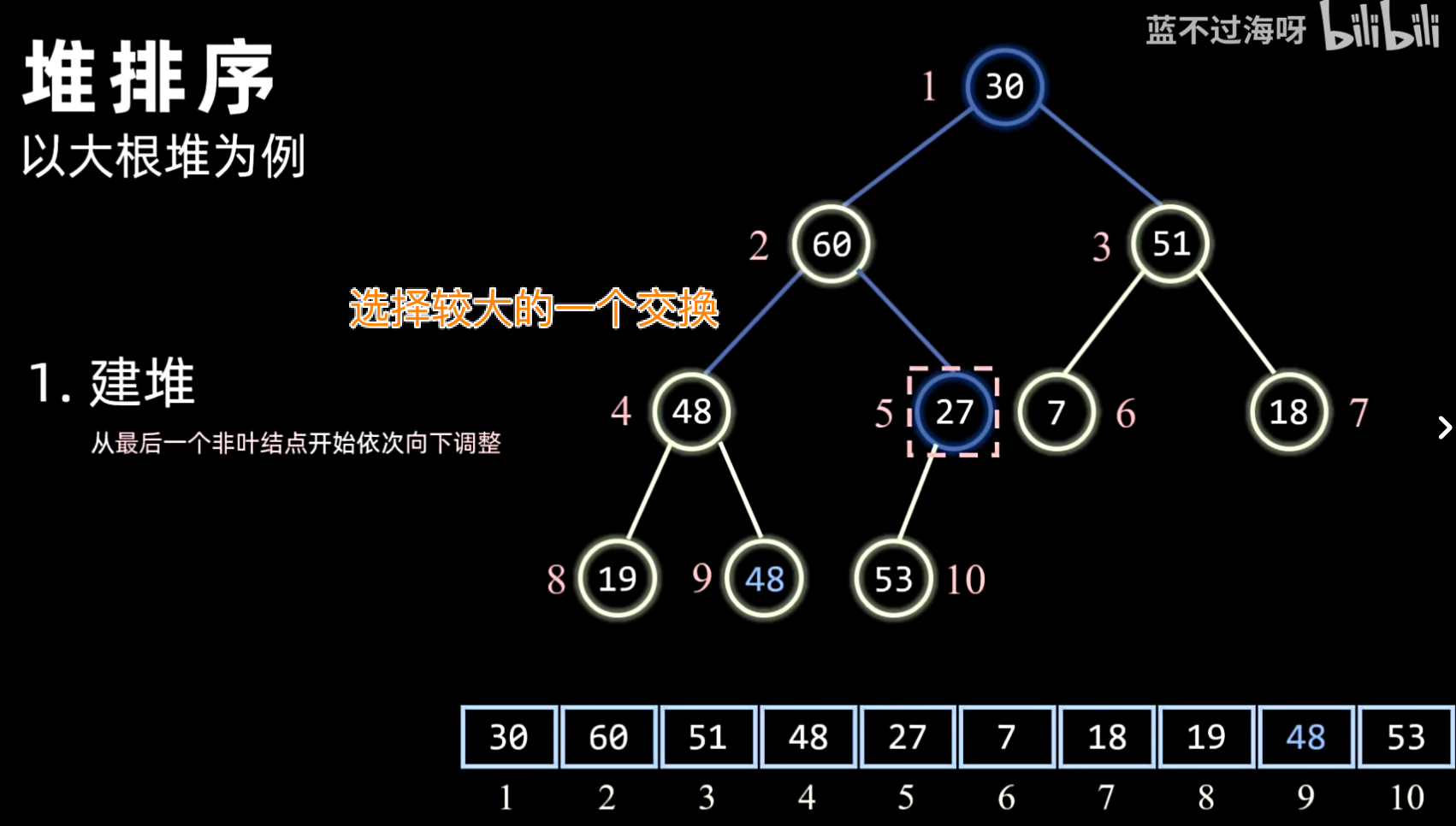
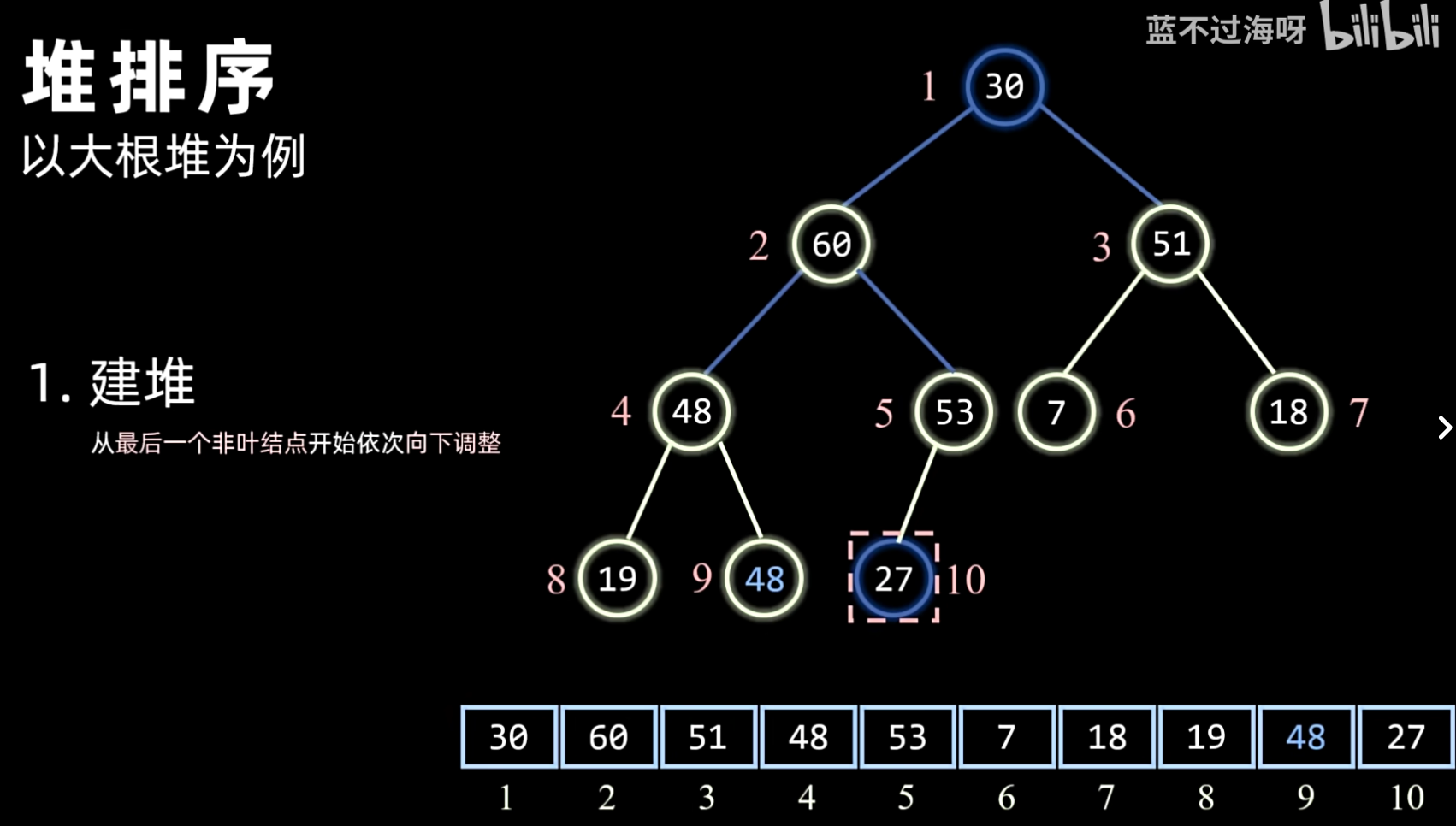
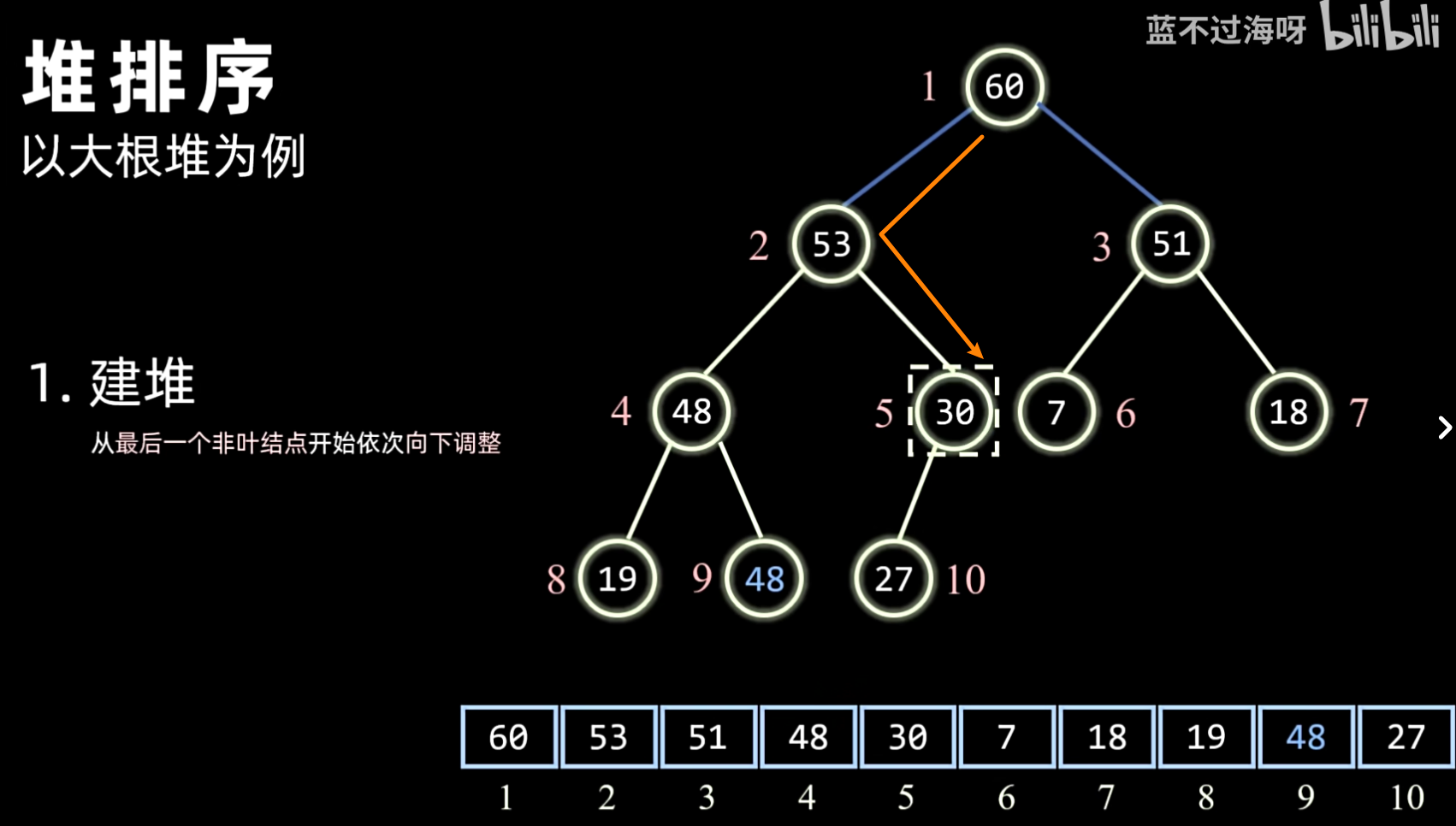
2. 排序

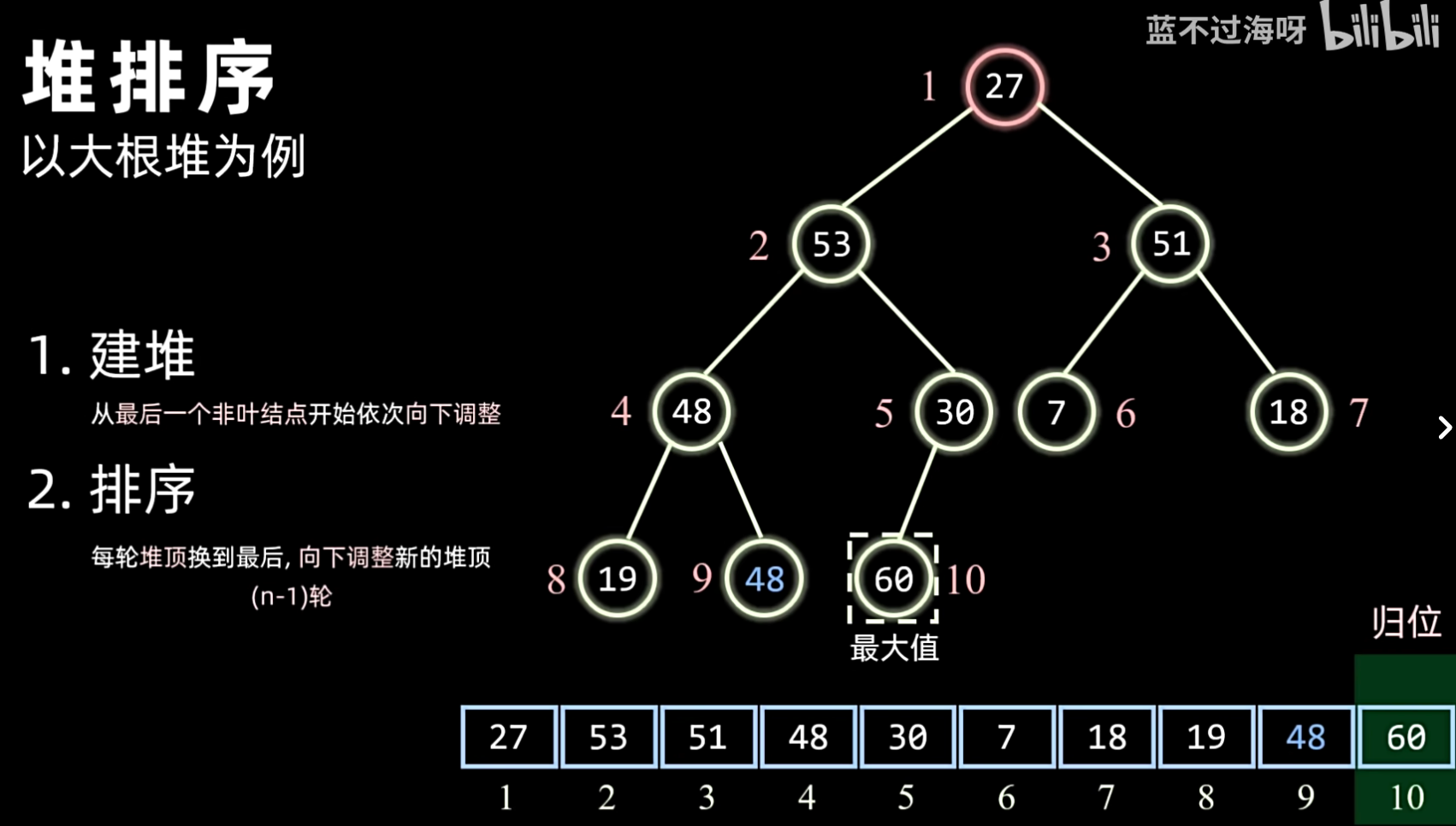
堆的删除及调整

删除堆顶元素是堆排序的核心操作之一。

1. 删除操作：
   • 对于大顶堆，删除的是最大元素（堆顶元素）。
   • 将堆顶元素与堆的最后一个元素交换。
   • 堆的大小减 1。
   • 对新的堆顶元素执行 Sift Down（下沉）操作，使其恢复堆的性质。
2. 调整（Sift Down）过程：
   • 设当前需要调整的节点为 current。
   • 找到 current 的子节点中最大（大顶堆）或最小（小顶堆）的那个。
   • 如果 current 小于（大顶堆）或大于（小顶堆）其最大（最小）子节点，则交换它们。
   • 将 current 更新为交换后的子节点位置，并继续向下调整，直到 current 大于（或小于）其所有子节点，或 current 成为叶子节点。
3. 时间复杂度：$O(\log n)$，因为调整过程是从根（或某个节点）到叶子的路径，路径长度为树的高度，即 $\log n$。

堆的插入及调整

在堆中插入一个新元素。

1. 插入操作：
   • 将新元素添加到堆的末尾（数组的最后一个位置）。
   • 对新插入的元素执行 Sift Up（上浮）操作，使其恢复堆的性质。
2. 调整（Sift Up）过程：
   • 设当前需要调整的节点为 current（新插入的元素）。
   • 比较 current 与其父节点。
   • 如果 current 大于（大顶堆）或小于（小顶堆）其父节点，则交换它们。
   • 将 current 更新为交换后的父节点位置，并继续向上调整，直到 current 小于（或大于）其父节点，或 current 成为根节点。
3. 时间复杂度：$O(\log n)$，因为调整过程是从叶子（或某个节点）到根的路径，路径长度为树的高度，即 $\log n$。

选取最小 k 个数的应用和效率分析

堆排序思想在“选取最小 k 个数”或“Top K 问题”中有广泛应用。

1. 应用场景：从海量数据中找出最大的 K 个元素，或最小的 K 个元素。
2. 实现方法：
   • 方法一（大顶堆）：
     • 构建一个大小为 K 的小顶堆。
     • 遍历所有元素：
       • 如果当前元素小于堆顶元素，则替换堆顶元素，并进行堆调整（Sift Down）。
       • 如果当前元素大于或等于堆顶元素，则忽略。
     • 遍历结束后，小顶堆中的 K 个元素即为原序列中最小的 K 个数。
   • 方法二（小顶堆）：
     • 构建一个大小为 K 的大顶堆。
     • 遍历所有元素：
       • 如果当前元素大于堆顶元素，则替换堆顶元素，并进行堆调整（Sift Down）。
       • 如果当前元素小于或等于堆顶元素，则忽略。
     • 遍历结束后，大顶堆中的 K 个元素即为原序列中最大的 K 个数。
3. 效率分析：
   • 时间复杂度：
     • 建堆：$O(K)$。
     • 遍历剩余 $N-K$ 个元素，每次操作 $O(\log K)$。
     • 总时间复杂度：$O(K+(N-K)\log K)=O(N\log K)$。
   • 空间复杂度：$O(K)$，用于存储 K 个元素的堆。
4. 优点：
   • 相比于完全排序整个数组（$O(N\log N)$），当 K 远小于 N 时，效率更高。
   • 适用于处理海量数据，因为不需要一次性将所有数据加载到内存中。