交换排序
算法思想
交换排序的基本思想是:通过比较待排序序列中两个元素的关键字,如果它们的顺序不符合要求,就交换它们的位置,直到整个序列达到有序状态。
冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法。
- 基本思想:它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复进行的,直到没有再需要交换,也就是说该数列已经排序完成。
- 算法过程:
- 一趟冒泡:从序列的第一个元素开始,依次比较相邻的两个元素。如果前一个元素大于后一个元素,则交换它们的位置。这样,每一趟冒泡都会将当前未排序序列中最大的元素“冒泡”到其最终位置。
- 重复过程:重复上述过程 趟(对于一个长度为 的序列),直到所有元素都排好序。
- 性能分析:
- 时间复杂度:
- 最好情况(序列已经有序):。此时,第一趟冒泡时没有发生任何交换,算法可以提前终止。
- 最坏情况(序列逆序):。需要进行 趟冒泡,每趟比较和交换的次数大致为 。
- 平均情况:。
- 空间复杂度:,因为它只需要常数级别的额外空间来存储临时变量。
- 稳定性:冒泡排序是稳定的排序算法。如果两个元素的关键字相等,它们相对位置不会改变。
- 时间复杂度:
快速排序
快速排序(Quick Sort)是一种高效的排序算法,基于分治策略。
- 基本思想:
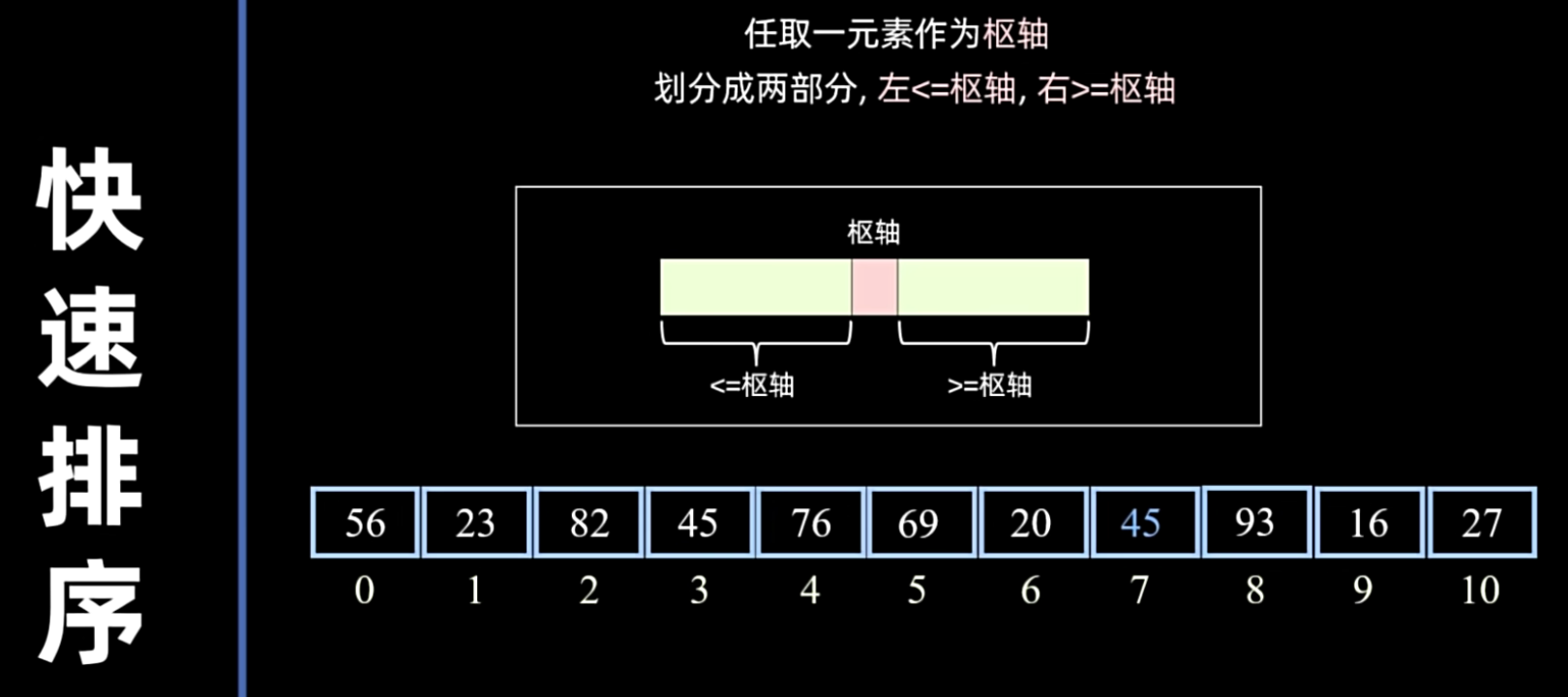
- 选择基准(Pivot):从待排序序列中选择一个元素作为“基准”(pivot)。
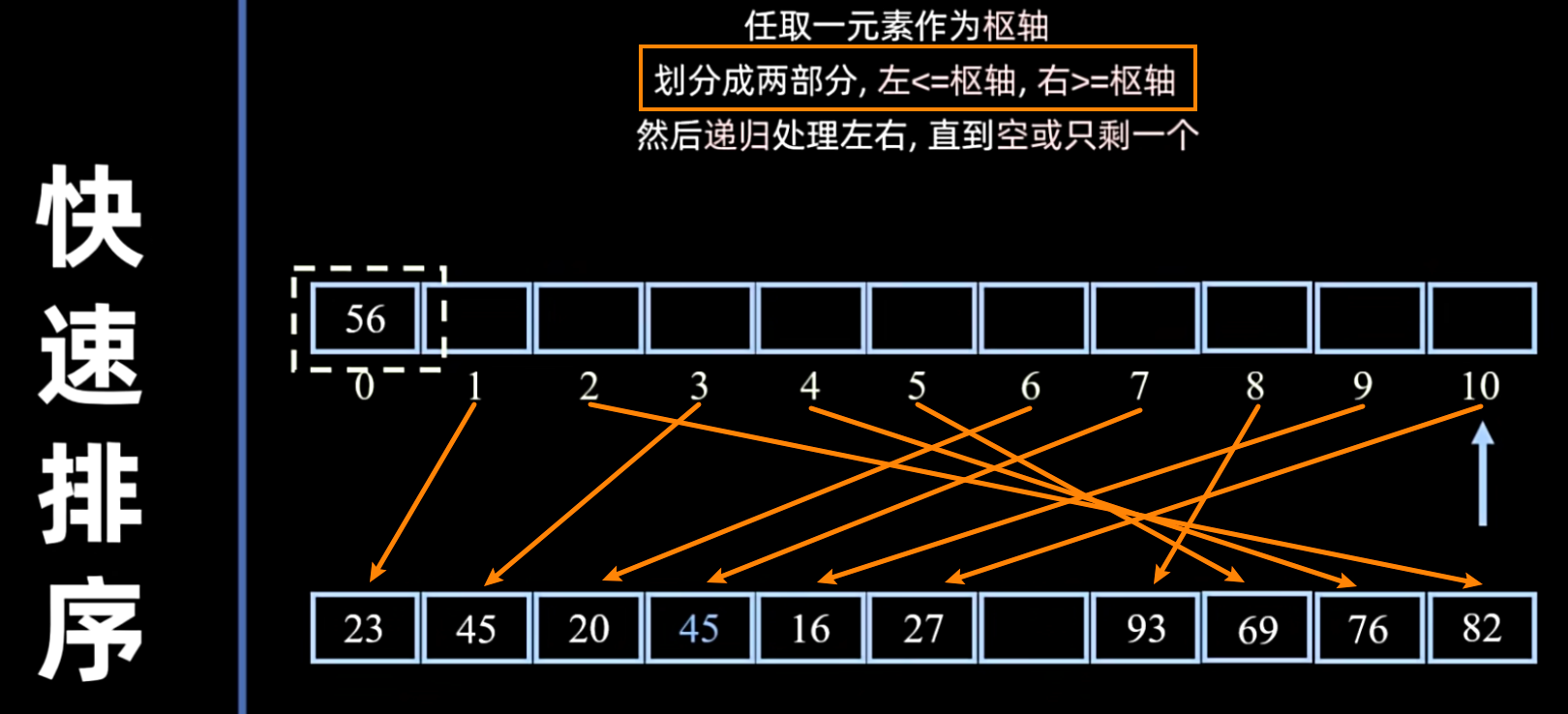
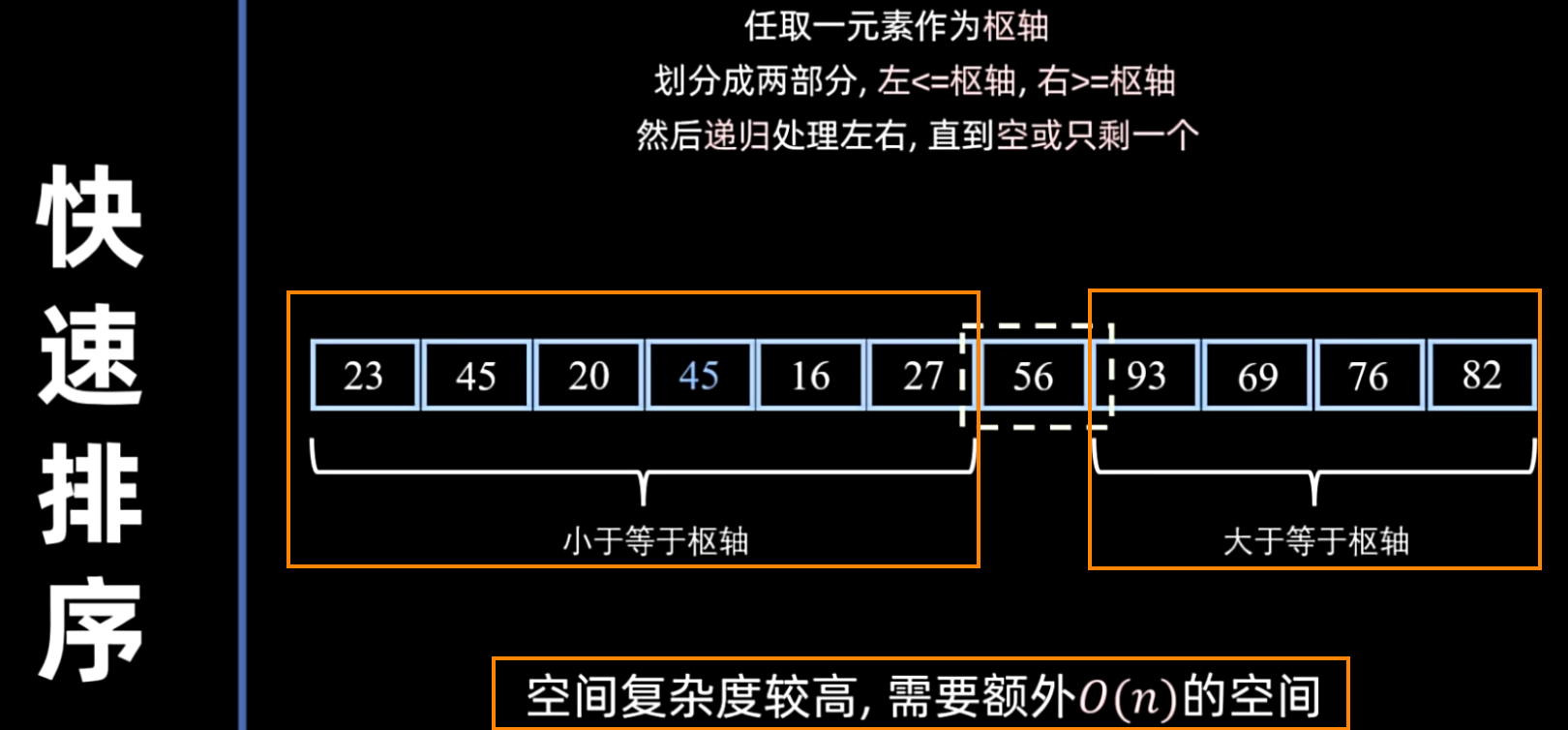
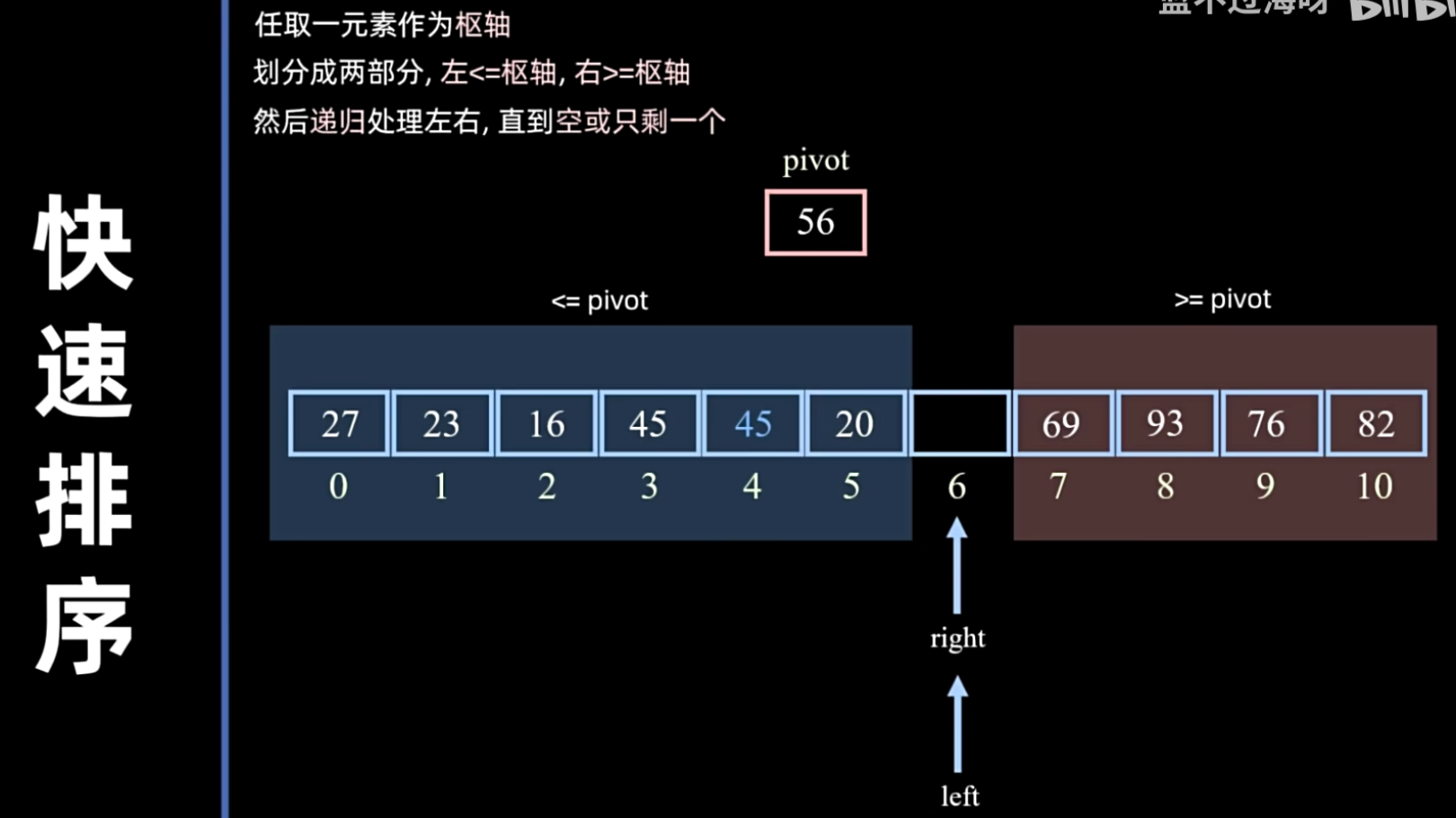
- 划分(Partition):重新排序序列,将所有比基准值小的元素放在基准前面,所有比基准值大的元素放在基准后面(相等的可以放在任意一边)。在这个划分结束之后,该基准就处于其最终的正确位置上。
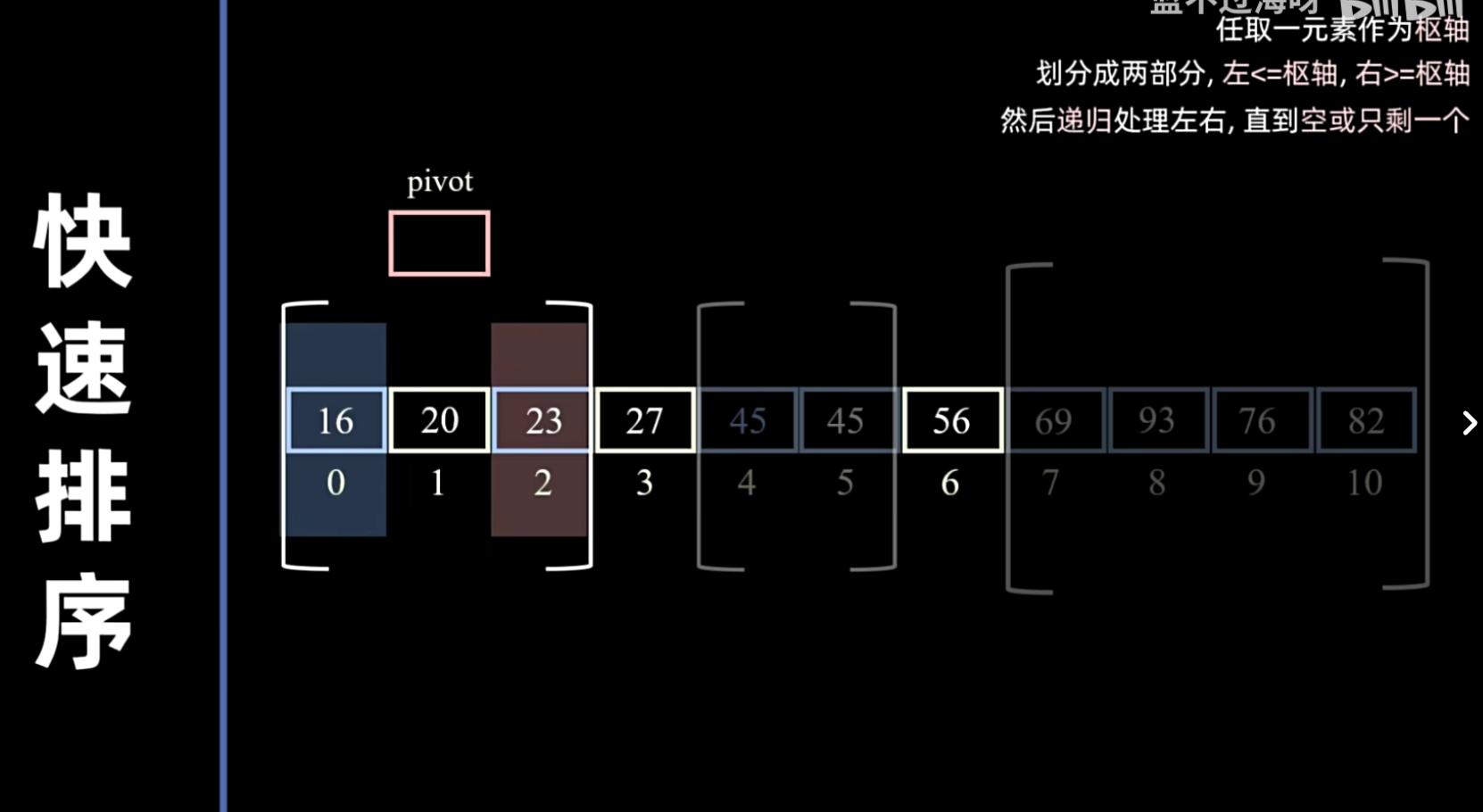
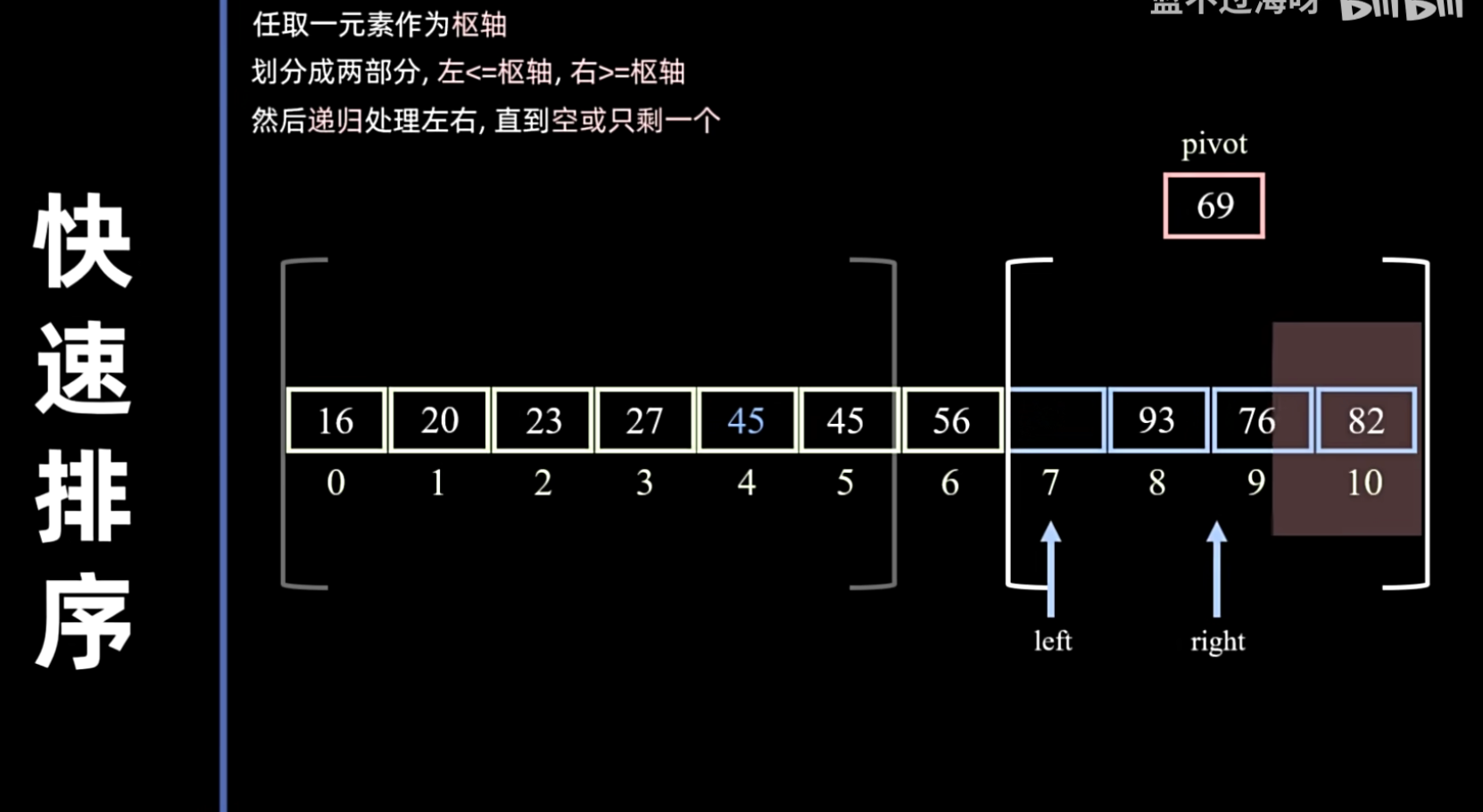
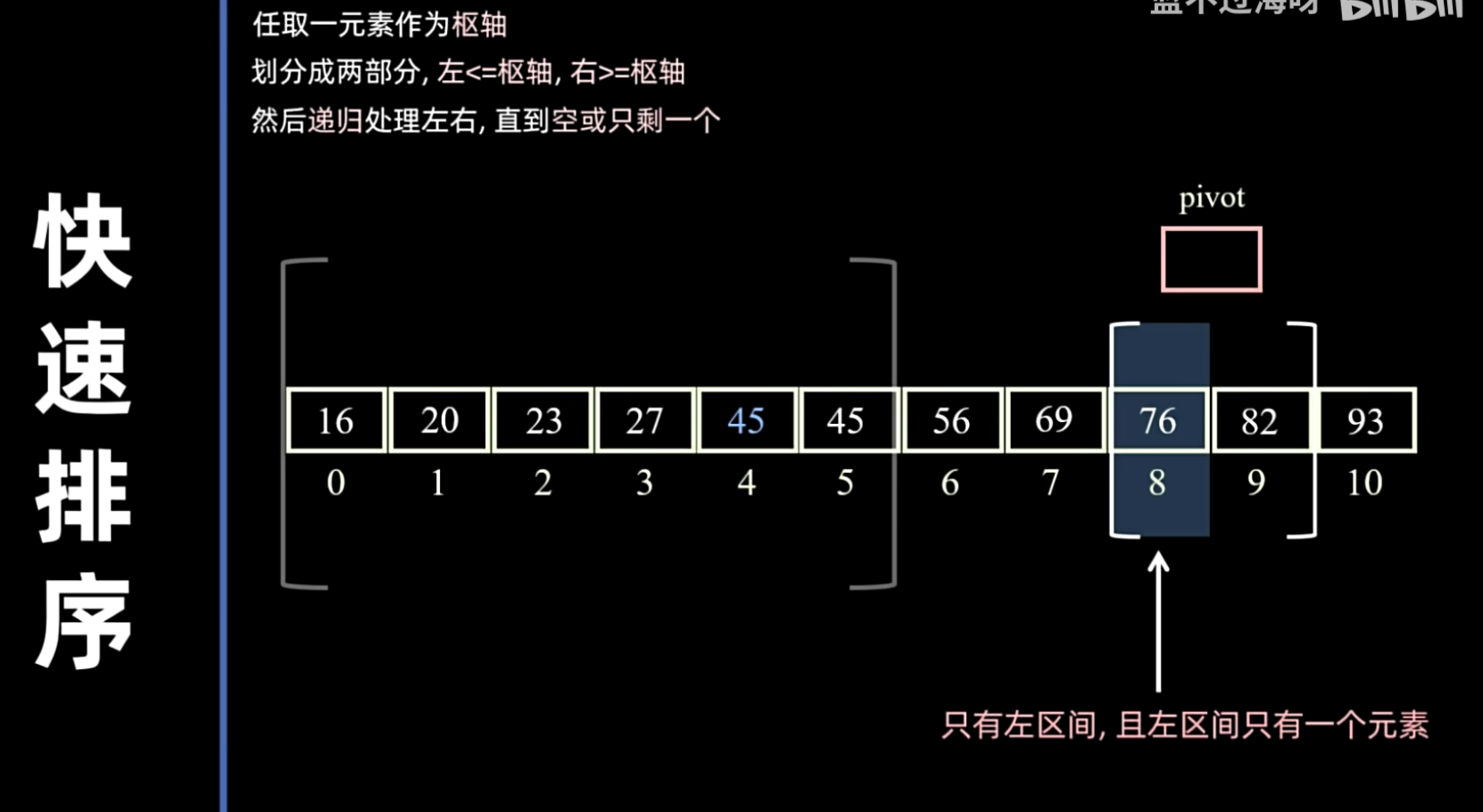
- 递归:递归地对基准值前和基准值后的两个子序列进行快速排序。
- 算法过程:
- 选择基准元素:通常选择序列的第一个、最后一个或中间元素作为基准。也可以随机选择。
- 划分操作:
- 设基准值为
pivot。 - 使用两个指针
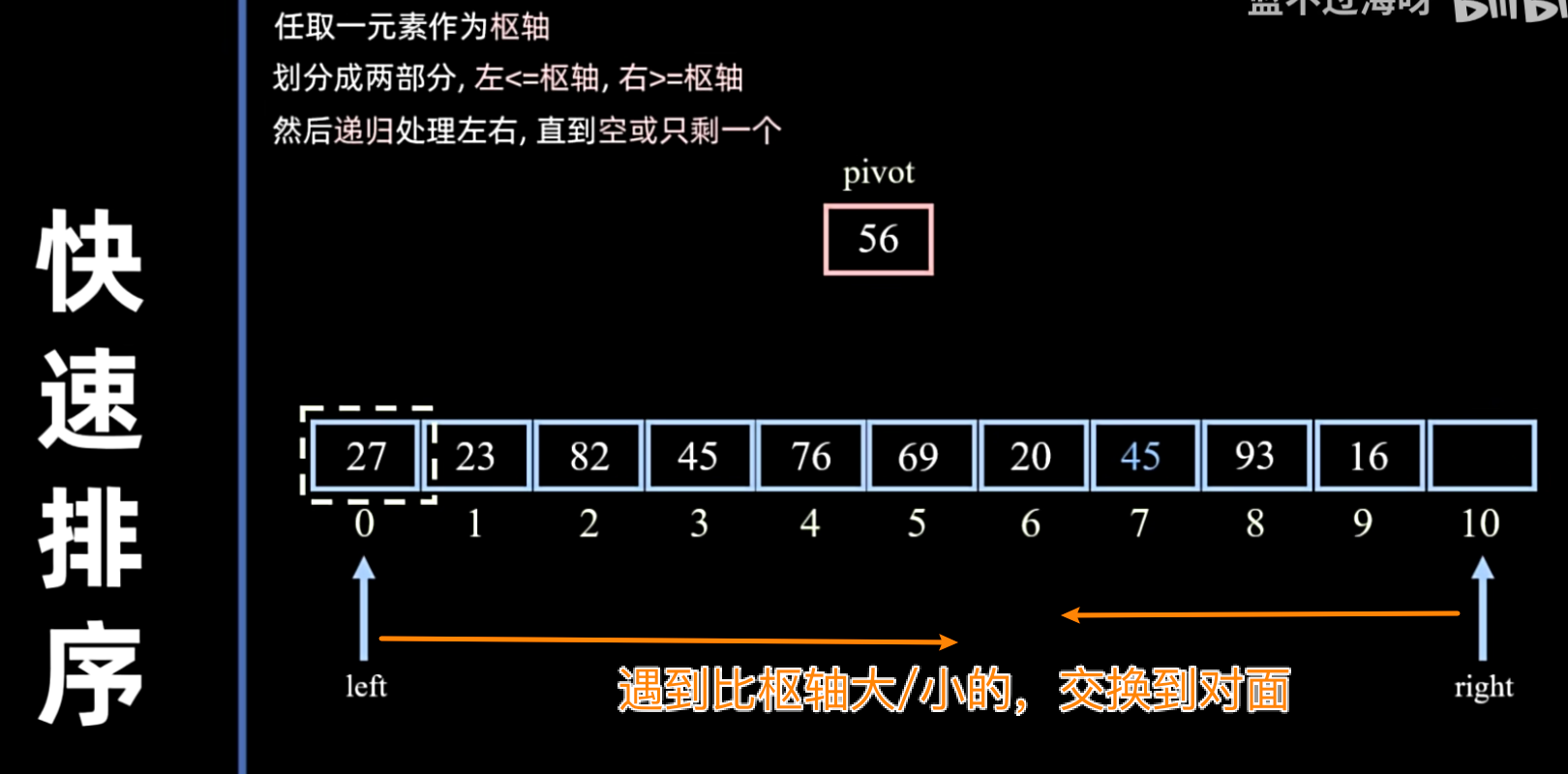
i和j,i从左向右扫描,j从右向左扫描。 i找到第一个大于pivot的元素,j找到第一个小于pivot的元素。- 交换
arr[i]和arr[j]。 - 当
i和j相遇时,将pivot放到i和j相遇的位置。
- 设基准值为
- 递归调用:对基准元素左右两边的子序列重复上述过程。
- 性能分析:
- 时间复杂度:
- 最好情况(每次划分都将序列均匀分成两部分):。例如,每次都选择中位数作为基准。
- 最坏情况(每次划分都产生一个空子序列和一个 长度的子序列,例如序列已经有序或逆序,且选择第一个/最后一个元素作为基准):。
- 平均情况:。
- 空间复杂度:(平均情况)到 (最坏情况),取决于递归深度,通常是栈空间消耗。
- 稳定性:快速排序是不稳定的排序算法。在划分过程中,可能会交换相等元素的相对位置。
- 时间复杂度:
采用 O(n) 空间的快排
采用 O(1) 空间的快排
递归地处理两个子区间
效率分析
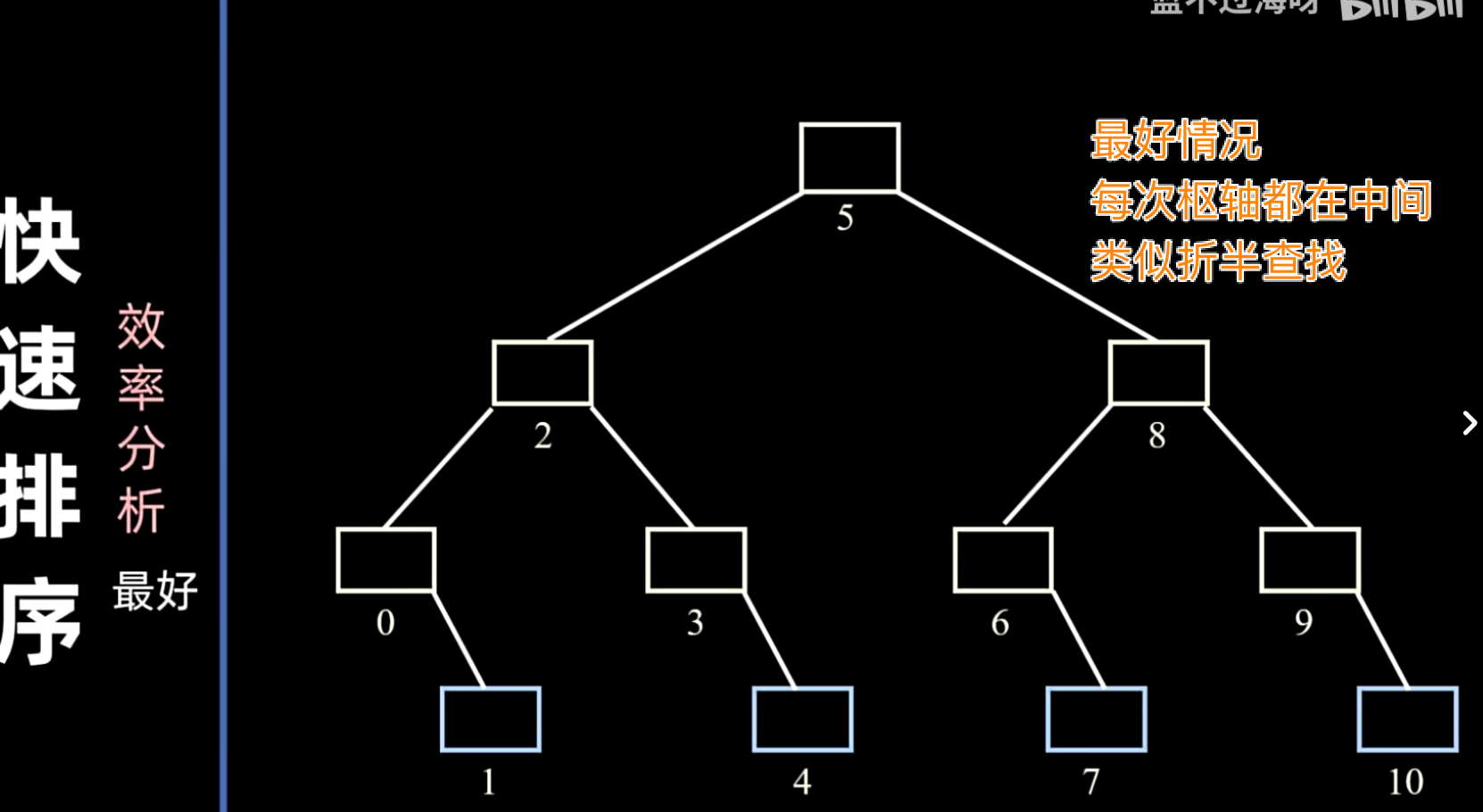
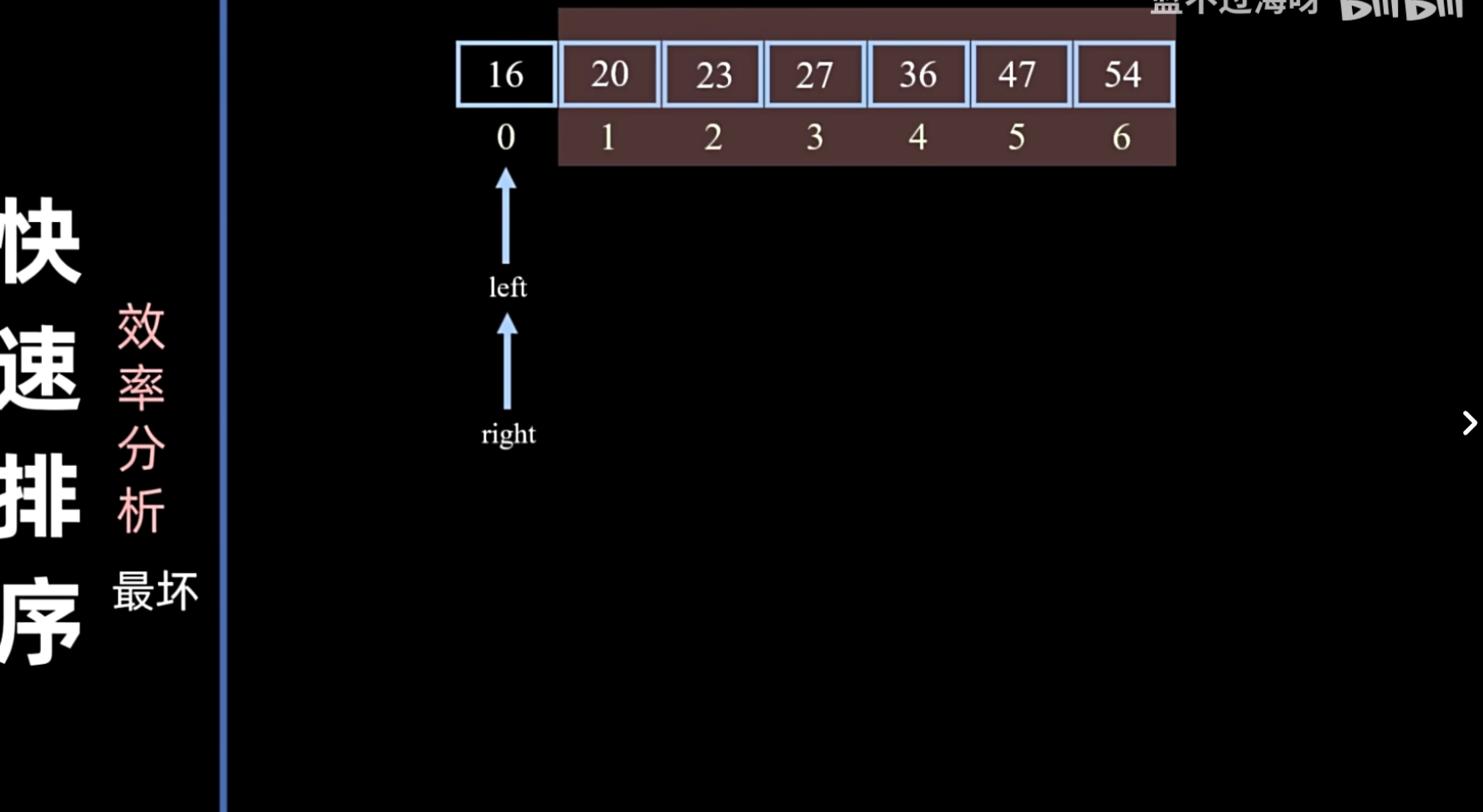
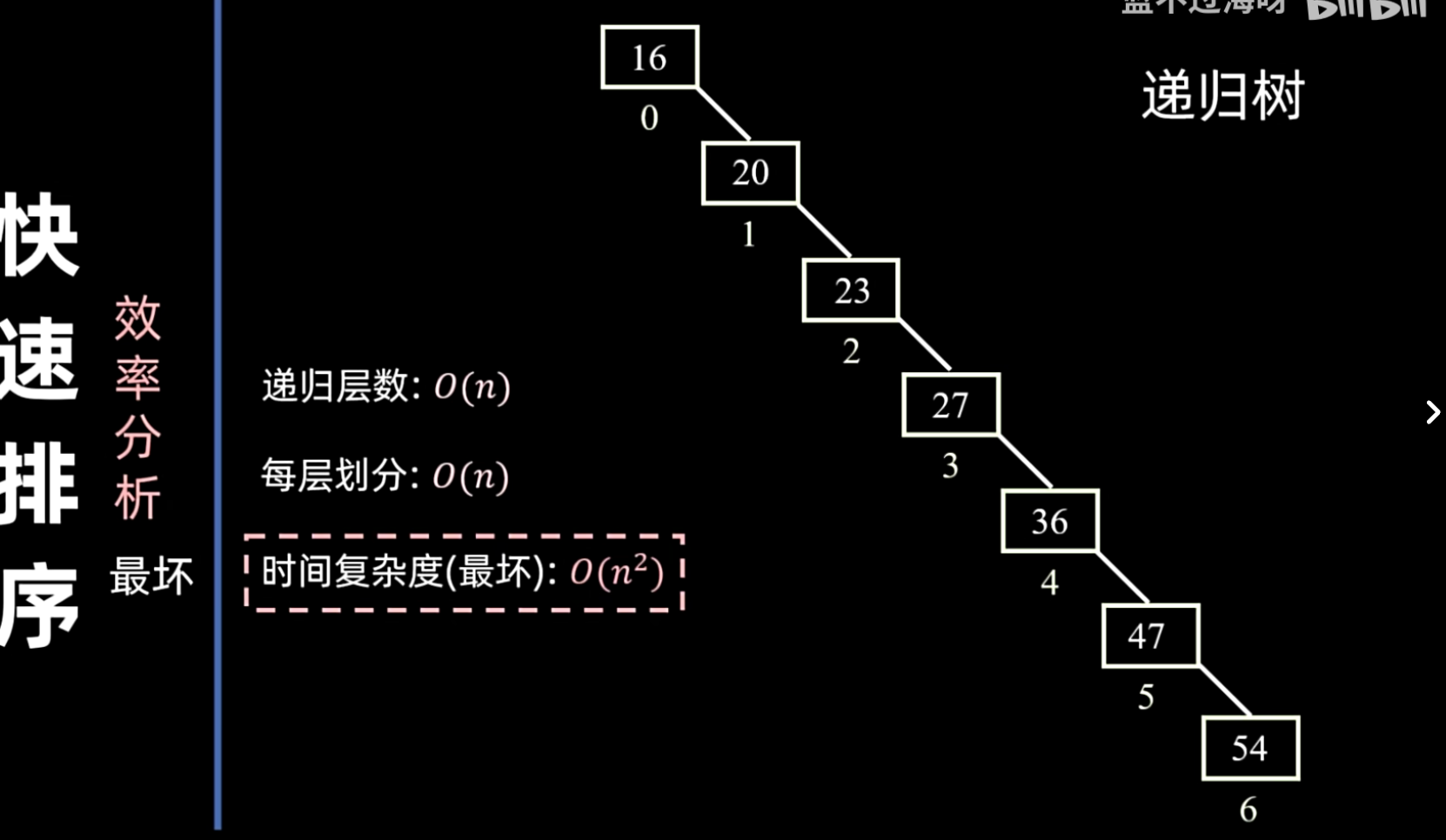
划分操作对性能的影响
划分操作是快速排序的核心,其效率直接影响整个算法的性能。
- 基准选择:
- 固定选择(如选择第一个或最后一个元素):在输入序列部分有序或完全有序时,可能导致划分不均匀,退化为最坏情况 。
- 随机选择:可以有效避免最坏情况的发生,使平均性能保持在 。
- 三数取中法:选择序列的第一个、中间和最后一个元素的中位数作为基准。这种方法可以提高划分的均匀性,减少出现最坏情况的概率。
- 划分过程:
- 双指针法:常用的划分方法,通过两个指针从两端向中间扫描并交换元素,效率较高。
- 单指针法(Hoare Partition Scheme 或 Lomuto Partition Scheme):也可以实现划分,但双指针法通常被认为更健壮,且在某些情况下能更好地处理重复元素。
- 划分均匀性:
- 理想的划分是将序列分成大小相等的两部分。
- 划分越不均匀,递归深度越大,算法性能越接近 。
- 划分越均匀,递归深度越小,算法性能越接近 。
- 重复元素处理:
- 如果序列中包含大量重复元素,传统的划分方法可能导致划分不均匀(例如,所有重复元素都分到一边),从而降低效率。
- 三向切分(Dutch National Flag Problem):一种改进的快速排序,将序列划分为小于基准、等于基准和大于基准的三个部分。这对于包含大量重复元素的序列能显著提高性能,避免了对相等元素的重复处理,使算法在处理相同元素时效率更高。
- 这种方法将时间复杂度降至 对于包含大量重复元素的序列。
- 小规模子序列处理:
- 当子序列的长度较小(例如小于 10-20 个元素)时,快速排序的递归开销可能大于简单的排序算法(如插入排序)。
- 优化方法是当子序列长度达到一定阈值时,停止快速排序的递归,转而使用插入排序对这些小规模子序列进行排序。这种混合排序策略可以提高整体性能。