归并排序、基数排序和计数排序
归并排序
- 算法思想:
- 归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
- 分:将含有 个元素的序列不断地分解成两个子序列,直到每个子序列只包含一个元素(一个元素被认为是自然有序的)。
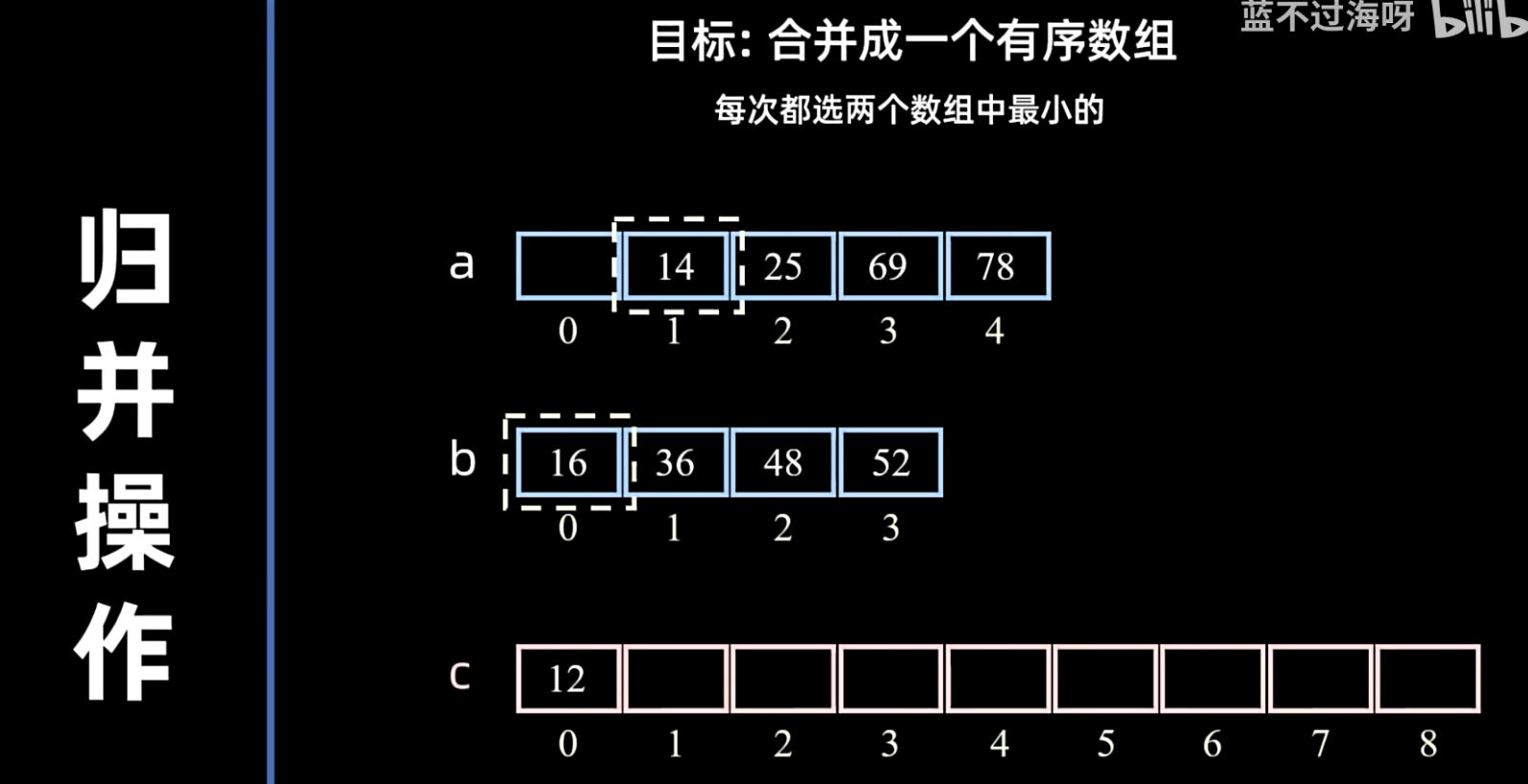
- 治:将分解的子序列两两合并(归并),每次合并都使子序列有序,直到最终合并成一个完整的有序序列。
- 算法过程:
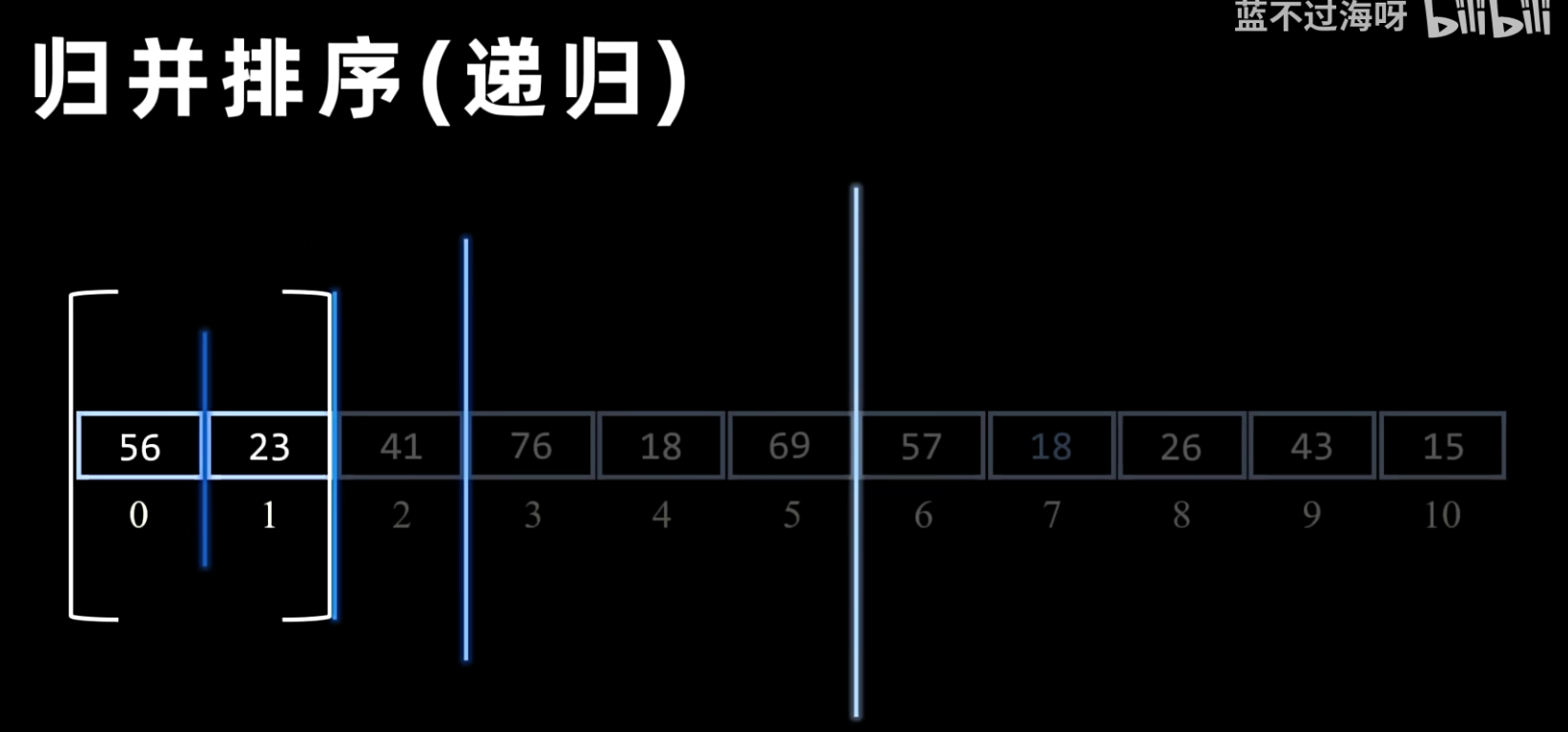
- 分解:递归地将当前序列一分为二,直到每个子序列只包含一个元素。
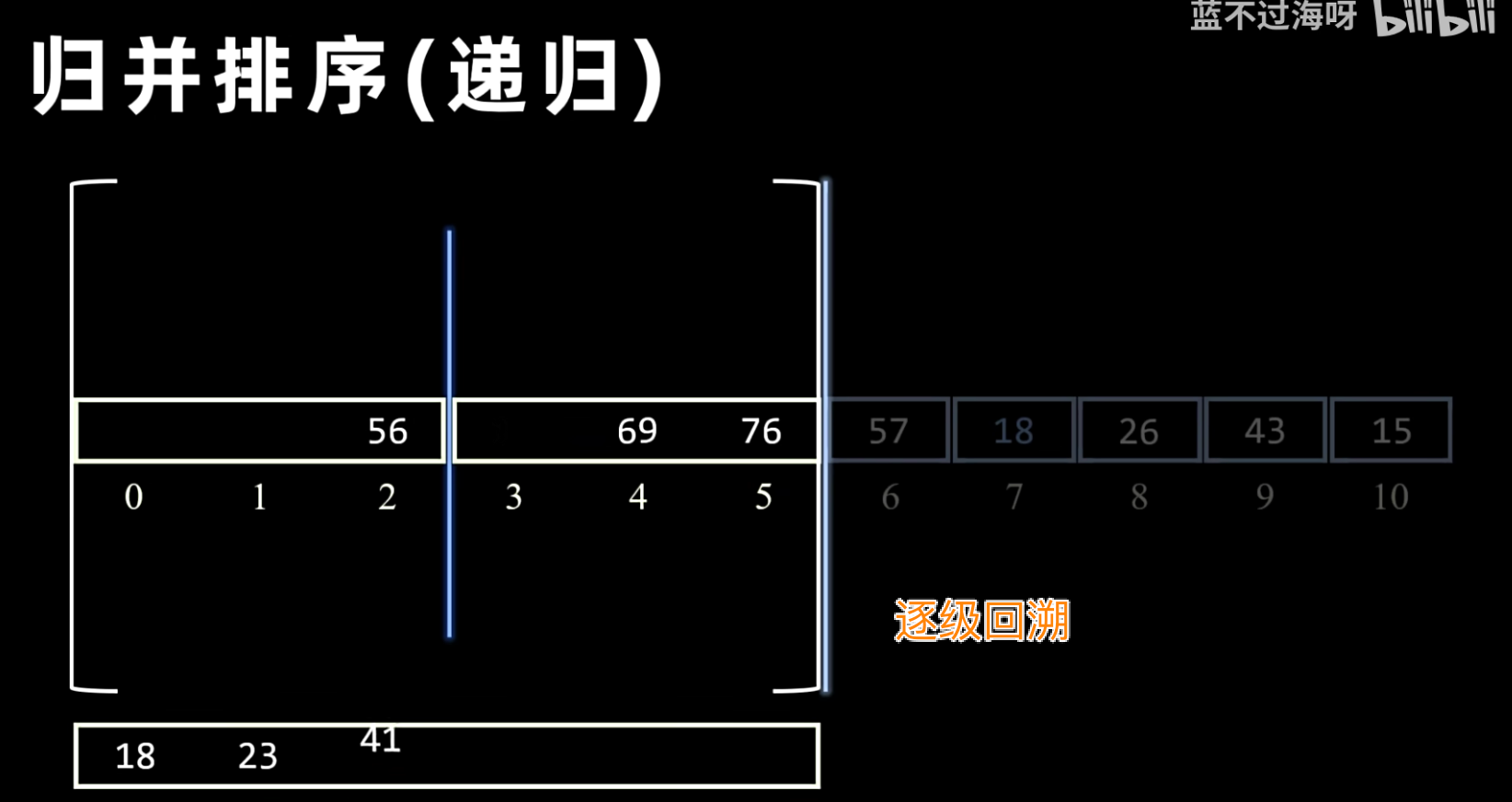
- 合并:将两个已排序的子序列合并成一个大的有序序列。合并操作通过比较两个子序列的元素,将较小(或较大)的元素放入一个新的临时数组中,直到一个子序列为空,然后将另一个子序列剩余的元素全部复制到临时数组末尾。最后,将临时数组的内容复制回原数组。
- 性能分析:
- 时间复杂度:
- 最好、最坏、平均情况:都是 。分解过程产生 层递归,每层递归的合并操作需要 的时间。
- 空间复杂度:,因为合并操作需要一个与原始序列大小相同的临时数组。
- 稳定性:归并排序是稳定的排序算法。在合并过程中,如果两个元素相等,可以规定先放入左边子序列的元素,从而保证相等元素的相对顺序不变。
- 时间复杂度:
- k 路归并
- 归并路数 k (Ways of Merge): 在一次归并操作中,同时合并的归并段数量。例如,二路归并的
k=2,五路归并的k=5。 - 假设有 m 个初始归并段,进行 k 路归并,则完成整个排序所需的归并趟数
s为:
- 归并路数 k (Ways of Merge): 在一次归并操作中,同时合并的归并段数量。例如,二路归并的



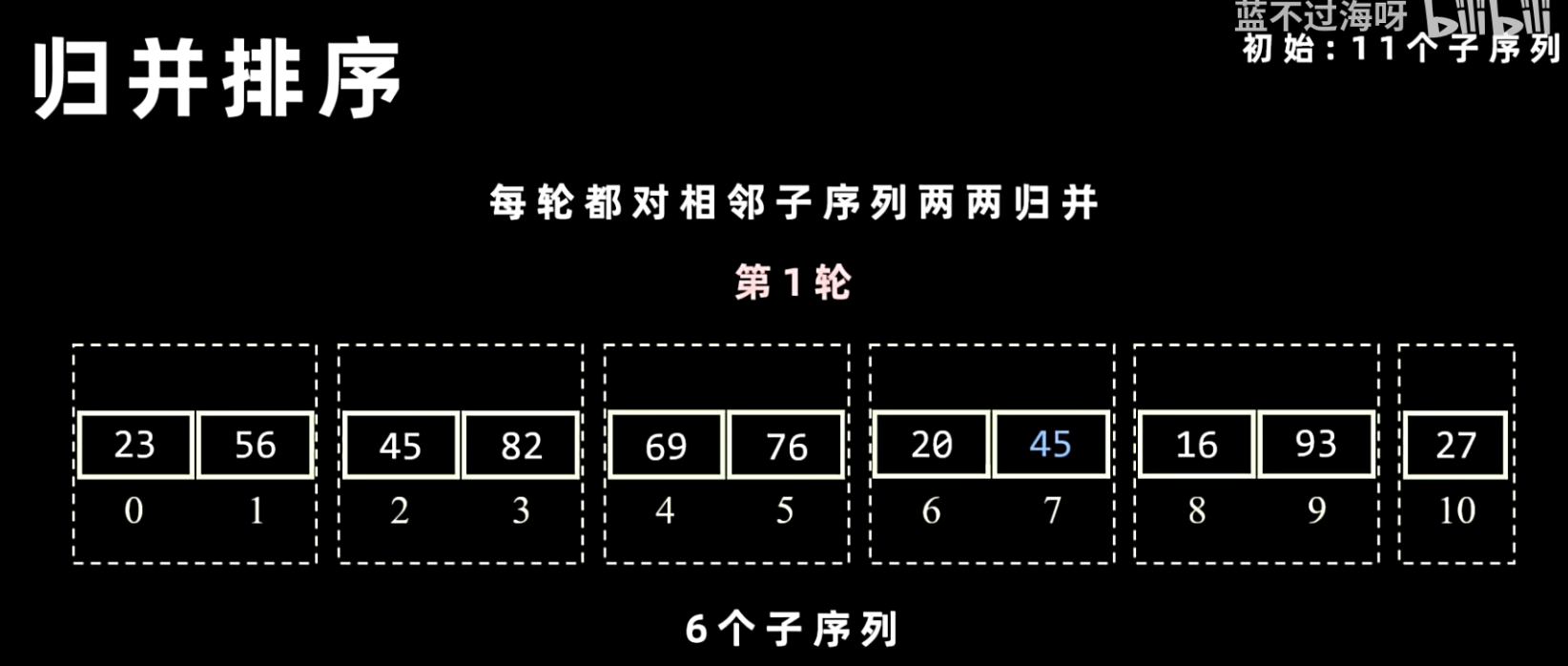



![[attachment/00317b39adae08ca30c48b1b2c3eb8ad_MD5.png|归并排序是稳定的]]
递归方法
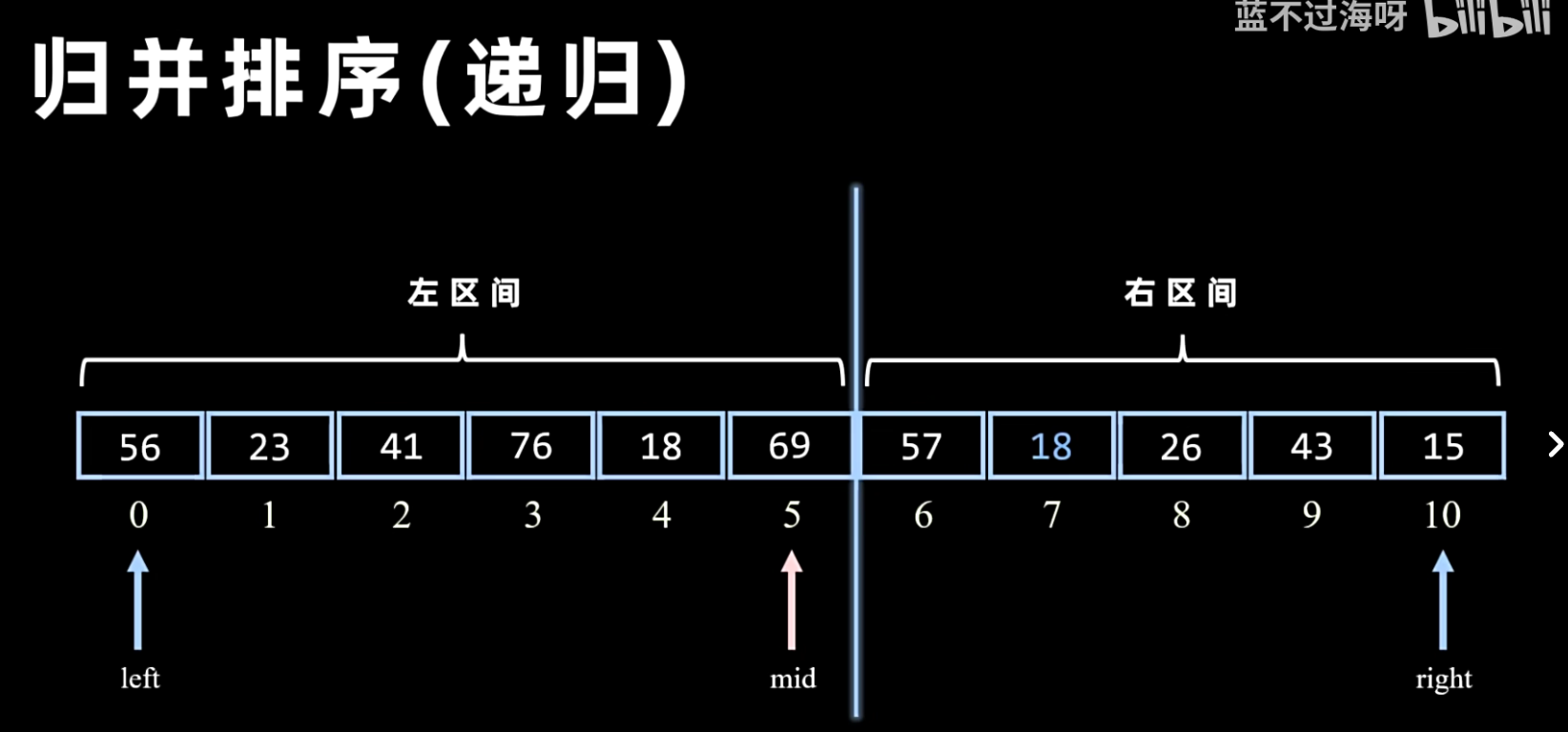
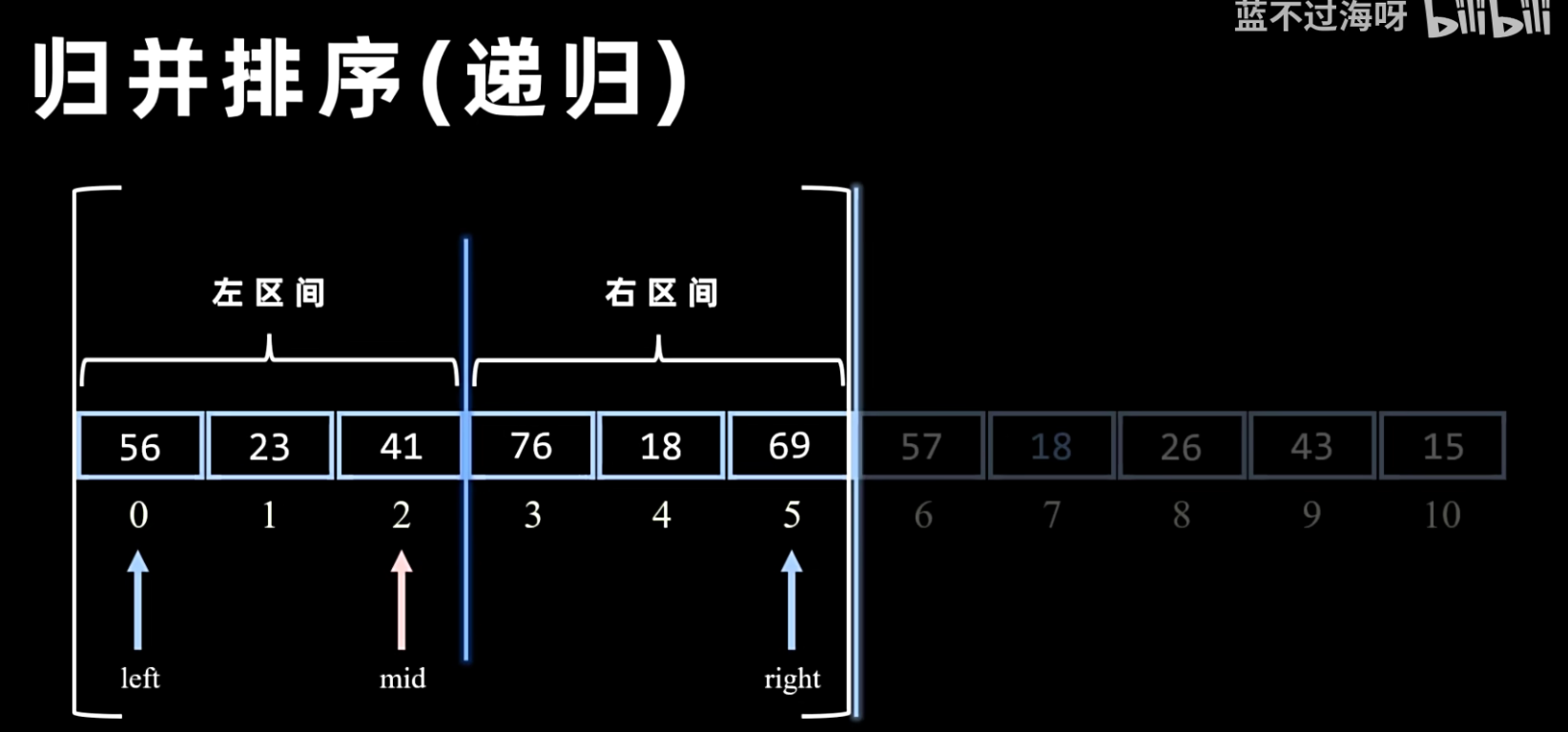
基数排序
- 算法思想:
- 基数排序(Radix Sort)是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
- 适用于待排序数据可以表示为多个“位”的形式,且每一位上的取值范围不大。
- 算法过程:
- 确定最大位数:找出待排序序列中最大元素的位数,决定需要进行多少轮排序。
- 分配与收集:
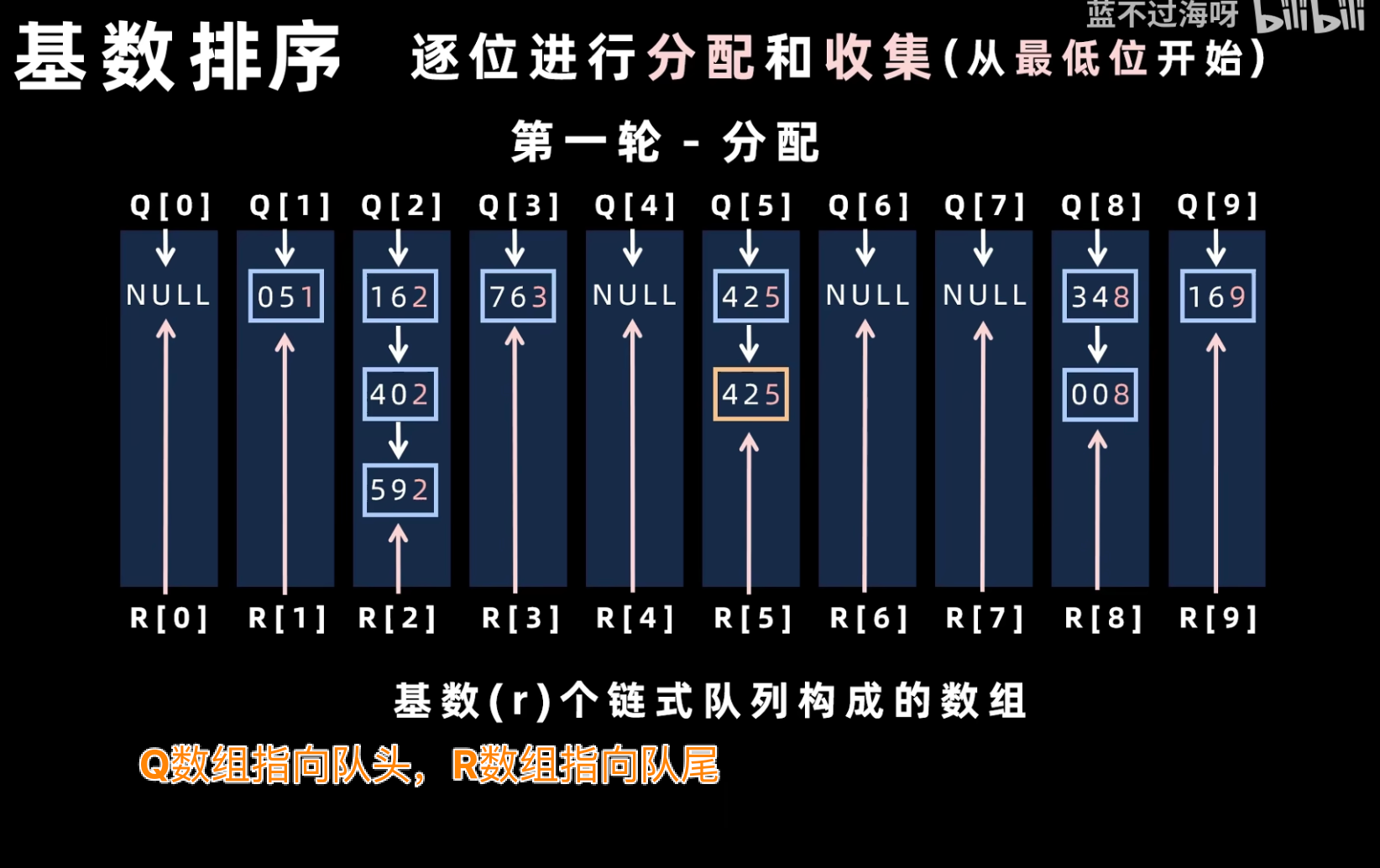
- 分配(Distribute):从最低位(个位)开始,按照当前位的值将元素分配到 0-9 的 10 个桶中。
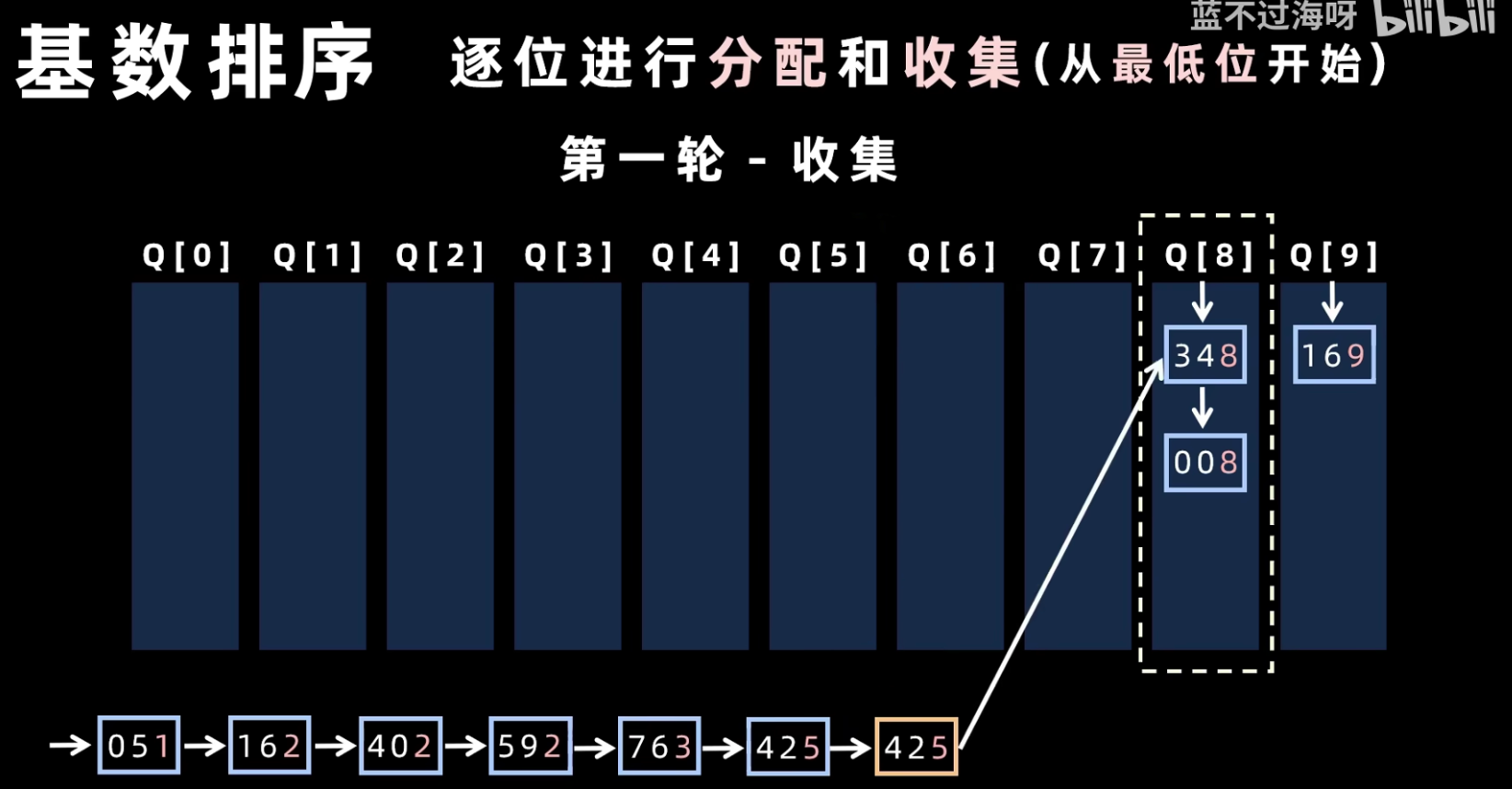
- 收集(Gather):将所有桶中的元素按顺序收集起来,形成新的序列。
- 重复上述分配和收集过程,直到最高位。
- 性能分析:
- 时间复杂度:
- 设 是元素个数, 是最大元素的位数, 是基数(通常取 10)。
- 时间复杂度为 。在桶排序中,每次分配和收集需要 的时间。
- 如果 和 较小,则效率很高。
- 空间复杂度:,需要额外的空间来存储桶(链表),如果是数组则需要 。
- 稳定性:基数排序是稳定的排序算法。在每次分配和收集时,只要保证相同位值的元素在桶中和收集时保持原有顺序,就能保证稳定性。
- 时间复杂度:
- 适用性:
- 适用于非负整数排序。
- 对位数较少、数值范围不大的整数排序效率高。



![[attachment/d3a7b5ca7aec7247b03d8a90aafbcc4b_MD5.png|在第一轮的基础上进行第二轮比较]]




计数排序
- 算法思想:
- 计数排序(Counting Sort)是一种非比较型整数排序算法,其核心思想是利用一个额外的数组来存储输入数组中每个元素的出现次数。
- 适用于待排序数据是整数,且范围不大的情况。
- 实际上是一种一一映射的哈希,统计每个关键字出现的次数
- 算法过程:
- 确定范围:找出待排序序列中最大值和最小值,确定数据的范围 。
- 计数:创建一个计数数组
count,大小为max - min + 1。遍历输入序列,将每个元素出现的次数记录在count数组的对应位置。例如,元素x出现的次数记录在count[x - min]。 - 累加:修改
count数组,使其每个位置存储的是小于或等于其索引的元素的总个数。即count[i] = count[i] + count[i-1]。 - 输出:从输入序列的末尾开始遍历(为了保证稳定性),将每个元素
x放到输出数组的count[x - min] - 1位置,然后将count[x - min]减 1。
- 性能分析:
- 时间复杂度:
- 设 是元素个数, 是数据范围(
max - min + 1)。 - 时间复杂度为 。
- 设 是元素个数, 是数据范围(
- 空间复杂度:,用于存储计数数组。
- 稳定性:计数排序是稳定的排序算法。通过从后向前遍历输入序列进行输出,可以保证相等元素的相对顺序不变。
- 时间复杂度:
- 适用性:
- 适用于整数排序。
- 当数据范围 远小于元素个数 的平方时,效率很高。
- 当数据范围 很大时,不适用,因为会消耗大量的空间。