二次型

定义

$n$ 个变量 $x_1,x_2,\dots ,x_n$ 的二次型 (Quadratic Form) 是一个关于这些变量的齐次二次多项式，其一般形式为：

$f(x_1,x_2,\dots ,x_n)={\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}{x}_i{x}_j$

其中 $a_{ij}$ 为常数。

例如，三元二次型的一般形式为：

$f(x_1,x_2,x_3)=a_{11}{x}_1^2+a_{22}{x}_2^2+a_{33}{x}_3^2+2a_{12}{x}_1{x}_2+2a_{13}{x}_1{x}_3+2a_{23}{x}_2{x}_3$

注意，这里将交叉项 $x_i{x}_j$ ($i\ne j$) 的系数写为 $2a_{ij}$ 是为了方便后续的矩阵表示。

矩阵表示

任何一个二次型 $f(x_1,x_2,\dots ,x_n)$ 都可以唯一地表示为矩阵乘积的形式。

令列向量 $\mathbf{x}=\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)$，则二次型可以写成：

$f(\mathbf{x})={\mathbf{x}}^{T}A\mathbf{x}$

其中，$A$ 是一个 $n\times n$ 的对称矩阵 (Symmetric Matrix)，称为二次型的矩阵。矩阵 $A$ 的元素构造如下：

• 对角线元素 $a_{ii}$ 是 $x_i^2$ 项的系数。
• 非对角线元素 $a_{ij}=a_{ji}$ ($i\ne j$) 是 $x_i{x}_j$ 项系数的一半。

示例： 对于二次型 $f(x_1,x_2,x_3)=x_1^2-2x_2^2+4x_3^2+2x_1{x}_2-6x_1{x}_3+4x_2{x}_3$，其矩阵表示为： $A=\left(\begin{array}{ccc}1& 1& -3\\ 1& -2& 2\\ -3& 2& 4\end{array}\right),\mathbf{x}=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)$ 于是 $f(x_1,x_2,x_3)={\mathbf{x}}^{T}A\mathbf{x}$。

二次型的秩 (Rank) 定义为其对应矩阵 $A$ 的秩，记作 $r(f)$ 或 $r(A)$。

标准形与规范形

通过变量的可逆线性变换 $\mathbf{x}=C\mathbf{y}$，可以将二次型化为更简单的形式。

标准形

二次型的标准形是指只含有平方项的二次型，其一般形式为：

$f=d_1{y}_1^2+d_2{y}_2^2+\cdots +d_n{y}_n^2$

其中 $d_i$ 是系数。任何二次型都可以通过合适的线性变换化为标准形。

• 配方法：通过配方将原二次型化为平方和的形式，从而得到标准形和相应的线性变换。
• 正交变换法：对于二次型 $f={\mathbf{x}}^{T}A\mathbf{x}$，必存在正交矩阵 (Orthogonal Matrix) $P$，使得 $\mathbf{x}=P\mathbf{y}$，将二次型化为标准形： $f={\mathbf{y}}^T(P^{T}AP)\mathbf{y}={\mathbf{y}}^T\Lambda \mathbf{y}={\lambda }_1{y}_1^2+{\lambda }_2{y}_2^2+\cdots +{\lambda }_n{y}_n^2$ 其中 $\Lambda$ 是以矩阵 $A$ 的特征值 (Eigenvalues) ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ 为对角元素的对角矩阵。

规范形

规范形是在标准形的基础上进一步简化的形式，其平方项的系数只为 $1,-1$ 或 $0$。 $f=z_1^2+\cdots +z_p^2-z_{p+1}^2-\cdots -z_r^2$ 其中 $r$ 是二次型的秩。

惯性定理

对于一个实二次型，不论选取什么样的可逆线性变换将其化为标准形或规范形，其标准形中正系数的个数$p$ 和负系数的个数$q$ 都是唯一确定的。

• $p$ 被称为正惯性指数 (Positive Index of Inertia)。
• $q$ 被称为负惯性指数 (Negative Index of Inertia)。
• 二次型的秩 $r=p+q$。
• $(p,q)$ 称为二次型的符号差 (Signature)。

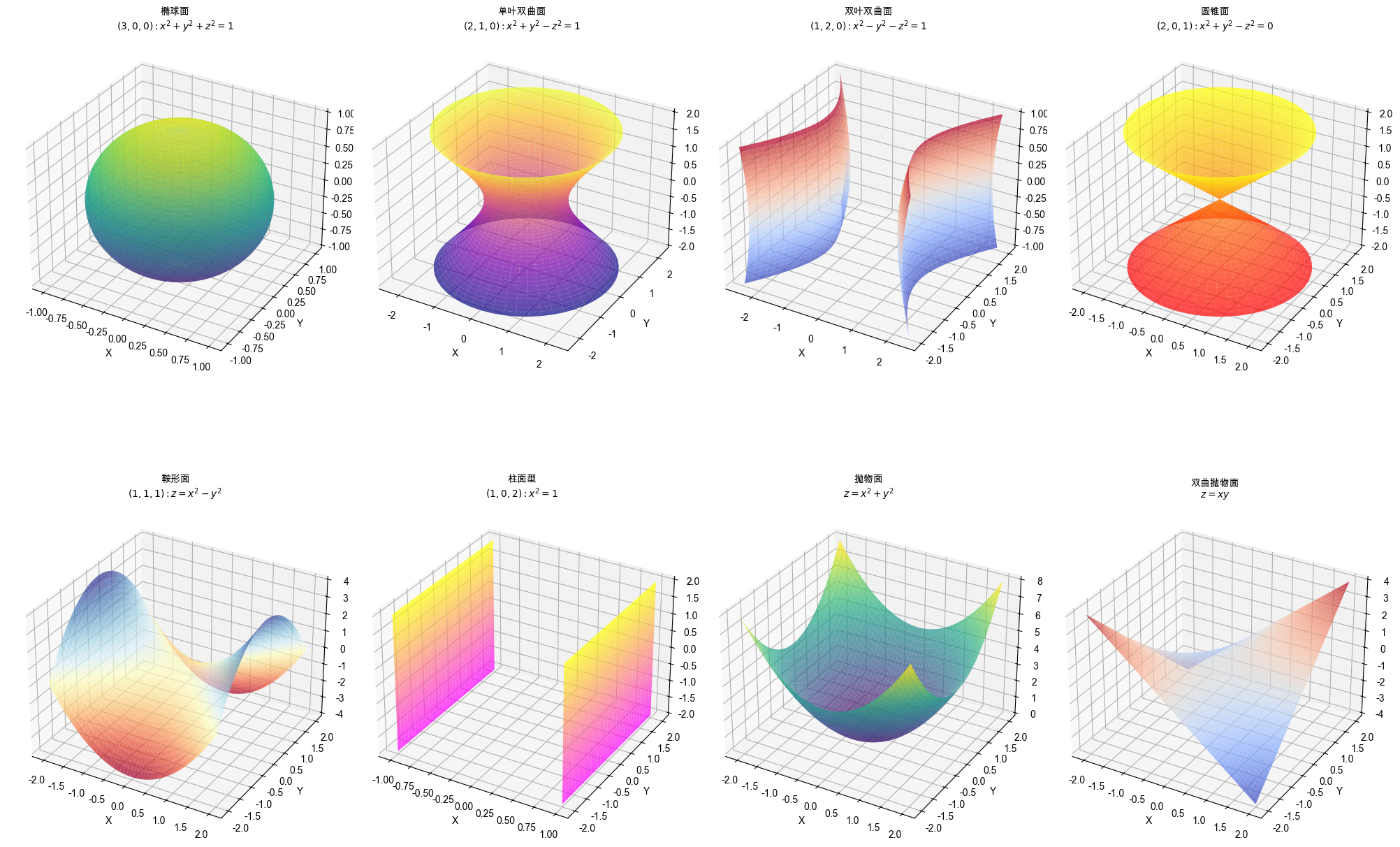
几类典型图像

惯性系数 $(p,q,r)$	二次型标准形式	几何形状类型（典型图像）	示例
$(n,0,0)$	$x_1^2+\cdots +x_n^2$	椭球面、球面、实轴正定型	$x^2+y^2+z^2=1$
$(n-1,1,0)$	$x_1^2+\cdots +x_{n-1}^2-x_n^2$	单叶双曲面（Hyperboloid of One Sheet）	$x^2+y^2-z^2=1$
$(1,n-1,0)$	$x_1^2-x_2^2-\cdots -x_n^2$	双叶双曲面（Hyperboloid of Two Sheets）	$x^2-y^2-z^2=1$
$(n-1,0,1)$	$x_1^2+\cdots +x_{n-1}^2$	圆锥面（Cone）	$x^2+y^2-z^2=0$
$(1,1,1)$	$x^2-y^2$	鞍形面（Saddle, 退化双曲面）	$x^2-y^2=0$
$(1,0,n-1)$	$x_1^2$	折线、抛物槽、柱面型	$x^2=0$，其他变量为自由方向
$(0,0,n)$	$0$	零平面	全零二次型