常用三角函数

请总结三角函数定义，及相关和差角公式、和积化差公式、倍角公式、半角公式、正弦定理、余弦定理和反三角函数性质

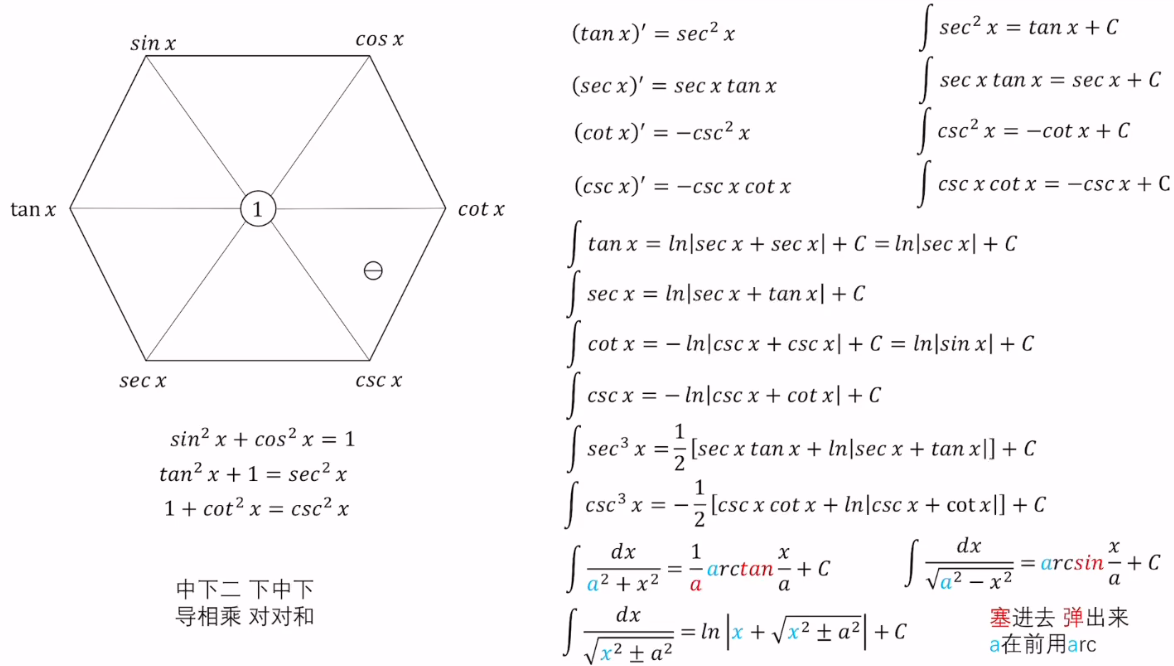
三角函数定义

直角三角形定义

在直角三角形中，设 $\alpha$ 为锐角：

• $\sin \alpha =\frac{\text{对边}}{\text{斜边}}$
• $\cos \alpha =\frac{\text{邻边}}{\text{斜边}}$
• $\tan \alpha =\frac{\text{对边}}{\text{邻边}}$
• $\cot \alpha =\frac{\text{邻边}}{\text{对边}}$
• $\sec \alpha =\frac{\text{斜边}}{\text{邻边}}$ secant
• $\csc \alpha =\frac{\text{斜边}}{\text{对边}}$ cosecant

常用相互转换

三角函数常用的相互转换公式

常用三角函数

定义

1. 正弦函数：$\sin \theta =\frac{\text{对边}}{\text{斜边}}$
2. 余弦函数：$\cos \theta =\frac{\text{邻边}}{\text{斜边}}$
3. 正切函数：$\tan \theta =\frac{\sin \theta }{\cos \theta }=\frac{\text{对边}}{\text{邻边}}$
4. 余切函数：$\cot \theta =\frac{1}{\tan \theta }$
5. 正割函数：$\sec \theta =\frac{1}{\cos \theta }$
6. 余割函数：$\csc \theta =\frac{1}{\sin \theta }$

基本性质

1. 周期性：
   • $\sin (\theta +2\pi )=\sin \theta$
   • $\cos (\theta +2\pi )=\cos \theta$
   • $\tan (\theta +\pi )=\tan \theta$
2. 奇偶性：
   • $\sin (-\theta )=-\sin \theta$（奇函数）
   • $\cos (-\theta )=\cos \theta$（偶函数）
   • $\tan (-\theta )=-\tan \theta$（奇函数）

常用相互转换公式

1. 倒数关系

$$\sec \theta =\frac{1}{\cos \theta },\csc \theta =\frac{1}{\sin \theta },\cot \theta =\frac{1}{\tan \theta }$$

2. 平方和关系

$${\sin }^2\theta +{\cos }^2\theta =1\text{（证明：利用单位圆上点的坐标平方和为1）}$$ $$1+{\tan }^2\theta ={\sec }^2\theta \text{（两边同乘 cos2θ 可推出）}$$

3. 相位转换

$$\sin \left(\theta +\frac{\pi }{2}\right)=\cos \theta ,\cos \left(\theta -\frac{\pi }{2}\right)=\sin \theta$$ $$\sin (\pi -\theta )=\sin \theta ,\cos (\pi -\theta )=-\cos \theta$$

4. 和角公式

$$\sin (\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$$ $$\cos (\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$$

5. 倍角与半角公式

倍角公式：

$$\sin 2\theta =2\sin \theta \cos \theta ,\cos 2\theta ={\cos }^2\theta -{\sin }^2\theta$$

半角公式：

$$\sin \frac{\theta }{2}=\pm \sqrt{\frac{1-\cos \theta }{2}},\cos \frac{\theta }{2}=\pm \sqrt{\frac{1+\cos \theta }{2}}$$

单位圆定义

设点 $P(x,y)$ 在单位圆上对应角 $\theta$：

• $\sin \theta =y$
• $\cos \theta =x$
• $\tan \theta =\frac{y}{x}$ （$x\ne 0$）

---

和差角公式

$$\begin{array}{rl}\sin (\alpha \pm \beta )& =\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos (\alpha \pm \beta )& =\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ \tan (\alpha \pm \beta )& =\frac{\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }\end{array}$$

证明： 以 $\cos (\alpha -\beta )$ 为例，设单位圆上两点 $A(\cos \alpha ,\sin \alpha )$，$B(\cos \beta ,\sin \beta )$，利用向量点积：

$$\cos (\alpha -\beta )=\overrightarrow{OA}\cdot \overrightarrow{OB}=\cos \alpha \cos \beta +\sin \alpha \sin \beta$$

---

和积互化公式

和化积

$$\begin{array}{rl}\sin \alpha +\sin \beta & =2\sin \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)\\ \sin \alpha -\sin \beta & =2\cos \left(\frac{\alpha +\beta }{2}\right)\sin \left(\frac{\alpha -\beta }{2}\right)\\ \cos \alpha +\cos \beta & =2\cos \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)\\ \cos \alpha -\cos \beta & =-2\sin \left(\frac{\alpha +\beta }{2}\right)\sin \left(\frac{\alpha -\beta }{2}\right)\end{array}$$

积化和

$$\begin{array}{rl}\sin \alpha \cos \beta & =\frac{1}{2}[\sin (\alpha +\beta )+\sin (\alpha -\beta )]\\ \cos \alpha \sin \beta & =\frac{1}{2}[\sin (\alpha +\beta )-\sin (\alpha -\beta )]\\ \cos \alpha \cos \beta & =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )]\\ \sin \alpha \sin \beta & =-\frac{1}{2}[\cos (\alpha +\beta )-\cos (\alpha -\beta )]\end{array}$$

应用场景：信号处理中的频谱分析、三角积分化简。

---

倍角公式

$$\begin{array}{rl}\sin 2\alpha & =2\sin \alpha \cos \alpha \\ \cos 2\alpha & ={\cos }^2\alpha -{\sin }^2\alpha =2{\cos }^2\alpha -1=1-2{\sin }^2\alpha \\ \tan 2\alpha & =\frac{2\tan \alpha }{1-{\tan }^2\alpha }\\ \sin 3\alpha & =3\sin \alpha -4{\sin }^3\alpha \\ \cos 3\alpha & =4{\cos }^3\alpha -3\cos \alpha \end{array}$$

推导：令 $\beta =\alpha$ 代入和角公式。

---

半角公式

$$\begin{array}{rl}\sin \frac{\alpha }{2}& =\pm \sqrt{\frac{1-\cos \alpha }{2}}\\ \cos \frac{\alpha }{2}& =\pm \sqrt{\frac{1+\cos \alpha }{2}}\\ \tan \frac{\alpha }{2}& =\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}=\frac{\sin \alpha }{1+\cos \alpha }\end{array}$$

注：符号由 $\frac{\alpha }{2}$ 所在象限决定。

---

正弦定理

在任意三角形中：

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$

其中 $R$ 为外接圆半径。

应用场景：已知两角一边求其他边。

---

余弦定理

在任意三角形中：

$$a^2=b^2+c^2-2bc\cos A$$

应用场景：已知三边求角或已知两边夹角求第三边。

---

反三角函数性质

定义域与值域

函数	定义域	值域
$\arcsin x$	$[-1,1]$	$[-\frac{\pi }{2},\frac{\pi }{2}]$
$\arccos x$	$[-1,1]$	$[0,\pi ]$
$\arctan x$	$\mathbb{R}$	$(-\frac{\pi }{2},\frac{\pi }{2})$

导数公式

$$\begin{array}{rl}\frac{d}{dx}\arcsin x& =\frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\arccos x& =-\frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\arctan x& =\frac{1}{1+x^2}\end{array}$$

恒等式

$$\arcsin x+\arccos x=\frac{\pi }{2}$$

双曲函数

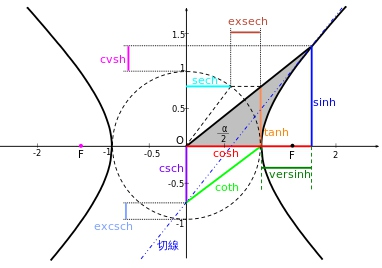
双曲余弦函数 (Hyperbolic Cosine)

定义:

$$\cosh x=\frac{e^x+e^{-x}}{2}$$

性质:

• 偶函数: $\cosh (-x)=\cosh x$
• 导数关系: $\frac{d}{dx}\cosh x=\sinh x$
• 泰勒展开: $\cosh x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots$

双曲正弦函数 (Hyperbolic Sine)

定义:

$$\sinh x=\frac{e^x-e^{-x}}{2}$$

性质:

• 奇函数: $\sinh (-x)=-\sinh x$
• 导数关系: $\frac{d}{dx}\sinh x=\cosh x$
• 泰勒展开: $\sinh x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots$

双曲正切函数 (Hyperbolic Tangent)

定义:

$$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

性质:

• 奇函数: $\tanh (-x)=-\tanh x$
• 导数关系: $\frac{d}{dx}\tanh x={\text{sech}}^{2}x=1-{\tanh }^{2}x$
• 渐近行为: ${\lim }_{x\to \infty }\tanh x=1$, ${\lim }_{x\to -\infty }\tanh x=-1$

基本恒等式

$${\cosh }^{2}x-{\sinh }^{2}x=1$$ $$1-{\tanh }^{2}x={\text{sech}}^{2}x$$

应用场景

1. 悬链线问题 (Catenary): 描述悬挂在两点的链条形状
2. 狭义相对论: 洛伦兹变换中的双曲函数表示
3. 积分计算: 某些积分通过双曲函数代换简化
4. 微分方程: 双曲函数是某些微分方程的解

与三角函数的类比

双曲函数与三角函数有相似但不完全相同的性质:

• 双曲函数用指数函数定义，三角函数用单位圆定义
• 双曲函数的参数可以解释为双曲线下的面积