弧长公式

核心思想：万变不离其宗的弧长微元

所有弧长公式都源于同一个几何思想：将一小段曲线弧长 $ds$ 近似为一条直线段，其长度由勾股定理确定。

在二维直角坐标系中，这个基本关系是：

$$d{s}^2=d{x}^2+d{y}^2$$ $$ds=\sqrt{d{x}^2+d{y}^2}$$

我们所有的弧长公式，都只是将这个基本微元 $ds$ 用不同坐标系的变量（如 $x,t,\theta$）来表达，然后进行积分。

1. 直角坐标 (Cartesian Coordinates)

形式一：$y=f(x)$

• 适用场景：曲线可以表示为 $y$ 关于 $x$ 的显函数。
• 推导：从 $ds=\sqrt{d{x}^2+d{y}^2}$ 出发，提出 $dx$。

$$ds=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx$$

• 积分公式：

$$L={\int }_a^b\sqrt{1+[f^{\prime }(x){]}^2}dx$$

形式二：$x=g(y)$

• 适用场景：曲线可以表示为 $x$ 关于 $y$ 的显函数（例如，垂直的抛物线）。
• 推导：从 $ds=\sqrt{d{x}^2+d{y}^2}$ 出发，提出 $dy$。

$$ds=\sqrt{{\left(\frac{dx}{dy}\right)}^2+1}dy$$

• 积分公式：

$$L={\int }_c^d\sqrt{1+[g^{\prime }(y){]}^2}dy$$

2. 参数方程 (Parametric Equations)

• 形式：$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$
• 适用场景：最通用的形式，特别适用于无法表示为显函数的曲线（如圆、摆线）或描述质点运动轨迹。
• 推导：将 $dx$ 和 $dy$ 用参数 $t$ 的微分来表示。

$$dx=x^{\prime }(t)dt,dy=y^{\prime }(t)dt$$

代入基本关系：

$$d{s}^2=[x^{\prime }(t)dt{]}^2+[y^{\prime }(t)dt{]}^2=\left([x^{\prime }(t){]}^2+[y^{\prime }(t){]}^2\right)d{t}^2$$ $$ds=\sqrt{[x^{\prime }(t){]}^2+[y^{\prime }(t){]}^2}dt$$

• 积分公式：

$$L={\int }_{t_1}^{t_2}\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}dt$$

• 关键联系：直角坐标是参数方程的特例。例如，对于 $y=f(x)$，可以取参数方程为 $x(t)=t,y(t)=f(t)$，代入上式即可得到直角坐标的公式。

3. 极坐标 (Polar Coordinates)

极坐标下的弧长微元本身有一个更直观的几何形式：$d{s}^2=d{r}^2+(rd\theta {)}^2$。它是由径向变化 $dr$ 和切向变化 $rd\theta$ 构成的微小直角三角形得出的。

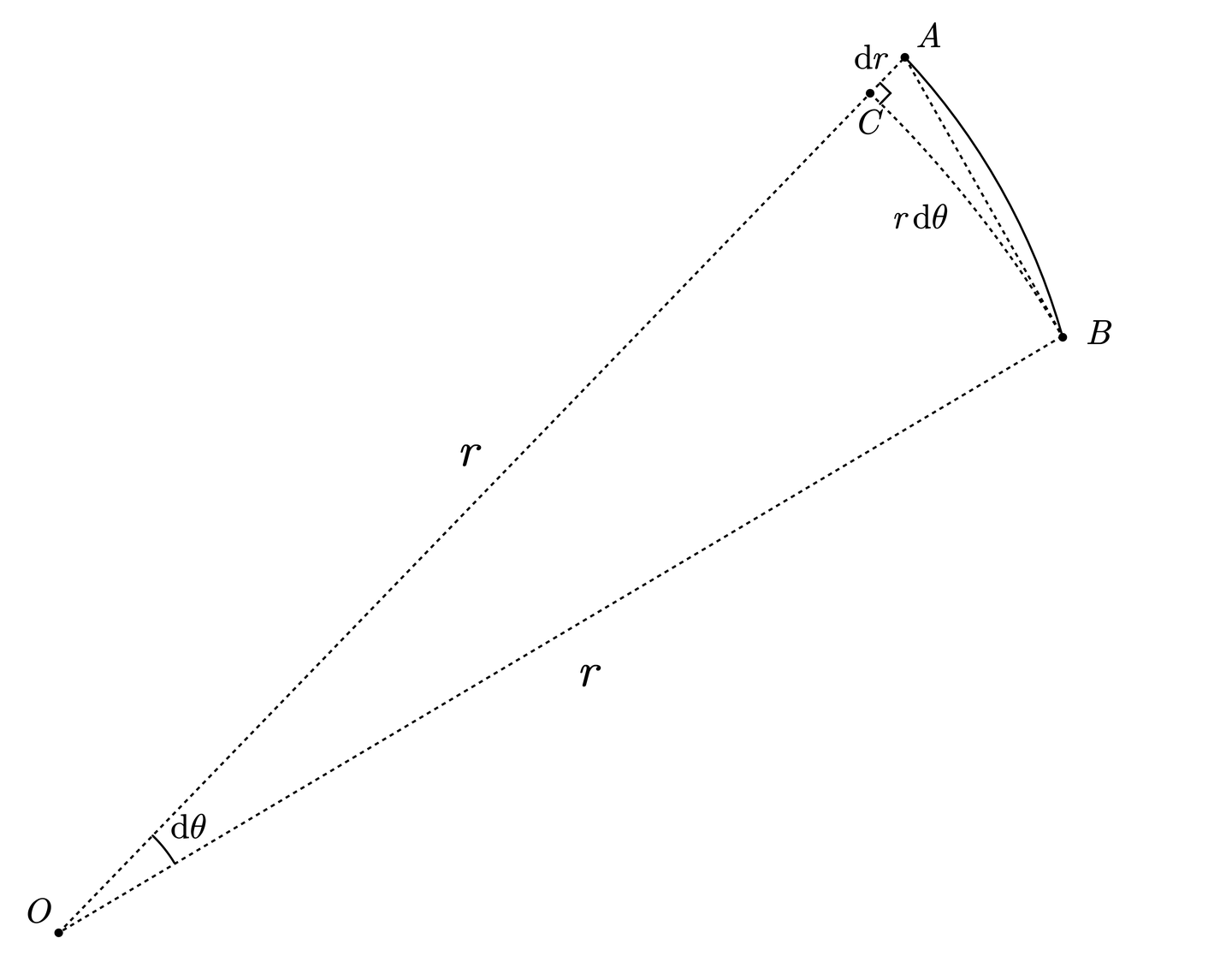
（当然，它也可以通过将 $x=r\cos \theta ,y=r\sin \theta$ 代入参数方程公式进行严格推导，我们上次的讨论就验证了这一点）。

形式一：$r=f(\theta )$

• 适用场景：最常见的极坐标曲线，如心形线、玫瑰线、螺线。
• 推导：从 $d{s}^2=d{r}^2+(rd\theta {)}^2$ 出发，以 $\theta$ 为主变量，提出 $d\theta$。

$$d{s}^2=\left({\left(\frac{dr}{d\theta }\right)}^2+r^2\right)d{\theta }^2$$ $$ds=\sqrt{r^2+{\left(\frac{dr}{d\theta }\right)}^2}d\theta$$

• 积分公式：

$$L={\int }_{\alpha }^{\beta }\sqrt{[f(\theta ){]}^2+[f^{\prime }(\theta ){]}^2}d\theta$$

形式二：$\theta =g(r)$

• 适用场景：不常见，但我们上次的题目就是这个例子。
• 推导：从 $d{s}^2=d{r}^2+(rd\theta {)}^2$ 出发，以 $r$ 为主变量，提出 $dr$。

$$d{s}^2=\left(1+r^2{\left(\frac{d\theta }{dr}\right)}^2\right)d{r}^2$$ $$ds=\sqrt{1+r^2{\left(\frac{d\theta }{dr}\right)}^2}dr$$

• 积分公式：

$$L={\int }_{r_1}^{r_2}\sqrt{1+r^2[g^{\prime }(r){]}^2}dr$$

总结归纳表

坐标系 (System)	函数形式 (Function Form)	弧长微元 ($ds$)	弧长积分公式
直角坐标	$y=f(x)$	$\sqrt{1+(y^{\prime }{)}^2}dx$	$L={\int }_a^b\sqrt{1+[f^{\prime }(x){]}^2}dx$
	$x=g(y)$	$\sqrt{1+(x^{\prime }{)}^2}dy$	$L={\int }_c^d\sqrt{1+[g^{\prime }(y){]}^2}dy$
参数方程	$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$	$\sqrt{(x^{\prime }{)}^2+(y^{\prime }{)}^2}dt$	$L={\int }_{t_1}^{t_2}\sqrt{[x^{\prime }(t){]}^2+[y^{\prime }(t){]}^2}dt$
极坐标	$r=f(\theta )$	$\sqrt{r^2+(r^{\prime }{)}^2}d\theta$	$L={\int }_{\alpha }^{\beta }\sqrt{r^2+(\frac{dr}{d\theta }{)}^2}d\theta$
	$\theta =g(r)$	$\sqrt{1+r^2({\theta }^{\prime }{)}^2}dr$	$L={\int }_{r_1}^{r_2}\sqrt{1+r^2(\frac{d\theta }{dr}{)}^2}dr$