线代运算小专题

形如 AB = kA + lB 的问题

若矩阵 $A,B$ 满足关系式 $AB=kA+lB$，其中 $k,l$ 为非零常数，则该条件暗含了矩阵 $A$ 和 $B$ 之间更深层次的联系。

核心推导： 由 $AB=kA+lB$ 出发，移项得： $AB-kA-lB=O$ 为了构造因子式，在等式两边同时加上 $klE$（$E$ 为单位矩阵）： $AB-kA-lB+klE=klE$ 对左侧进行因式分解，可得： $(A-lE)(B-kE)=klE$ 由于 $k\ne 0$ 且 $l\ne 0$，所以 $klE$ 是一个可逆的对角矩阵。这表明矩阵 $(A-lE)$ 和 $(B-kE)$ 均为可逆矩阵。

结论挖掘：

1. 可逆性: 矩阵 $(A-lE)$ 和 $(B-kE)$ 均可逆。它们的逆矩阵关系为： $(A-lE{)}^{-1}=\frac{1}{kl}(B-kE)$ $(B-kE{)}^{-1}=\frac{1}{kl}(A-lE)$

2. 交换性: 既然 $(A-lE)$ 与 $\frac{1}{kl}(B-kE)$ 互为逆矩阵，它们的位置可以交换，即： $(A-lE)(B-kE)=(B-kE)(A-lE)$ 展开上式两边： $AB-kA-lB+lkE=BA-lA-kB+lkE$ 化简后得到： $AB=BA$ 这表明矩阵 $A$ 和 $B$ 是可交换的。

向量组线性组合的矩阵表示

一个向量组如果可以由另一个向量组线性表示，这种关系可以用矩阵乘法的形式简洁地表达出来。

基本公式： 假设向量组 $({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_s)$ 可由向量组 $({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)$ 线性表示，关系如下： ${\gamma }_j=k_{1j}{\alpha }_1+k_{2j}{\alpha }_2+\cdots +k_{nj}{\alpha }_n,(j=1,2,\dots ,s)$ 这组等式可以写作一个矩阵方程： $[{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_s]=[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n]\left[\begin{array}{cccc}{k}_{11}& k_{12}& \cdots & k_{1s}\\ k_{21}& k_{22}& \cdots & k_{2s}\\ ⋮& ⋮& \ddots & ⋮\\ k_{n1}& k_{n2}& \cdots & k_{ns}\end{array}\right]$ 若记 $C=[{\gamma }_1,\dots ,{\gamma }_s]$，$A=[{\alpha }_1,\dots ,{\alpha }_n]$，$K$ 为系数矩阵，则上式可记为 $C=AK$。

关键记忆点： 新向量组中第 $j$ 个向量 ${\gamma }_j$ 的表示系数，构成了系数矩阵 $K$ 的第 $j$ 列。

示例： $[\begin{array}{ccc}{a}_1\alpha +b_1\beta +c_1\gamma ,& a_2\alpha +b_2\beta +c_2\gamma ,& a_3\alpha +b_3\beta +c_3\gamma \end{array}]=[\begin{array}{ccc}\alpha ,& \beta ,& \gamma \end{array}]\left[\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& c_2& c_3\end{array}\right]$

矩阵乘积与向量组的线性表示

设矩阵 $C=AB$，则矩阵 $C$ 的行、列向量组与矩阵 $A$ 和 $B$ 的向量组之间存在直接的线性表示关系。

核心结论：左乘行，右乘列

• 右乘矩阵 $B$ 决定列向量关系: 乘积矩阵 $C=AB$ 的列向量组可以由 $A$ 的列向量组线性表示，表示的系数矩阵就是 $B$。 $Col(AB)\subseteq Col(A)$ 推导: 设 $A=({\alpha }_1,\dots ,{\alpha }_n)$，$B$ 的第 $j$ 列为 $b_j=(k_{1j},\dots ,k_{nj}{)}^T$。则 $C$ 的第 $j$ 列 $c_j$ 为： $c_j=A{b}_j=k_{1j}{\alpha }_1+k_{2j}{\alpha }_2+\cdots +k_{nj}{\alpha }_n$

• 左乘矩阵 $A$ 决定行向量关系: 乘积矩阵 $C=AB$ 的行向量组可以由 $B$ 的行向量组线性表示，表示的系数矩阵就是 $A$。 $Row(AB)\subseteq Row(B)$ 推导: $C^T=(AB{)}^T=B^T{A}^T$。应用上一条结论到 $C^T$ 上，可知 $C^T$ 的列向量（即 $C$ 的行向量）是 $B^T$ 的列向量（即 $B$ 的行向量）的线性组合。

矩阵乘积的秩

矩阵乘积的秩与原矩阵的秩密切相关。

基本秩不等式

对于任意矩阵 $A_{m\times n}$ 和 $B_{n\times s}$，其乘积的秩满足：

$r(AB)\le \min \{r(A),r(B)\}$

该不等式是 ” 左乘行，右乘列 ” 结论的直接推论。因为 $C$ 的列向量组可由 $A$ 的列向量组表示，所以 $C$ 的列秩不会超过 $A$ 的列秩。同理，$C$ 的行秩不会超过 $B$ 的行秩。

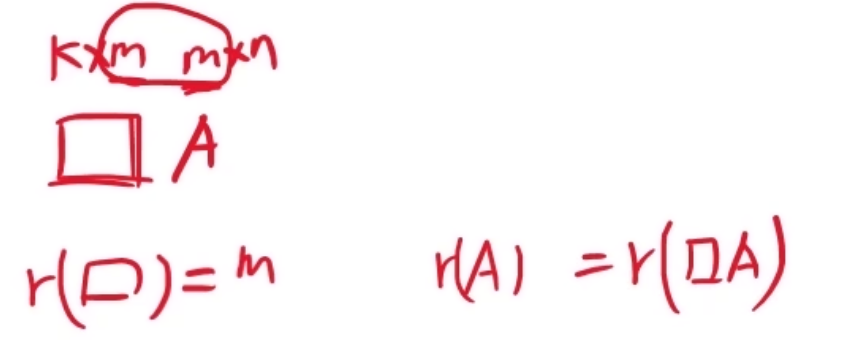
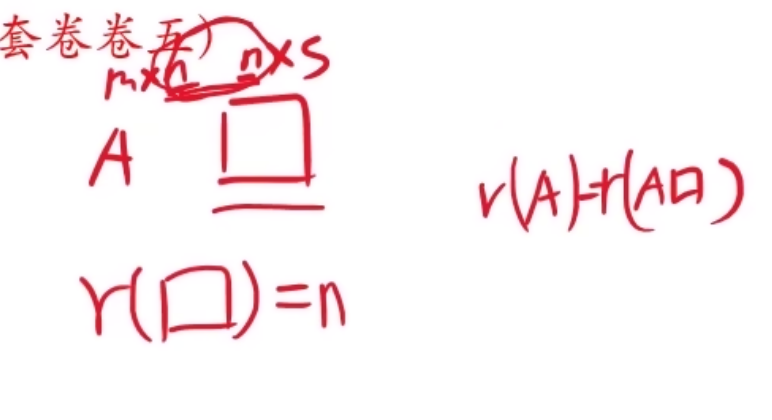
秩的不变性

乘以可逆矩阵，秩不变。 这是一个极为重要的性质，它是矩阵初等变换不改变矩阵秩的理论基础。

• 若 $P$ 是一个 $m\times m$ 的可逆矩阵 (即行、列均满秩的方阵)，$A$ 是一个 $m\times n$ 矩阵，则： $r(PA)=r(A)$
• 若 $Q$ 是一个 $n\times n$ 的可逆矩阵 (即行、列均满秩的方阵)，$A$ 是一个 $m\times n$ 矩阵，则： $r(AQ)=r(A)$

综合结论: 若 $P,Q$ 均为可逆矩阵，则： $r(PAQ)=r(A)$

伴随矩阵与零矩阵的乘积关系

关于 $n$ 阶方阵 $A$ 与其伴随矩阵 $A^{\ast }$，有一组重要的关系，其核心围绕着公式 $A{A}^{\ast }=A^{\ast }A=|A|E$ 展开。

对于任意 $n$ 阶方阵 $A$ ($n\ge 2$)，以下三个条件是等价的：

1. 行列式为零：$|A|=0$
2. 右乘伴随为零：$A{A}^{\ast }=O$
3. 左乘伴随为零：$A^{\ast }A=O$

推导: 这是由基本公式 $A{A}^{\ast }=A^{\ast }A=|A|E$ 直接得出的。当其中任意一个等式成立时（例如 $A^{\ast }A=O$），则必然有 $|A|E=O$。由于单位矩阵 $E$ 不是零矩阵，这必然要求其系数 $|A|=0$。反之，若 $|A|=0$，则 $A{A}^{\ast }=O$ 和 $A^{\ast }A=O$ 显然成立。

伴随矩阵的秩

伴随矩阵 $A^{\ast }$ 的秩 $r(A^{\ast })$ 与原矩阵 $A$ 的秩 $r(A)$ 之间有明确的对应关系： $r(A^{\ast })=\{\begin{array}{ll}n,& \text{当 }r(A)=n\\ 1,& \text{当 }r(A)=n-1\\ 0,& \text{当 }r(A)<n-1\end{array}$

作为齐次方程解的理解

从齐次线性方程组的角度来理解 $A{A}^{\ast }=O$ 和 $A^{\ast }A=O$ 提供了深刻的洞见。

• $A^{\ast }A=O$ 的理解 这个等式意味着，如果将矩阵 $A$ 的每一个列向量代入方程 $A^{\ast }x=0$，等式都成立。因此，矩阵 $A$ 的所有列向量都是齐次线性方程组 $A^{\ast }x=0$ 的解。

• $A{A}^{\ast }=O$ 的理解 同理，这个等式意味着，如果将矩阵 $A^{\ast }$ 的每一个列向量代入方程 $Ax=0$，等式都成立。因此，矩阵 $A^{\ast }$ 的所有列向量都是齐次线性方程组 $Ax=0$ 的解。特别是在 $r(A)=n-1$ 时， $A^{\ast }$ 的非零列向量构成了 $Ax=0$ 的基础解系。