定点数的除法运算
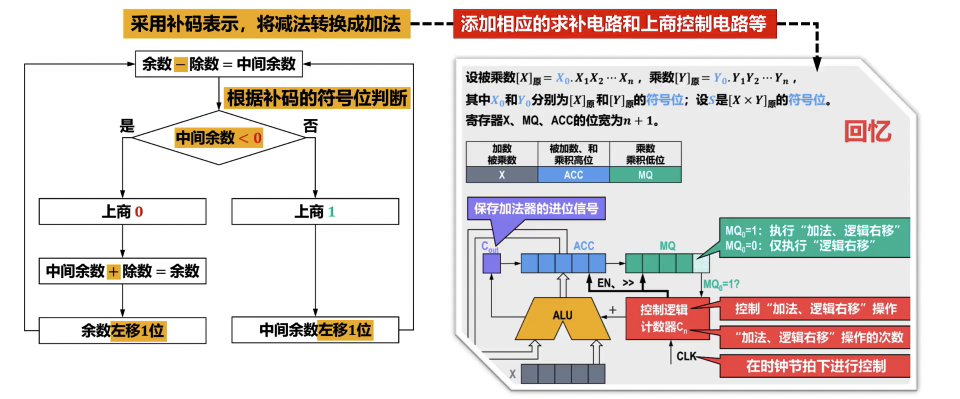
原码除法运算

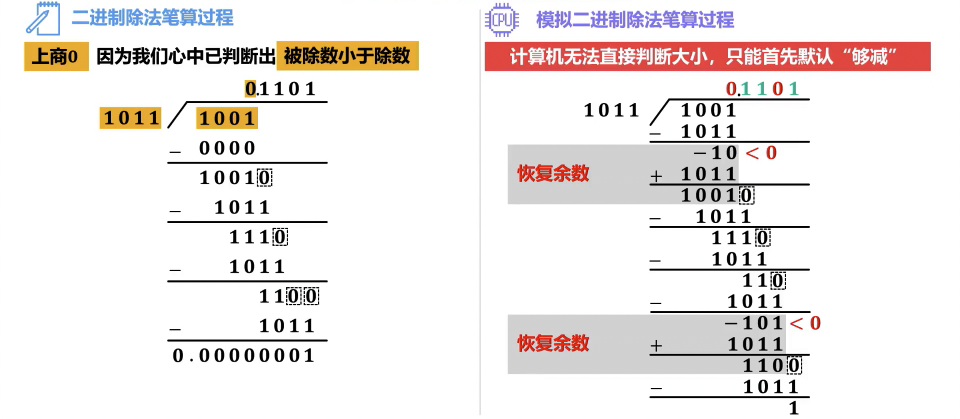
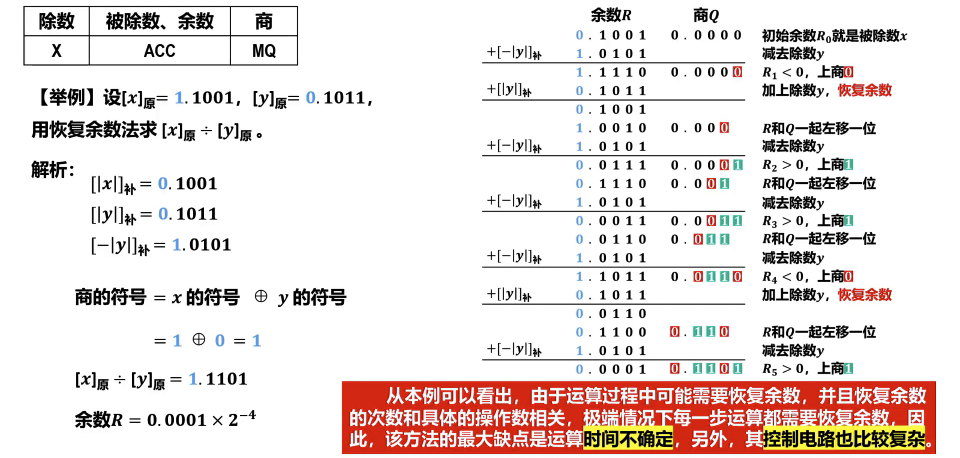
- 恢复余数法:
- 基本思想:每次试商(减去除数),如果余数为负,则表示商位为 0,需要“恢复”余数(加回除数),然后左移;如果余数为正,则商位为 1,直接左移。
- 步骤:部分余数左移一位,减去除数,判断余数符号。若为负,商 0,恢复余数;若为正,商 1。
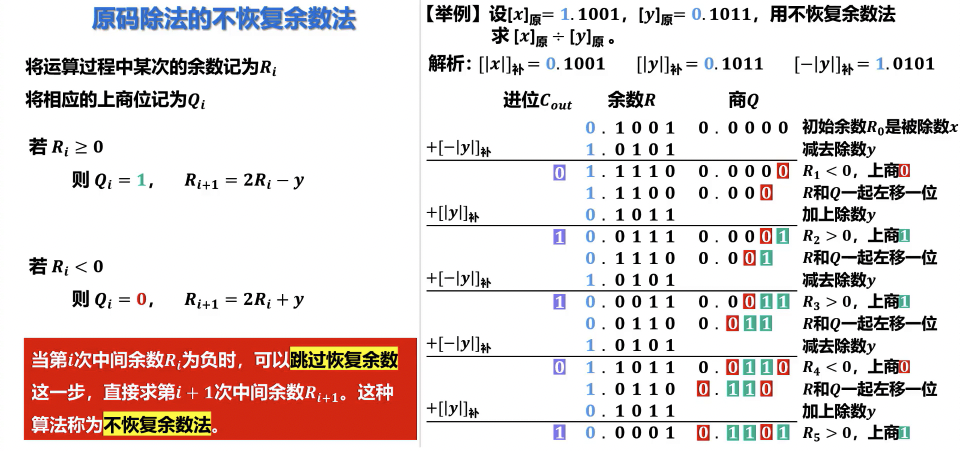
- 不恢复余数法:
- 基本思想:避免了恢复余数的步骤,通过交替加减操作来处理余数。
- 步骤:
- 部分余数和除数符号相同:作减法。
- 部分余数和除数符号不同:作加法。
- 根据操作结果的余数符号确定下一商位(0 或 1)。
- 效率高于恢复余数法。
- 注意:
- 起始操作: 在进行第一次加减操作前,需要将部分余数(或被除数的高位)左移一位。
- 商位确定规则的细化: 在每次操作(加或减)后,根据操作结果(新的部分余数)的符号来确定当前商位:
- 若操作后的新部分余数与除数符号相同,则当前商位为 1。
- 若操作后的新部分余数与除数符号不同,则当前商位为 0。
- 下一次操作的确定: 下一次操作的类型(加或减)取决于当前部分余数的符号(即本次操作后的结果)。
- 若当前部分余数为正,下一步做减法。
- 若当前部分余数为负,下一步做加法。
- (更通用地,应遵循基本思想:若部分余数与除数符号相同,下一步做减法;若不同,下一步做加法。)
- 最终余数校正: 当所有商位确定后,若最终得到的部分余数与被除数符号不同(通常是负数),则需要进行恢复余数操作(即加上除数),以得到正确的最终余数。
- 特殊情况处理: 若运算过程中部分余数为零,则后续商位均为零。
- 与恢复余数法的区别: 不恢复余数法在余数符号不符时,不需要撤销操作(即不用恢复余数),而是直接进行相反操作,从而省去了回退步骤,提高了运算效率。
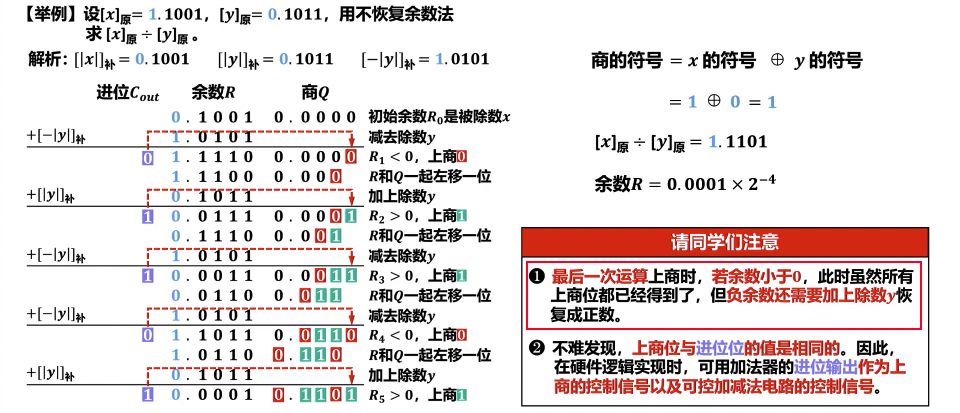
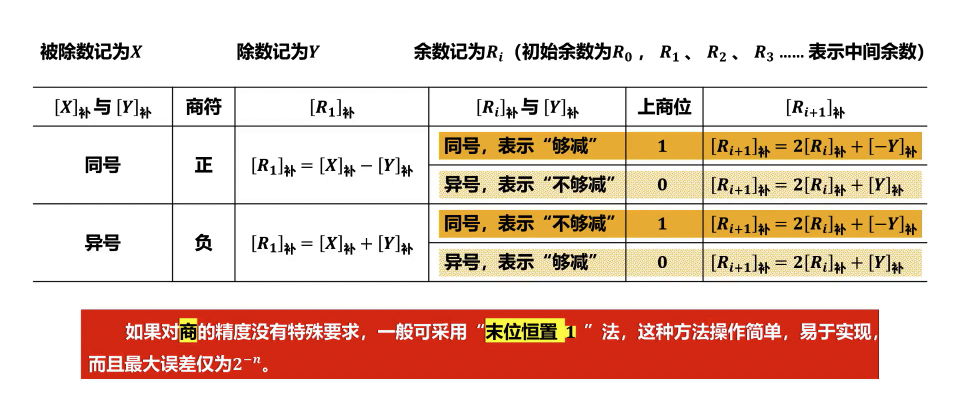
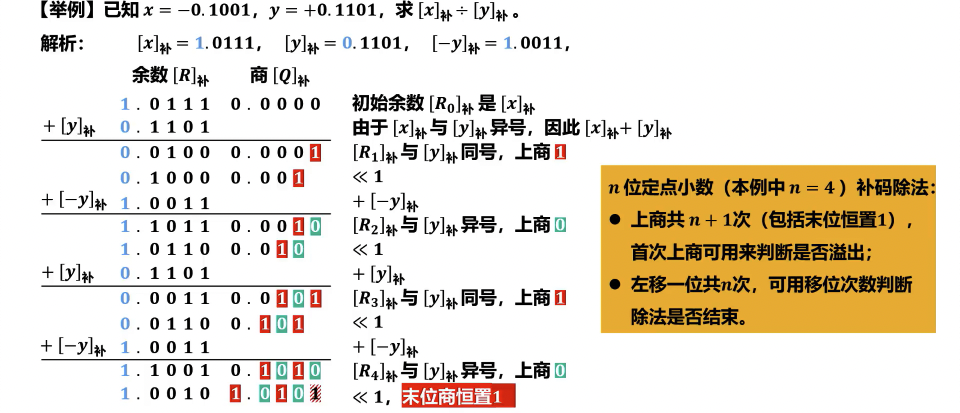
补码除法运算
- 不恢复余数法:
- 初始化:
- 将被除数的数值部分放入商寄存器 Q,部分余数寄存器 A 通常初始化为 0 或与被除数符号位相同。
- 确定除数 D 的补码形式以及其负数的补码形式(即 [-D] 补)。
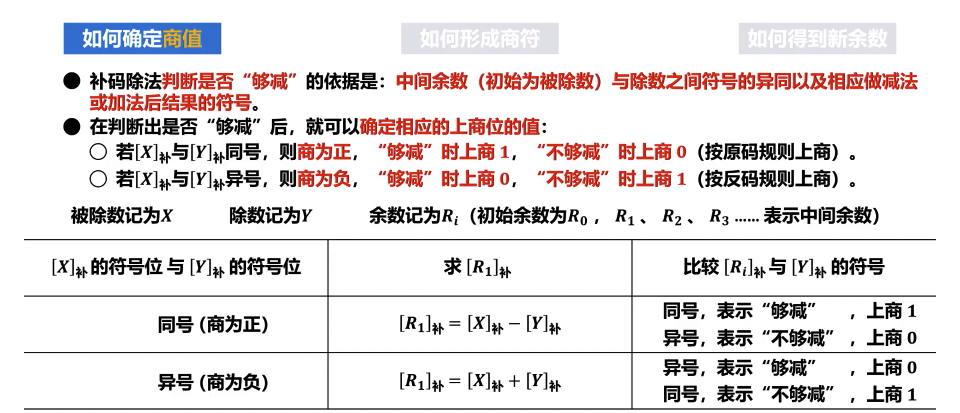
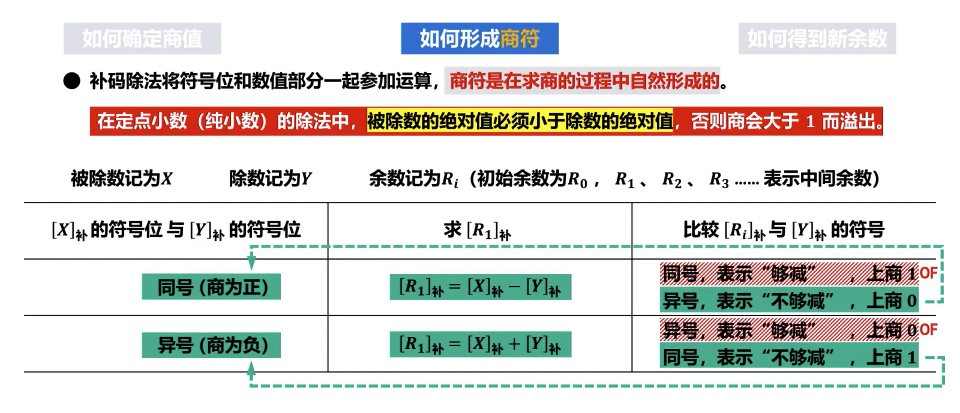
- 商的符号预判:根据被除数和除数的符号(异或结果)确定最终商的符号。若两者符号相同,商为正;若不同,商为负。
- 迭代运算(通常进行 n+1 次,n 为数值位数):
- 左移: 将部分余数寄存器 A 和商寄存器 Q 的内容整体左移一位。A 的符号位不变,Q 的最低位移出,A 的最低位进入 Q 的最高位。
- 判断操作:
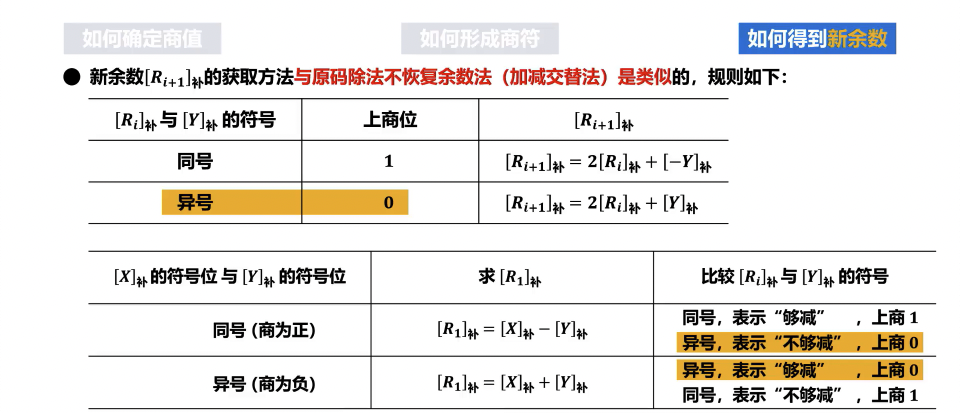
- 若部分余数 A的符号与除数 D的符号相同,执行
A = A + (-D)补(即 A 减去 D)。 - 若部分余数 A的符号与除数 D的符号不同,执行
A = A + D(即 A 加上 D)。
- 若部分余数 A的符号与除数 D的符号相同,执行
- 确定商位:
- 若操作后的新部分余数 A的符号与除数 D的符号相同,则当前商位为 1。
- 若操作后的新部分余数 A的符号与除数 D的符号不同,则当前商位为 0。
- 将确定的商位填入 Q 寄存器的最低位。
- 最终余数校正:
- 当所有商位确定后,A 寄存器中存放的是最终的部分余数。
- 若最终余数 A 的符号与被除数 X 的符号不同(例如,被除数为正但最终余数为负,或被除数为负但最终余数为正):
- 执行恢复操作:若 A 为负,则
A = A + D(加上除数 D);若 A 为正,则A = A + (-D)补(减去除数 D)。 - 校正后的余数 R 应满足:R 的符号与被除数 X 的符号相同,且 |R| < |D|。
- 执行恢复操作:若 A 为负,则
- 最终商的形成:
- Q 寄存器中存储的是商的数值部分。
- 结合第一步预判的商的符号,得到最终的商。若商为负,通常需要将 Q 寄存器中的数值取补码形式。
- 初始化: