224 定点数的乘法运算

定点数的乘法运算

无符号数乘法运算原理

• 移位和相加法：模拟笔算，通过不断移位（逻辑移位）和条件加法（或累加）实现乘积的累加。
• 无符号乘法器：通过组合逻辑电路（如与门和全加器阵列）实现并行乘法。

5.1.2. 运算器

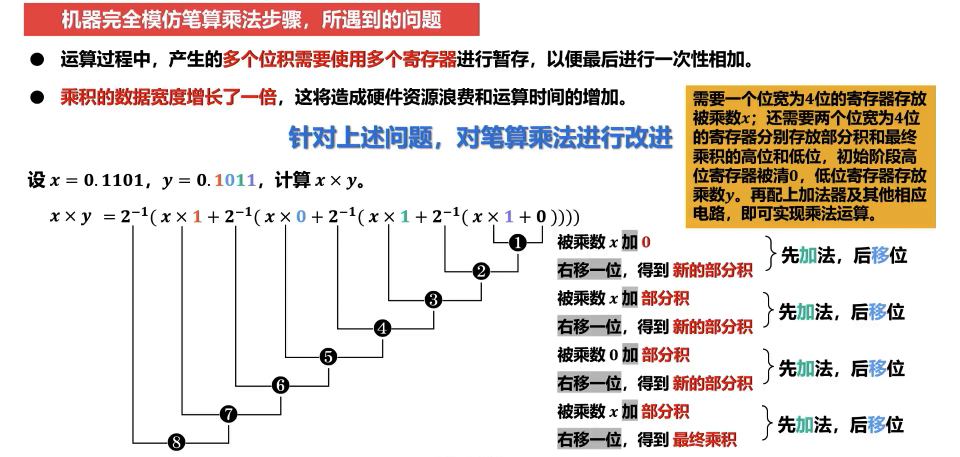
如果 MQ0 等于 0，那么可以省略一次加法

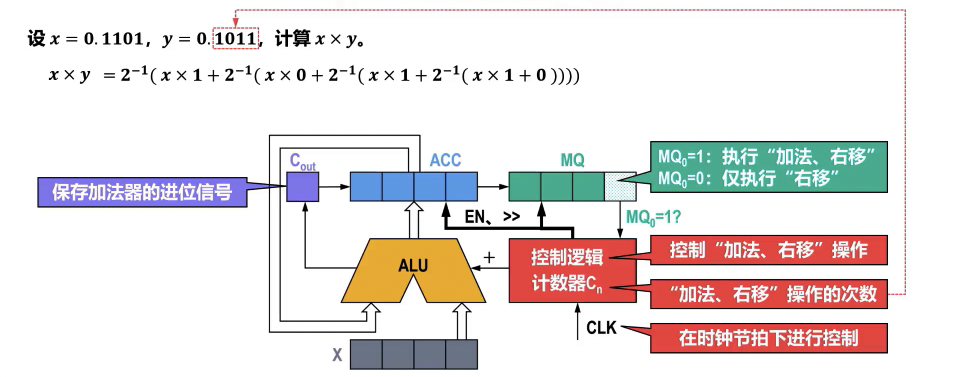
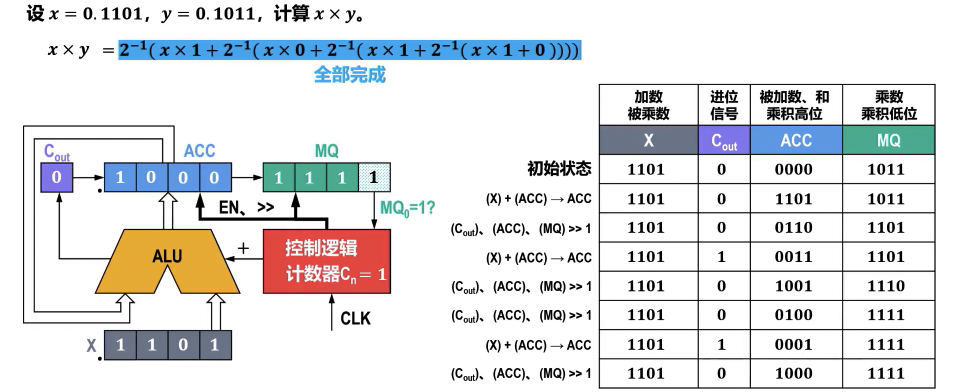
原码一位乘法运算的硬件逻辑实现

• 执行原码绝对值的无符号数一位乘法，最后对符号为进行同或即可

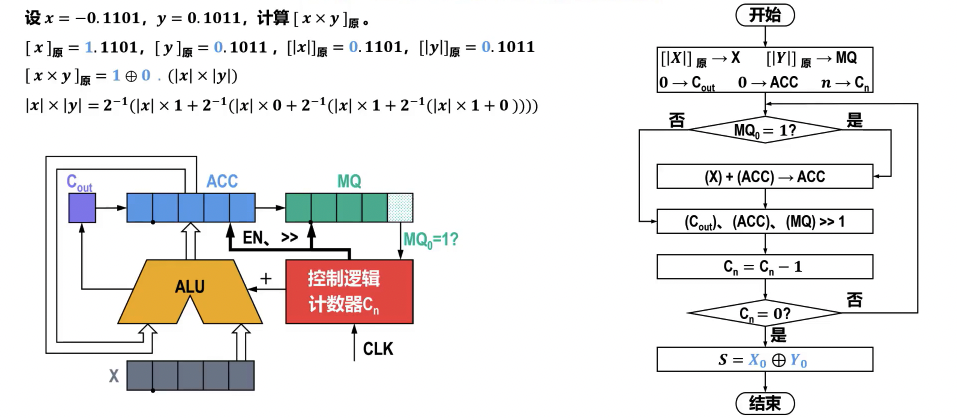
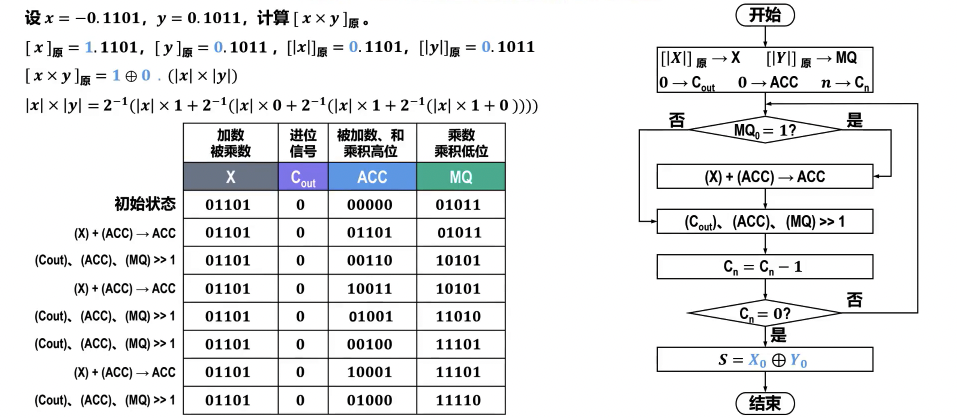
补码乘法运算的硬件逻辑实现

Booth 算法

原理推导

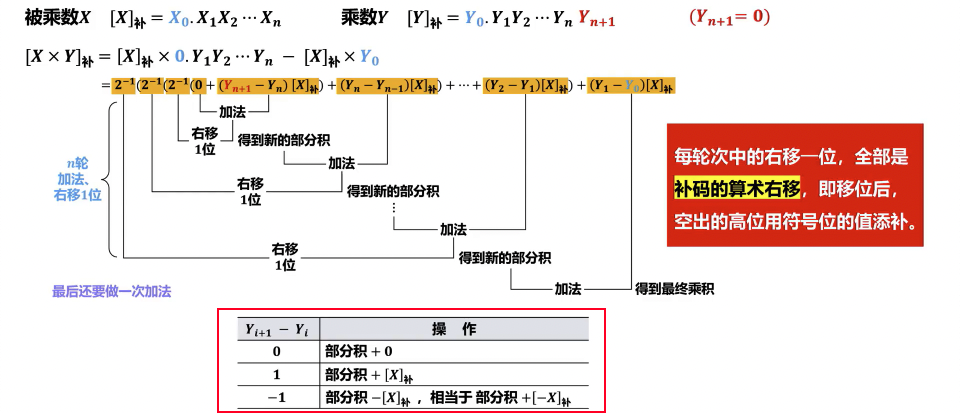
• Booth（布斯）算法：一种高效的补码乘法算法，通过检查当前乘数位 Q0 和附加位 Qn+1 的变化（00, 01, 10, 11）来决定对被乘数 $[X{]}_{补}$ 进行加、减操作或不操作，并进行算术右移。该算法适用于正负数相乘，且结果为补码形式。
• 注意：
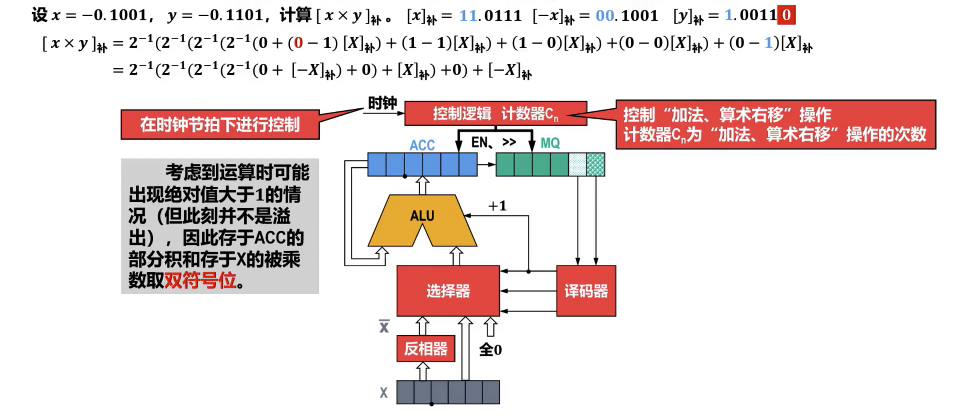
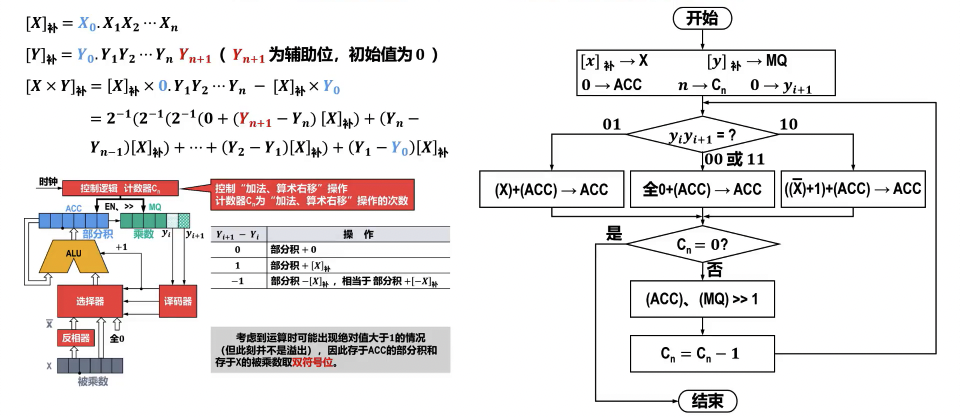
  • 操作数表示：被乘数 $X$ 和乘数 $Y$ 均需转换为补码形式 $[X{]}_{补}$ 和 $[Y{]}_{补}$。
  • 双符号位：计算 $[X\times Y{]}_{补}$ 时，被乘数 $[X{]}_{补}$、乘数 $[Y{]}_{补}$ 以及中间结果（部分积）都需采用双符号位表示，以便在运算过程中判断溢出和确定最终结果的符号。
  • 寄存器初始化：
    • A 寄存器 (ACC, 部分积高位)：初始值为全 0，采用双符号位。
    • Q 寄存器 (MQ, 部分积低位)：存储乘数 $[Y{]}_{补}$，采用双符号位。
    • Qn+1 附加位：初始值为 0。此位与 Q 寄存器的最低位 Q0 共同决定操作。
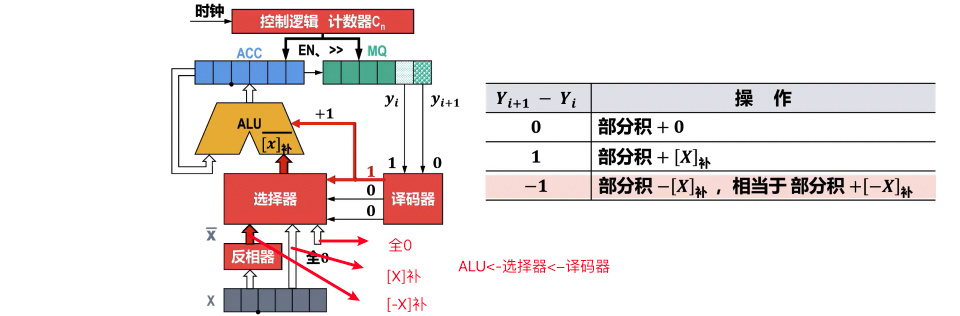
  • 乘法规则（根据 Q0Qn+1）：在每次迭代中，检查 Q 寄存器的最低位 Q0 和附加位 Qn+1
    • 每次操作后，A、Q 寄存器和 Qn+1 位整体进行一次算术右移。
    • 算术右移时，符号位不变，最高位补符号位（双符号位则补两个符号位），最低位舍去。
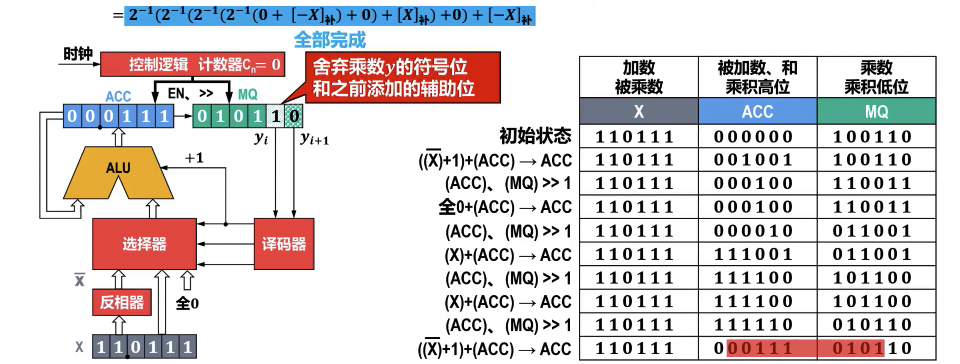
  • 迭代次数：重复上述操作 $n$ 次，其中 $n$ 为乘数有效数值位的位数（不含符号位）。最终结果在 A 寄存器和 Q 寄存器中，为 $[X\times Y{]}_{补}$。
    • 最终结果需要舍弃乘数 $[Y{]}_{补}$ 的符号位和之前添加的辅助位。

Q0Qn+1	操作	意义	移位
00	A + 0	不加不减	算术右移一次
01	A + $[X{]}_{补}$	加被乘数 $[X{]}_{补}$	算术右移一次
10	A + $[-X{]}_{补}$ (即 A - $[X{]}_{补}$)	减被乘数 $[X{]}_{补}$	算术右移一次
11	A + 0	不加不减	算术右移一次

硬件实现

• 原乘数为 4 位，MQ 扩展到 6 位，迭代进行 n 次。则第 5 位为符号位，需舍去。

真题解析

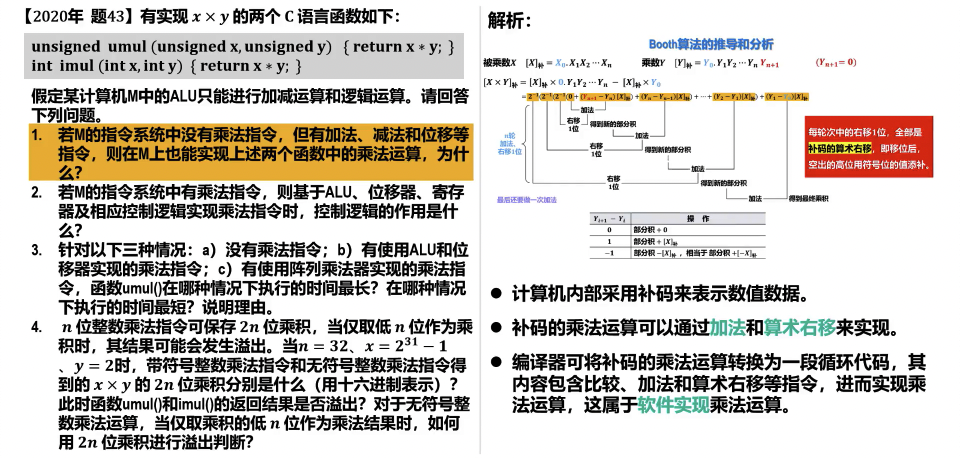
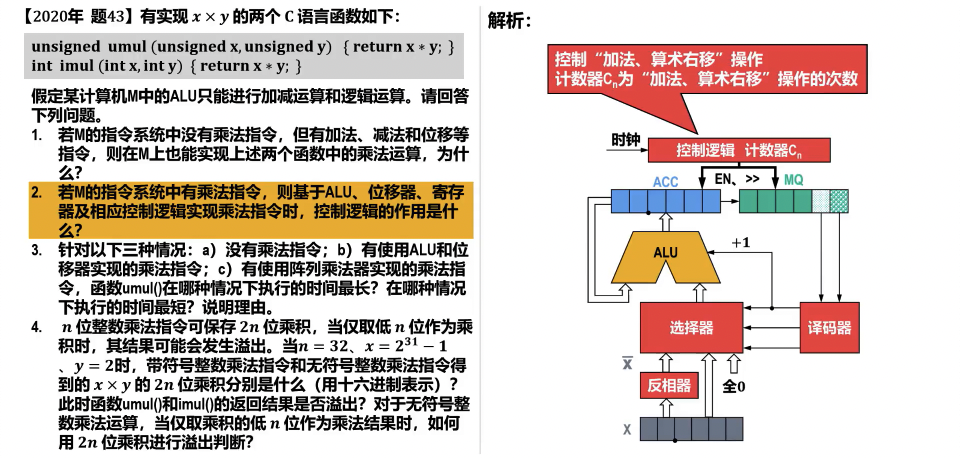
无符号阵列乘法器

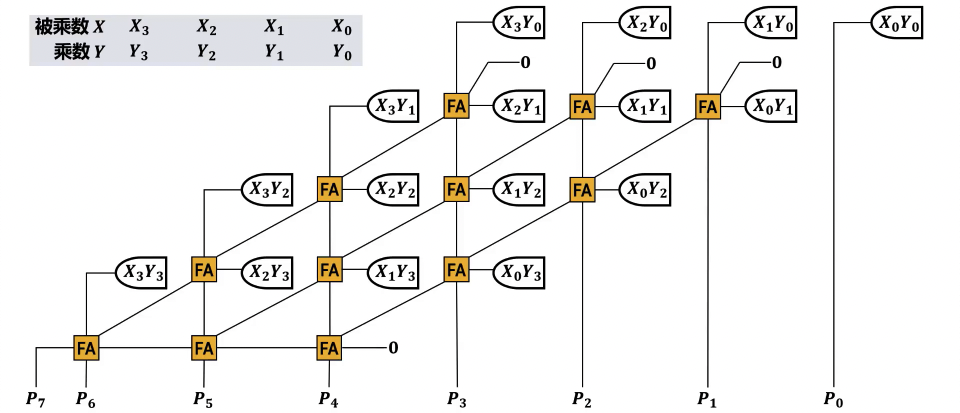
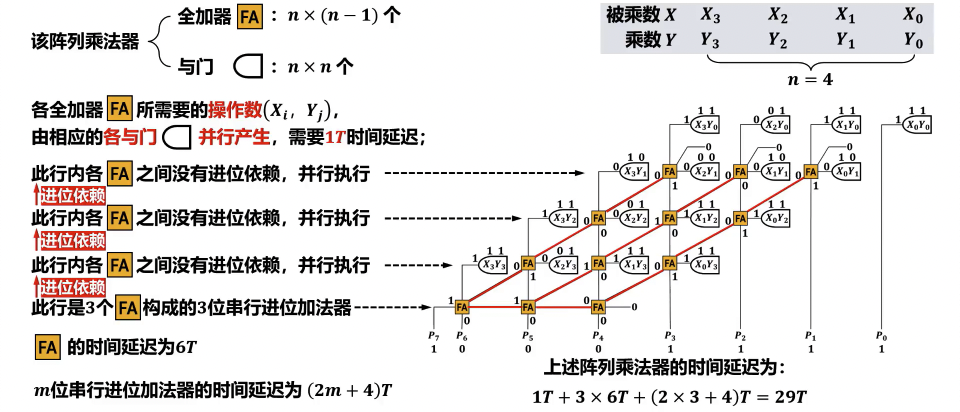
• 由与门和全加器（FA）组成的二维阵列。
  • 结构：通常由 n 行 m 列的与门和约 n*m 个全加器组成，用于 n 位乘数和 m 位被乘数的乘法。
  • 功能分配：
    • 每个与门计算部分积的单个位（P_ij = A_i * B_j）。
    • 每个全加器处理该位及其进位，负责将当前部分积位与其对应的上一级求和结果以及进位进行累加。
• 实现并行计算，速度快，但硬件成本较高。
  • 并行性：所有部分积的生成是并行进行的，部分积的累加也以级联方式并行完成。
  • 速度：乘法时间由阵列中全加器链的延迟决定，通常为 O(n) 或 O(m)，效率高。
  • 硬件成本：需要大量的与门和全加器（约 n*m 个），硬件开销较大。
  • 规则性：结构规整，易于 VLSI (超大规模集成电路) 实现。

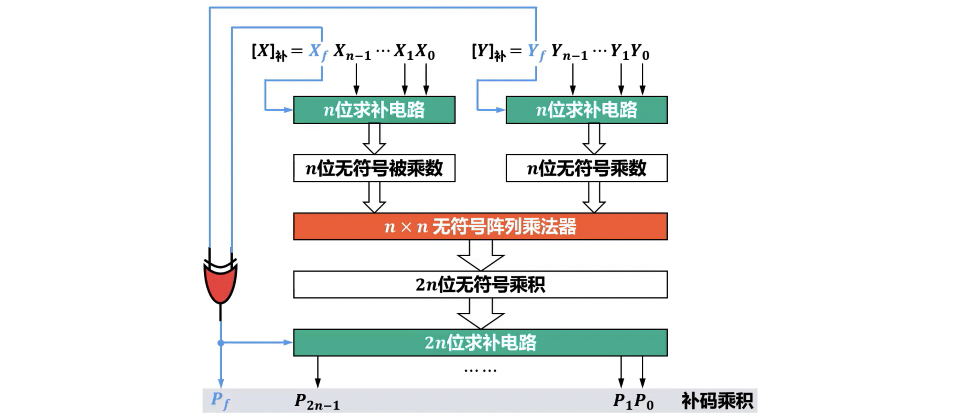
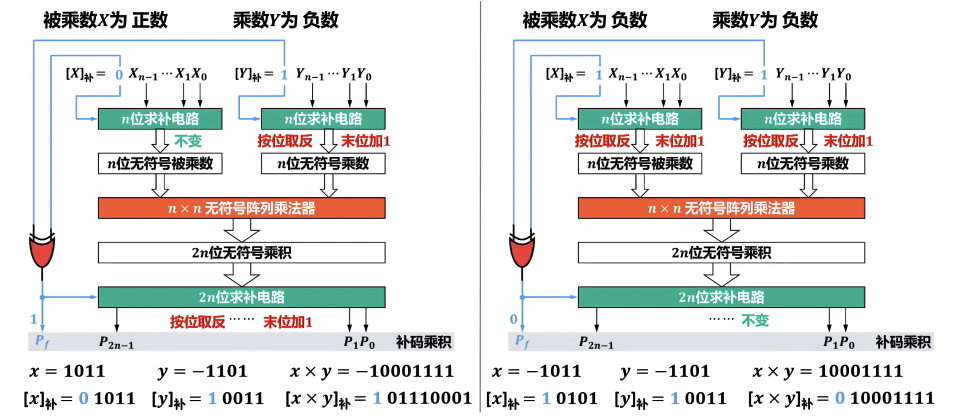
补码阵列乘法器

• 转为原码后使用无符号阵列乘法器运算，单独处理符号位，结果再转回补码