定点数的加法和减法运算
定点数的加法和减法运算通常采用补码形式进行,这使得加法和减法可以使用同一套硬件逻辑实现,简化了设计。补码加减法的核心思想是将符号位和数值位统一处理,并将减法转换为加法。
补码加减法运算公式
- 补码加法
- 公式:[X] 补 + [Y] 补 = [X+Y] 补 (mod 2^(n+1))
- 运算规则:
- 将操作数 X 和 Y 转换为补码表示。
- 将 X 的补码与 Y 的补码的各位(包括符号位)进行二进制加法。
- 最高位(即符号位)产生的进位将自然丢弃。
- 特点:符号位与数值位一起参与运算,运算结果的符号位自动生成。
- 补码减法
- 公式:[X-Y] 补 = [X] 补 + [-Y] 补
- 运算规则:
- 将减法转换为加法,即 X - Y 等价于 X + (-Y)。
- 首先求出被减数 X 的补码 [X] 补。
- 然后求出减数 Y 的补码 [Y] 补,并通过求补运算得到 [-Y] 补。
- 求 [-Y] 补 的方法:对 [Y] 补 的所有位(包括符号位)按位取反,然后在最低位加 1。
- 将 [X] 补 与 [-Y] 补 进行补码加法运算。
- 特点:通过转换为加法,利用加法器实现减法操作。
补码加减法溢出检测
溢出是指运算结果超出了机器所能表示的范围(机器字长)。补码加减法运算中,有多种方法可以检测溢出。
- 双符号位法(变形补码/模 4 补码)
- 表示:用两位符号位表示补码,如 00 表示正数,11 表示负数。
- 检测:
- 当运算结果的双符号位为 01 时,表示 正溢出。
- 当运算结果的双符号位为 10 时,表示 负溢出。
- 当结果的双符号位为 00 或 11 时,表示没有溢出,结果正确。
- 单符号位法(进位判断法)
- 原理:通过比较符号位和最高数值位的进位来判断。
- 符号:
- :符号位向高位(溢出位)的进位。
- :最高数值位向符号位的进位。
- 检测:当 时,表示发生了溢出。
- 若 且 ,表示正溢出(实际值超过了最大正数)。
- 若 且 ,表示负溢出(实际值超过了最小负数)。
- 结果判断法
- 原理:根据操作数的符号和结果的符号来判断。
- 检测:
- 两正数相加,结果为负数,则发生 正溢出。
- 两负数相加,结果为正数,则发生 负溢出。
- 正数与负数相加(或相减),永远不会溢出。
- (注意:这里的“相加”是指代数和,例如 +A + (-B) = A - B,这种情况下不会溢出。)
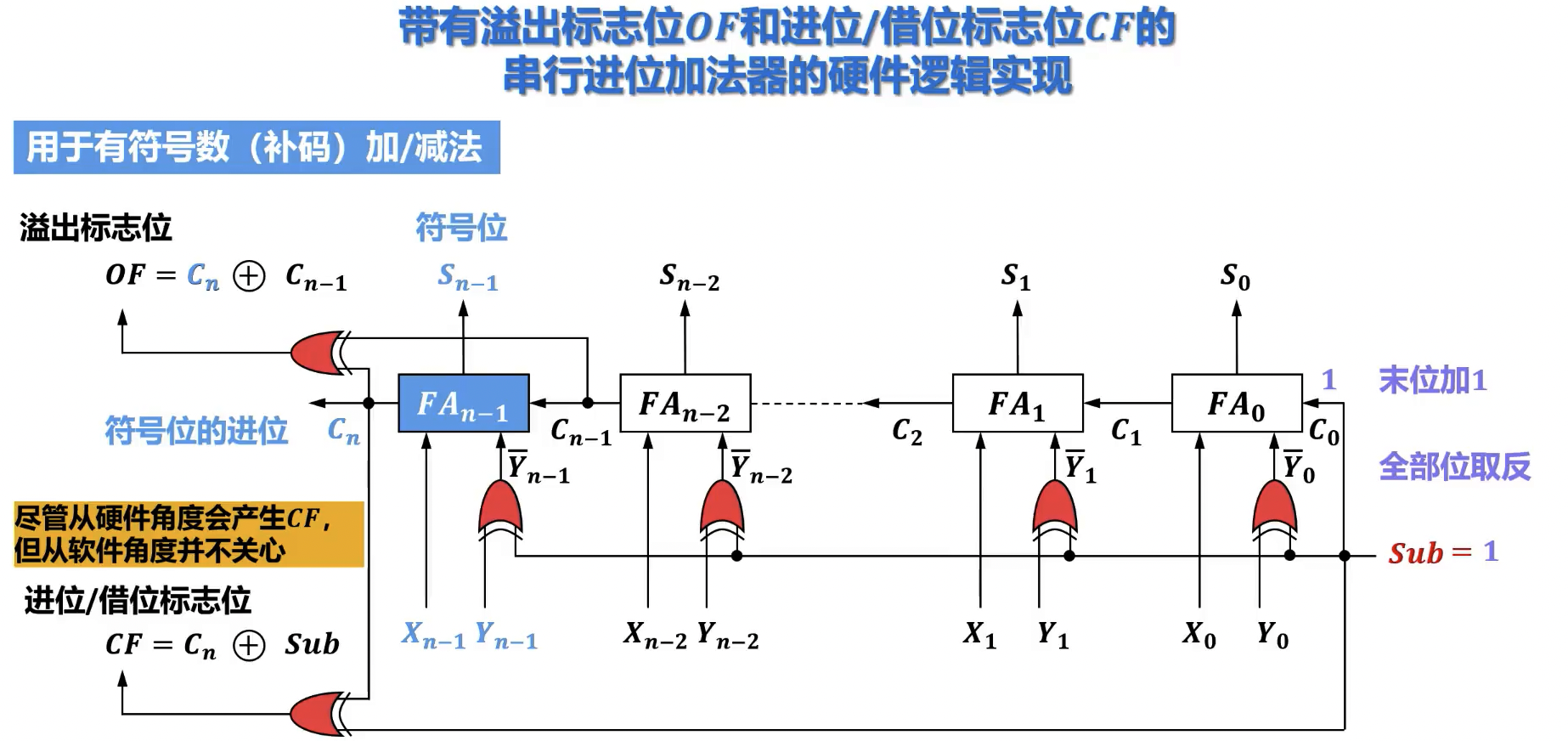
溢出检测的硬件实现
- 硬件实现不关心数值的“有无符号”解释:
- 算术逻辑单元(ALU)在执行加减法运算时,其内部逻辑会根据运算的进位/借位情况,自动生成相关的标志位(如溢出标志 和进位/借位标志 )。
- 这些标志位的生成逻辑是固定的,与数据本身被解释为有符号数还是无符号数无关。它们是运算的“物理”结果。
- 标志 (Overflow Flag):
- 功能:指示有符号数运算结果是否超出了其表示范围。
- 生成逻辑:当最高有效位(MSB)的进位输入 () 与其进位输出 () 不同时, 置 。
- 表达式:。
- 典型情况:
- 两个正数相加,结果为负数。
- 两个负数相加,结果为正数。
- (减法可视为加法:,再分析)
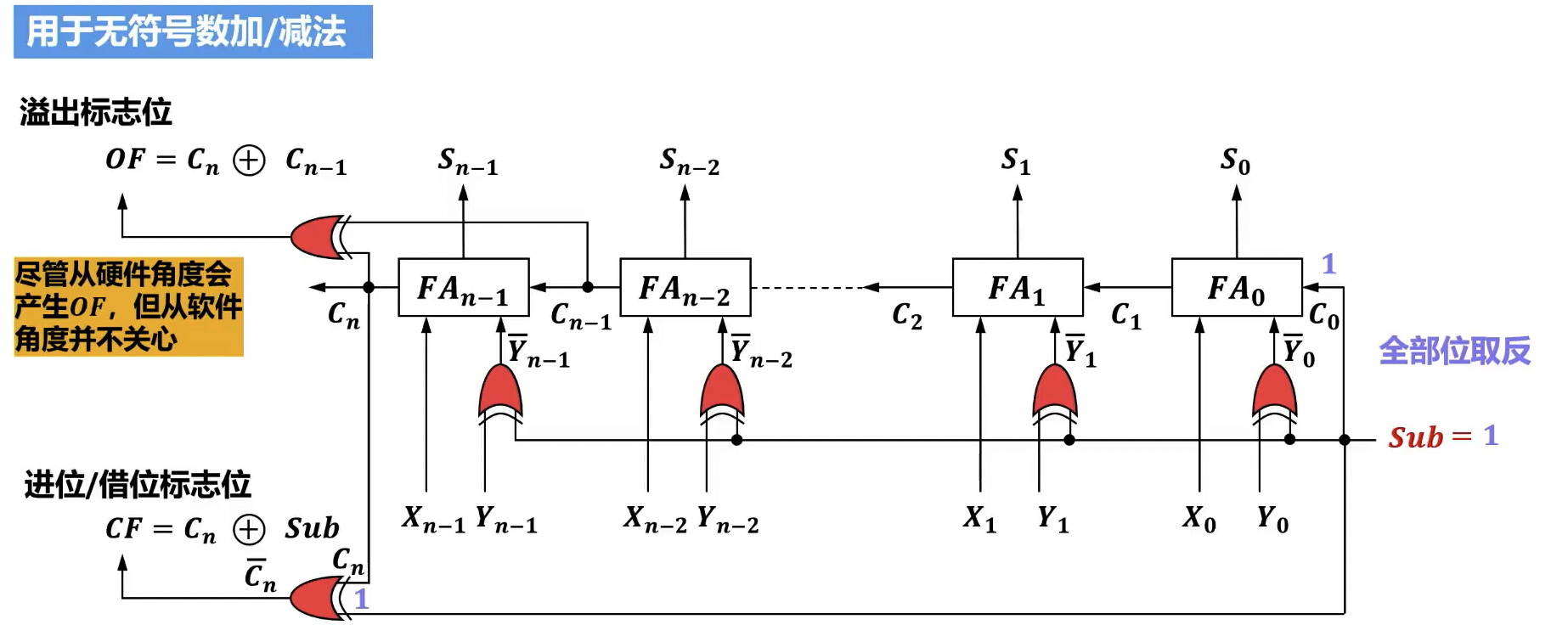
- 标志 (Carry Flag):
- 功能:指示无符号数运算结果是否超出了其表示范围(加法时的进位)或是否需要借位(减法)。
- 生成逻辑:
- 加法: 等于最高有效位(MSB)的进位输出 ()。若 ,表示无符号数加法溢出。
- 减法:对于 ,通常通过 实现。此时, 表示无借位(通常 ,如果最高位有进位)或有借位(通常 ,如果最高位无进位)。在某些处理器中, 表示无借位(), 表示有借位()。
- 典型情况:
- 两个无符号数相加,结果大于其最大表示值。
- 无符号数相减,被减数小于减数。
- 软件视角:
- 软件(如编译器、操作系统或汇编程序)根据数据的约定类型来解释这些硬件生成的标志位,以判断运算结果的有效性。
- 对于有符号数,关心 溢出标志位:
- 表示有符号数运算结果溢出,此时结果不正确。
- 表示有符号数运算结果未溢出。
- 对于无符号数,关心 进位/借位标志:
- 无符号加法: 表示发生进位(即无符号数溢出)。
- 无符号减法: 通常表示发生借位(即被减数小于减数,结果可能需要补码表示或超出无符号数范围)。
逻辑代数和逻辑门
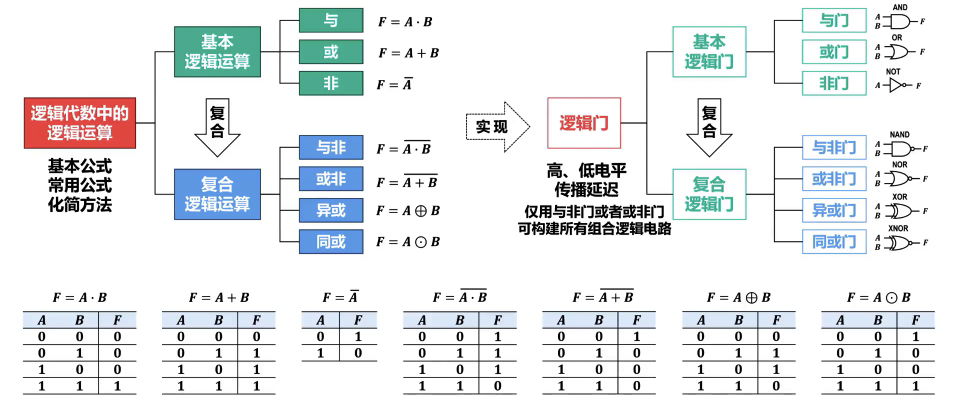
逻辑代数基础
- 基本概念
- 基本运算:
- 与 (AND):逻辑乘,记作 "" 或省略,表示所有条件同时满足。
- 或 (OR):逻辑加,记作 "",表示任一条件满足即可。
- 非 (NOT):逻辑非,记作 "", "" 或 "",表示取反。
- 逻辑常量与变量:只有 0 和 1 两种取值。
- 逻辑函数:描述逻辑变量之间关系的代数表达式。
- 基本运算:
- 基本公理与定律
- 交换律:;
- 结合律:;
- 分配律:;
- 同一律:;
- 零壹律:;
- 互补律:;
- 幂等律:;
- 吸收律:;
- 德摩根定律:;
- 冗余律(消去律):
- 逻辑函数表示方法
- 真值表
- 逻辑表达式
- 逻辑图
- 波形图
- 逻辑函数化简
- 代数法:利用基本定律和公理进行化简。
- 卡诺图法:图形化方法,适用于变量较少(2-4 个)的逻辑函数化简。
- 最小项与最大项
- 圈 0 或圈 1 原则
- 相邻项的合并
常用逻辑门
- 与门 (AND gate)
- 逻辑符号:半圆带平直输入端。
- 逻辑表达式: (或 )
- 特性:只有当所有输入都为高电平 (1) 时,输出才为高电平 (1)。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- 或门 (OR gate)
- 逻辑符号:弯月形输入端,尖头输出端。
- 逻辑表达式:
- 特性:只要有一个输入为高电平 (1),输出就为高电平 (1)。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- 非门 (NOT gate)
- 逻辑符号:三角形带圆圈。
- 逻辑表达式: (或 )
- 特性:输出状态与输入状态相反,只有一个输入端。
- 真值表:
| A | F |
|---|---|
| 0 | 1 |
| 1 | 0 |
- 与非门 (NAND gate)
- 逻辑符号:与门后加圆圈。
- 逻辑表达式: (或 )
- 特性:只有当所有输入都为高电平 (1) 时,输出才为低电平 (0)。通用门:仅用与非门可实现任意逻辑函数。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 或非门 (NOR gate)
- 逻辑符号:或门后加圆圈。
- 逻辑表达式: (或 )
- 特性:只要有一个输入为高电平 (1),输出就为低电平 (0)。通用门:仅用或非门可实现任意逻辑函数。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
- 异或门 (XOR gate)
- 逻辑符号:或门前方加一弧线。
- 逻辑表达式:
- 特性:当两个输入不同时输出为高电平 (1),常用于奇偶校验、半加器。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 同或门 (XNOR gate)
- 逻辑符号:异或门后加圆圈。
- 逻辑表达式:
- 特性:当两个输入相同时输出为高电平 (1),常用于比较器。
- 真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
一位全加器的硬件逻辑实现
用逻辑门电路实现一位加法
- 定义:一位全加器(Full Adder, FA)是实现二进制加法运算的基本组合逻辑电路,能够对两个一位二进制数和一个来自低位的进位输入进行相加,并产生一个和位输出和一个向高位的进位输出。
- 输入:
- : 被加数的第 位
- : 加数的第 位
- : 来自低位的进位 (Carry-in)
- 输出:
- : 和的第 位 (Sum)
- : 向高位的进位 (Carry-out)
- 逻辑表达式:
- 和表达式:
- 进位表达式:
- 等价进位表达式:
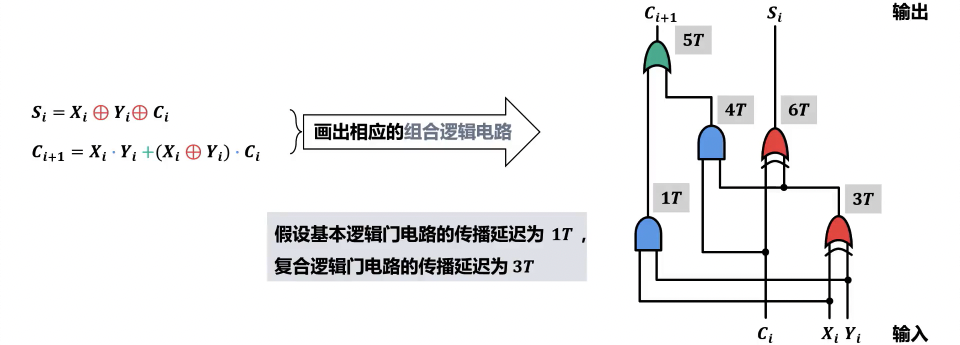
- 全加器
- 功能:对三个一位二进制数(两个操作数和一位进位)进行加法运算,产生一个和位和一个进位位。
- 构成:通常由两个半加器和一个或门(OR gate)构成。具体而言,第一个半加器计算 和 的和及进位;第二个半加器计算第一个半加器的和与 的和及进位;两个半加器产生的进位通过或门组合得到最终的 。
- 应用:是构建多位二进制加法器(如串行加法器、并行加法器,包括行波进位加法器、超前进位加法器等)的基本单元,广泛应用于计算机的算术逻辑单元(ALU)中。
- 半加器
- 功能:对两个一位二进制数进行加法运算,产生一个和位和一个进位位,但不考虑来自低位的进位输入。
- 输入:
- : 第一个操作数
- : 第二个操作数
- 输出:
- : 和 (Sum)
- : 进位 (Carry-out)
- 逻辑表达式:
- 和表达式:
- 进位表达式:
- 限制:由于没有进位输入端,半加器无法直接用于多位二进制数的加法运算,因为它不能处理来自低位的进位信息。
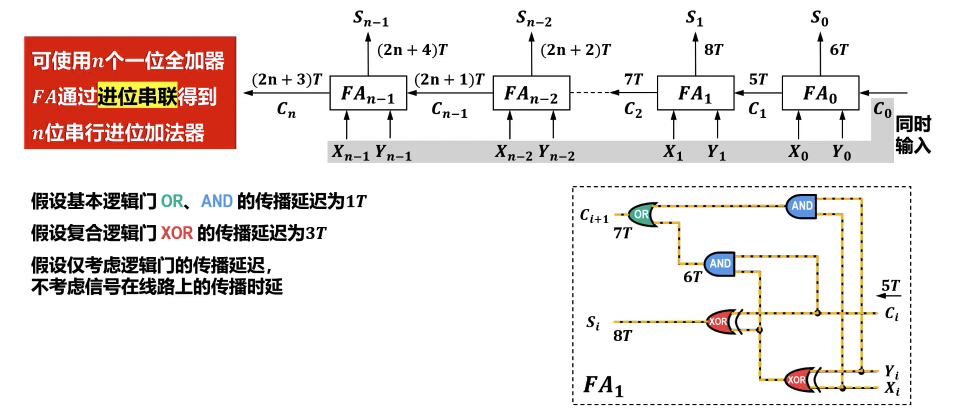
串行进位加法器的硬件逻辑实现
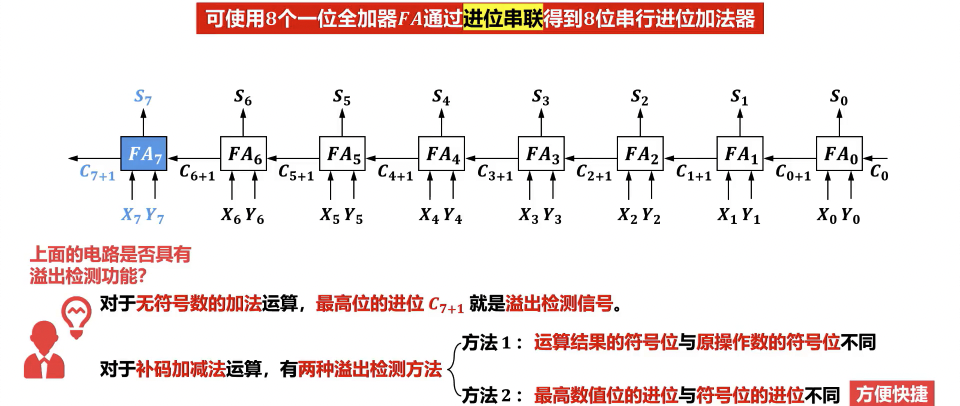

- n 位串行进位加法器
- 基本原理: 由 n 个全加器 (Full Adder, FA) 串联组成。每个全加器处理一位二进制数的加法,并将其产生的进位输出 (Carry Out) 作为下一位(高位)全加器的进位输入 (Carry In)。这种逐位传递进位的方式形成了进位链。
- 结构特点:
- 每个全加器接收两个本位输入位 () 和一个来自低位的进位输入 ()。
- 产生本位的和 () 和向高位的进位输出 ()。
- 优点:
- 硬件结构简单,所需门电路数量较少。
- 易于扩展位数,通过简单地级联全加器即可增加加法器位数。
- 缺点 (主要考点):
- 进位传播延迟 (Carry Propagation Delay):是其最主要的性能瓶颈。由于每一位加法器的计算都必须等待前一位的进位信号,进位信号需要从最低位逐级传播到最高位。
- 计算时间: 如果每个全加器产生进位的延迟为 ,则一个 n 位串行进位加法器的总加法时间近似为 。这导致随着位数 n 的增加,运算速度显著下降。
- 应用: 适用于对运算速度要求不高的场合,或作为其他更复杂加法器(如并行加法器中的子模块)的组成部分。
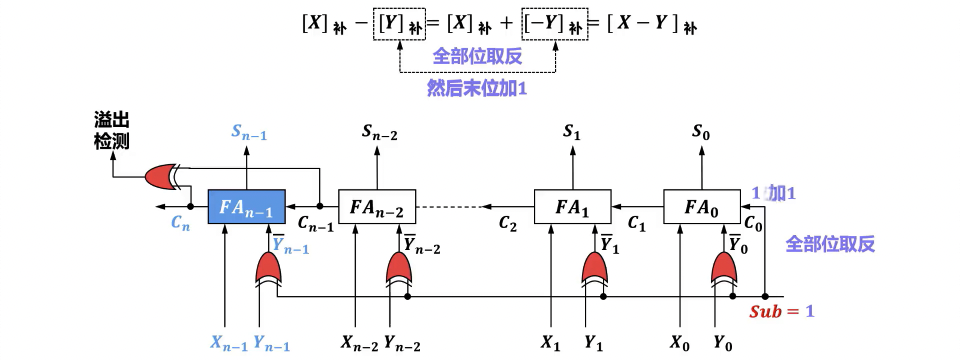
- 改良进位加法器支持补码减法
- 基本思想: 计算机中,减法运算通常通过补码加法实现。即 。在补码表示中, 等于 的反码加 1 ()。通过在加法器输入端增加控制逻辑,可以使同一个加法器既能完成加法也能完成减法。
- 硬件实现:
- 核心组件: 一个 n 位加法器(可以是串行进位加法器,也可以是其他并行加法器)。
- 加/减控制信号 M:
- M = 0 时,执行加法 ()。
- M = 1 时,执行减法 ()。
- 被减数/加数 B 的输入控制:
- 对于 B 的每一位 ,通过一个异或门 (XOR Gate) 与控制信号 M 进行异或运算,生成加法器的实际输入位 。
- 逻辑表达式为:。
- 当 M = 0 (加法) 时,。
- 当 M = 1 (减法) 时, (即 的反码)。
- 最低位进位输入 的控制:
- 加法器的最低位进位输入 直接连接到控制信号 M。
- 当 M = 0 (加法) 时,。
- 当 M = 1 (减法) 时, (用于实现补码中的“加 1”操作)。
- 运算过程:
- 加法 ():
- 加法器实际计算 (因为 为 ,且 )。
- 结果为 。
- 减法 ():
- 加法器实际计算 (因为 为 ,且 )。
- 结果为 ,即 。
- 加法 ():
- 优点: 实现了加减法运算的硬件复用,节省了逻辑门电路资源,是计算机算术逻辑单元 (ALU) 中常用的设计方法。
- 考点: 补码表示及运算规则、加减法统一逻辑的实现、异或门和初始进位在补码减法中的作用。
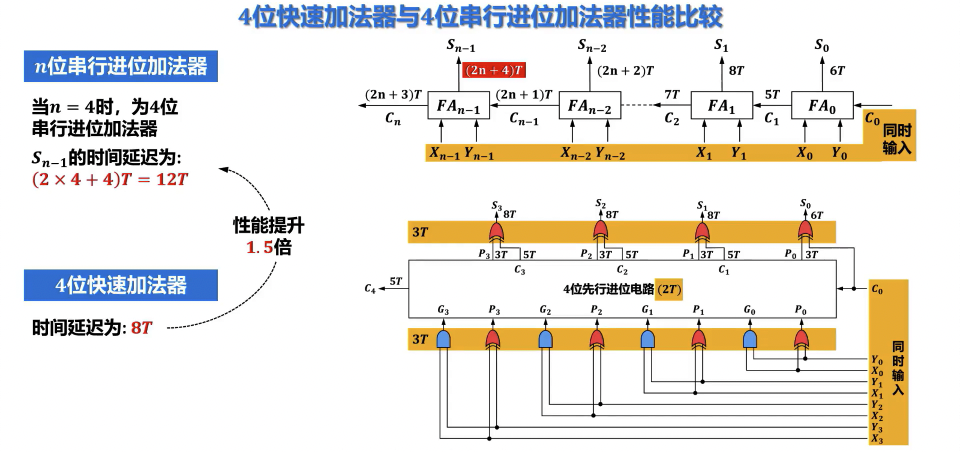
串行进位加法器的性能

先行(并行)进位加法器的硬件逻辑实现
- 目的:解决串行进位加法器中进位信号逐级传递带来的时间延迟问题,提高运算速度。
- 基本原理:通过预先并行计算各位的进位信号,使得每一位的和与进位不再依赖于前一位的实际进位输出,而是直接由输入操作数和初始进位决定。
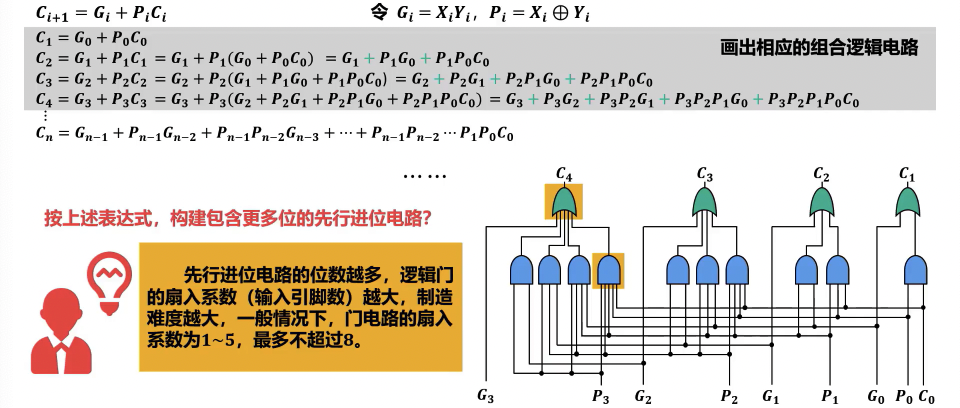
构建先行进位电路
- 进位生成函数
- 定义:表示第 位独立产生进位(无需低位进位)的条件。
- 表达式:
- 物理含义:当被加数 和加数 的第 位都为 1 时,该位会产生一个进位。
- 进位传递函数
- 定义:表示第 位将低位的进位传递到高位的条件。
- 表达式: (或 ,但 更精确地表示仅传递不产生新进位的情况)
- 物理含义:当 和 中只有一个为 1 时,该位会将来自第 位的输入进位 传递到第 位。
- 进位输出 (通常指第 位输出的进位 ,即第 位的输入进位)
- 第 位输出进位 的通用表达式: 其中, 是第 位的输入进位。
- 具体展开式示例 (以 4 位加法器为例,计算 ):
- 说明:所有 和 可以在第一级门延迟内并行计算。随后,所有 可以在第二级或第三级门延迟内并行计算出来,大大减少了进位链的延迟。
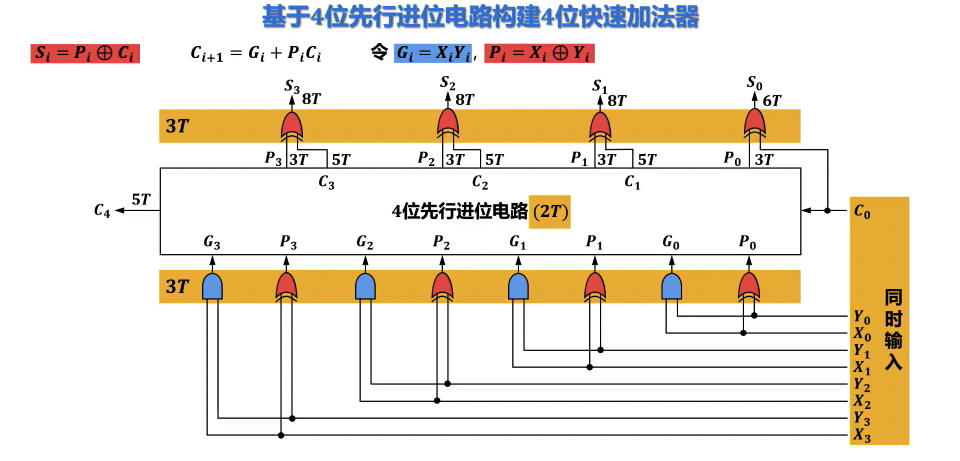
- 总和位 的表达式:
- 优点:
- 高速性:进位产生和传递过程并行进行,加法时间与位数 的对数成正比(或与 无关,取决于具体实现),而非线性相关。
- 适用于大规模集成电路:通过增加硬件复杂度换取运算速度。
- 局限性:
- 硬件复杂度高:随着位数 的增加,实现 的逻辑门输入端数(扇入)和输出端数(扇出)急剧增加。
- 扇入/扇出限制:当位数过多时,单个逻辑门难以满足扇入/扇出要求,需要分块实现或采用多级先行进位结构。
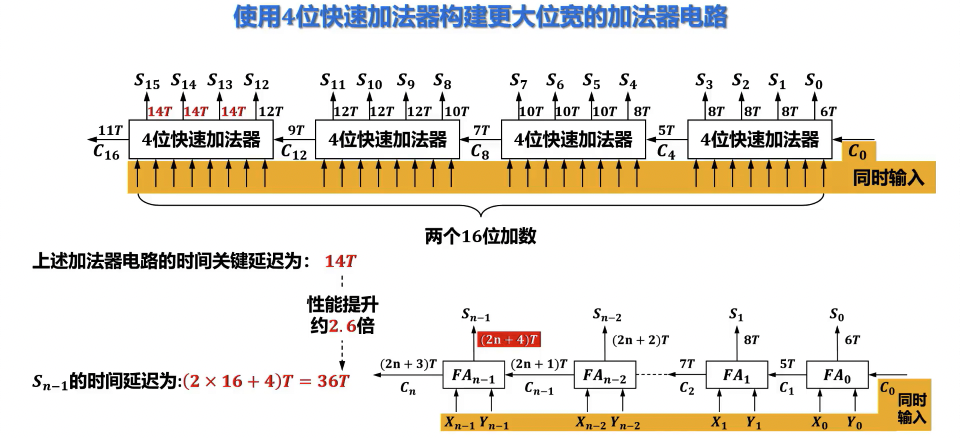
性能比较