定点数的编码表示
原码
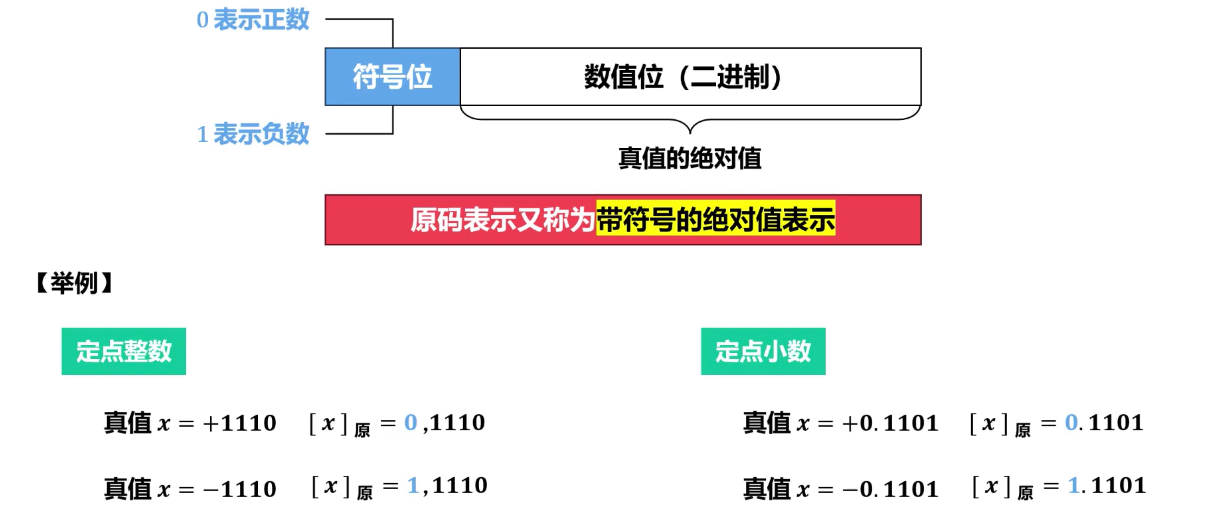
带符号的绝对值表示
- 定义:最高位为符号位(0 表示正,1 表示负),其余位表示数值的绝对值。
- 表示方法:
- 正数:符号位为 0,数值位与真值的绝对值相同。
- 负数:符号位为 1,数值位与真值的绝对值相同。
- 计算举例(以 8 位为例):
- [+5] 原 = 0000 0101
- [-5] 原 = 1000 0101
- 表示范围(n 位):- (2^(n-1) - 1) 到 + (2^(n-1) - 1)。
- 特点:
- 表示直观,易于理解。
- 存在两个零的表示:+0 (00…0) 和 -0 (10…0)。
- 加减运算复杂,需要根据符号位和数值大小进行判断和调整。
- 乘除运算相对简单。
- 应用:仅在浮点数尾码的表示中使用



补码
补数
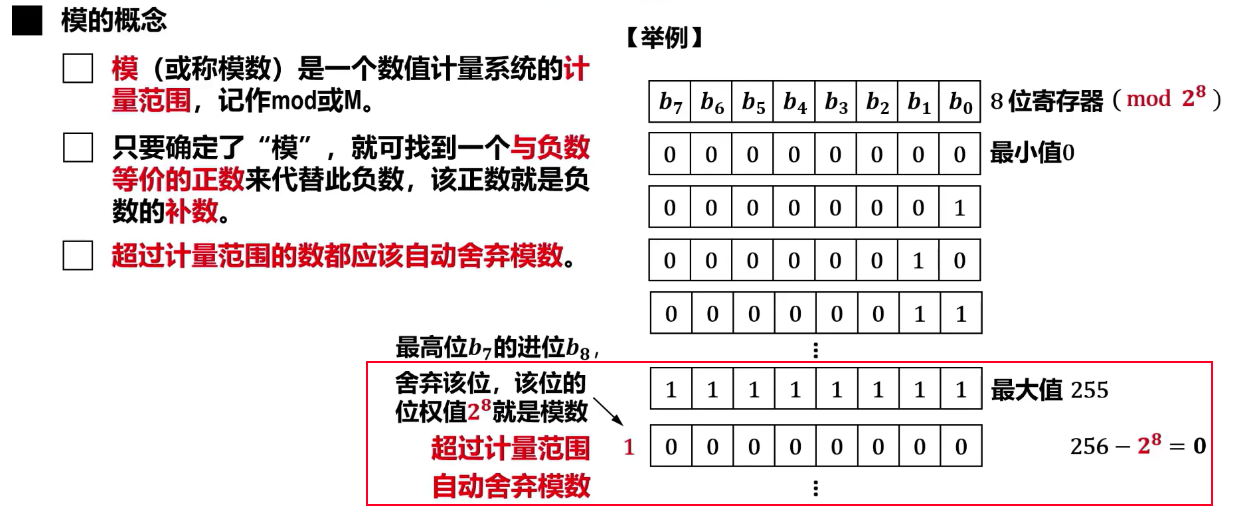
补数的特点
- 一个负数可以用它的正补数来替代,而这个正补数可以用模数加上负数本身求得
- 一个正数和一个负数互为补数时,他们的绝对值之和即为模数
- 正数的补数即该正数本身
补码
- 定义:
- 正数的补码是其本身。
- 负数的补码是其反码加 1。
- 表示方法:
- 正数:与原码和反码相同。
- 负数:符号位为 1,数值位是其绝对值的原码的数值位全部取反后加 1。
- 计算举例(以 8 位为例):
- 补 =
0000 0101 - 补:
- 原 =
0000 0101 - 反 =
1111 1010(符号位不变,数值位取反) - 补 =
1111 1010 + 1 = 1111 1011
- 原 =
- 补 =
- 表示范围(n 位): 到 。
- 特点:
- 只有一个零的表示(00…0)。解决了原码和反码中“0”的重复表示问题。
- 将符号位和数值位统一处理,加减运算可以统一进行(补码加法即为原码加法,补码减法等于补码加补码的负数)。
- 符号为直接参与运算,运算时符号位的进位作为模被自动舍弃。
- 比原码多表示一个最小负数(例如,8 位补码可表示 -128,而原码和反码只能到 -127)。
- 应用:计算机中进行数值运算的标准表示方法。


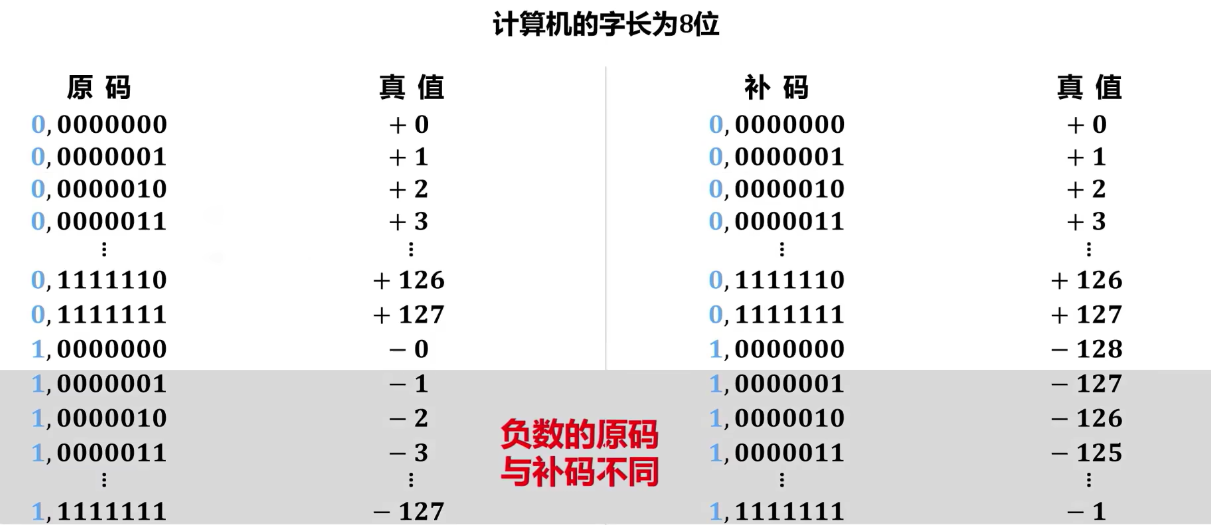
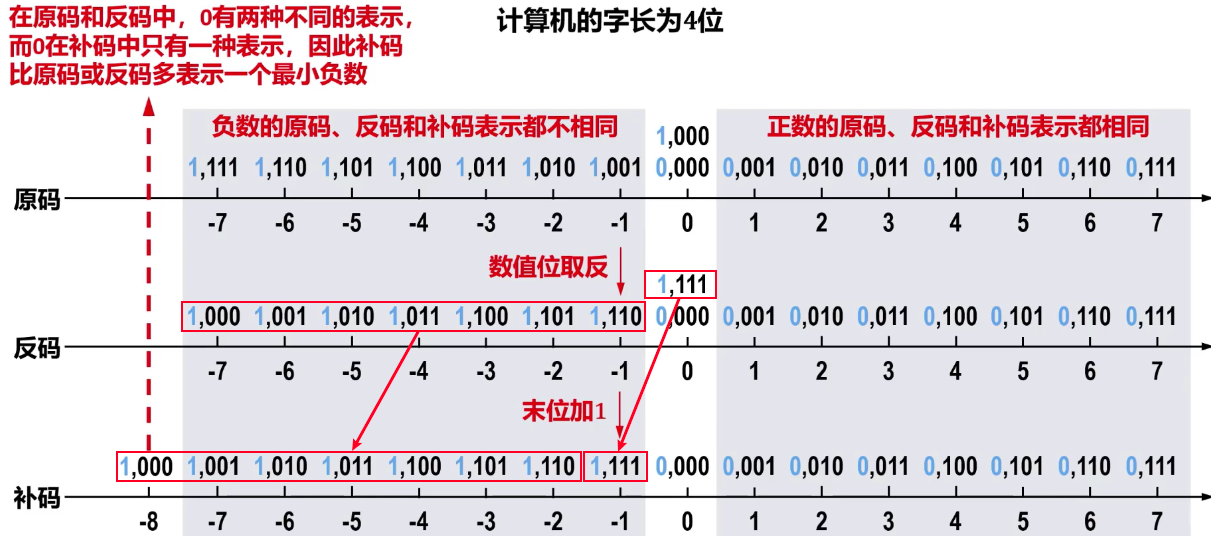
补码和原码区间对比


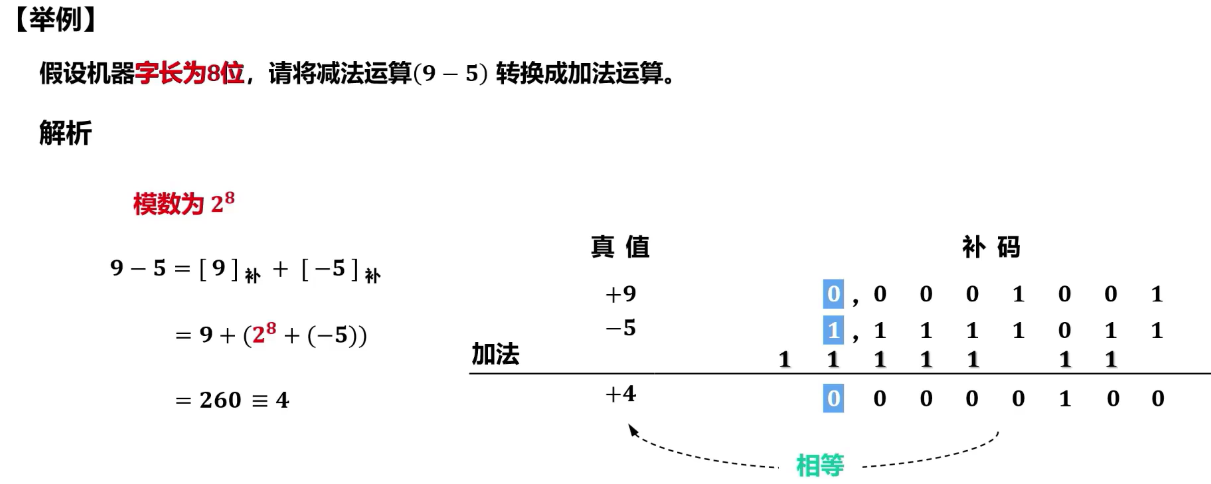
补码加减运算举例
- 将减法转为加法
- 符号位参与运算,进位自动舍弃
反码
- 定义:
- 正数的反码是其本身。
- 负数的反码是其原码的符号位不变,其余数值位取反。
- 表示方法:
- 正数:与原码相同。
- 负数:符号位为 1,数值位是其绝对值的原码的数值位全部取反。
- 计算举例(以 8 位为例):
- 反 =
0000 0101 - 反:
- 原 =
0000 0101 - 反 =
1111 1010(符号位不变,数值位取反)
- 原 =
- 反 =
- 表示范围(n 位): 到 。
- 特点:
- 存在两个零的表示:+0 (00…0) 和 -0 (11…1)。
- 加法运算规则比原码简单,但当最高位有进位时,需要将进位加到最低位(“循环进位”)。
- 应用:早期计算机曾使用,现在主要作为计算补码的中间步骤。


原码、反码和补码的区间差异
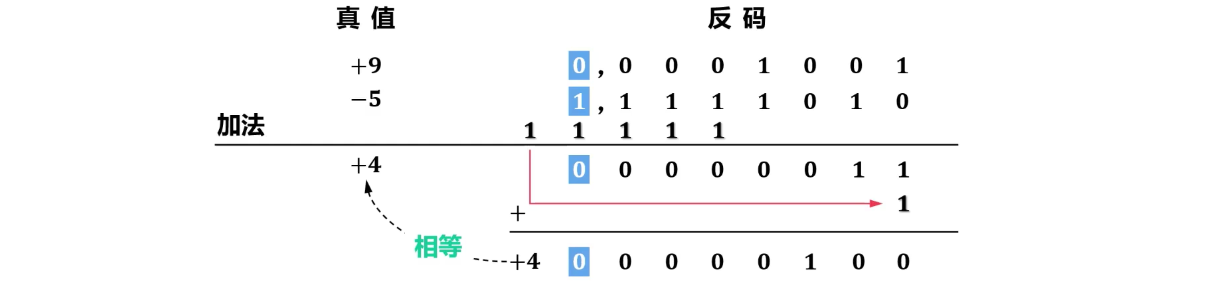
反码加减法运算举例
- 符号位参与运算
- 溢出的符号位需要补到最低位(循环进位)
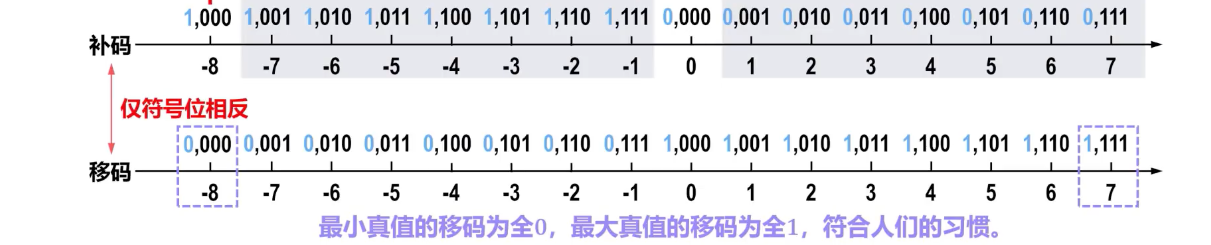
移码
- 定义:真值 X 加上一个偏置量(或称为“偏移量”)K 后得到的编码。通常用于表示浮点数的阶码。
- 表示方法: 移 = X + K。
- 偏置量 K 通常取 或 (对于 n 位移码)。
- 例如,对于 n 位移码,若 ,则真值 0 的移码是 ,即最高位为 1,其余为 0 (10…0)。
- 计算举例(以 8 位,K=128 即 为例):
- 移 = 5 + 128 = 133 =
1000 0101 - 移 = -5 + 128 = 123 =
0111 1011 - 移 = 0 + 128 = 128 =
1000 0000
- 移 = 5 + 128 = 133 =
- 表示范围(n 位, 时): 到 。
- 特点:
- 能够直观地比较大小:移码的大小顺序与真值的大小顺序一致,即移码越大,真值越大。这对于浮点数阶码的比较非常有利。
- 0 的表示是唯一的(当 K=2^(n-1) 时,0 的移码为 100…0)。
- 所有负数的移码的符号位为 0,所有非负数的移码的符号位为 1 (当 时)。这与补码的符号位相反。
- 应用:主要用于浮点数表示中的阶码,便于比较大小。