插入排序
算法思想
插入排序(Insertion Sort)的基本思想是:将一个待排序的记录,按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。
- 核心思想:通过构建有序序列,对未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
- 操作过程:
- 初始时,第一个元素被认为是已排好序的子序列。
- 从第二个元素开始,依次取出每个元素。
- 将取出的元素与已排好序的子序列中的元素从后向前进行比较。
- 如果比待插入元素大的元素,则向后移动一位,直到找到待插入元素的正确位置。
- 将待插入元素插入到该位置。
- 重复上述步骤,直到所有元素都插入到正确的位置。
直接插入排序
算法思想
直接插入排序(Straight Insertion Sort)是一种最简单的插入排序方法。
- 基本步骤:
- 假设前 个元素已经排好序。
- 将第 个元素(待插入元素)插入到前 个有序元素中,使其成为前 个有序元素的一部分。
- 具体做法是:从 元素开始,依次与待插入元素比较。如果当前元素大于待插入元素,则将当前元素后移一位;直到找到第一个小于或等于待插入元素的元素,将待插入元素插入到该元素之后(或之前)。
效率分析
- 时间复杂度:
- 最好情况:当序列已经有序时,每个元素只需与前一个元素比较一次,不需要移动。时间复杂度为 。
- 最坏情况:当序列完全逆序时,每个元素都需要与其前面所有元素比较并移动。时间复杂度为 。
- 平均情况:时间复杂度为 。
- 空间复杂度:(只需要一个额外的空间存储待插入元素)。
- 稳定性:稳定。因为在插入过程中,如果遇到与待插入元素相等的元素,可以选择将其插入到相等元素的后面,从而保持了原有相对次序。
适用性
- 优点:算法简单,易于实现;对于基本有序的序列效率高。
- 缺点:对于大规模无序数据,效率较低,比较和移动次数较多。
- 适用场景:适用于待排序序列数据量较小或基本有序的情况。
折半插入排序
算法思想
折半插入排序(Binary Insertion Sort),又称二分插入排序,是对直接插入排序的改进。
- 改进点:在寻找待插入元素的位置时,不再是顺序查找,而是采用二分查找(折半查找)来确定插入位置。
- 基本步骤:
- 假设前 个元素已经排好序。
- 对于第 个元素(待插入元素),在已排好序的前 个元素中,使用二分查找找到其应该插入的位置。
- 找到位置后,将该位置及之后的所有元素向后移动一位,腾出空间。
- 将待插入元素放入腾出的位置。
- 注意:折半查找只是减少了比较的次数,而元素的移动次数并没有减少。
效率分析
- 时间复杂度:
- 比较次数:由于采用了二分查找,比较次数显著减少,为 。
- 移动次数:与直接插入排序相同,最坏情况下仍为 。
- 总时间复杂度:受移动次数影响,仍为 。
- 空间复杂度:。
- 稳定性:稳定。
适用性
- 优点:减少了比较次数,对于比较操作开销较大的数据类型有一定优势。
- 缺点:元素的移动次数没有减少,因此整体时间复杂度仍然是 。
- 适用场景:与直接插入排序类似,适用于数据量较小的序列,但当比较操作的耗时远大于移动操作时,其优势更为明显。
希尔排序
算法思想
希尔排序(Shell Sort),又称“缩小增量排序”,是直接插入排序的一种更高效的改进版本。
- 核心思想:
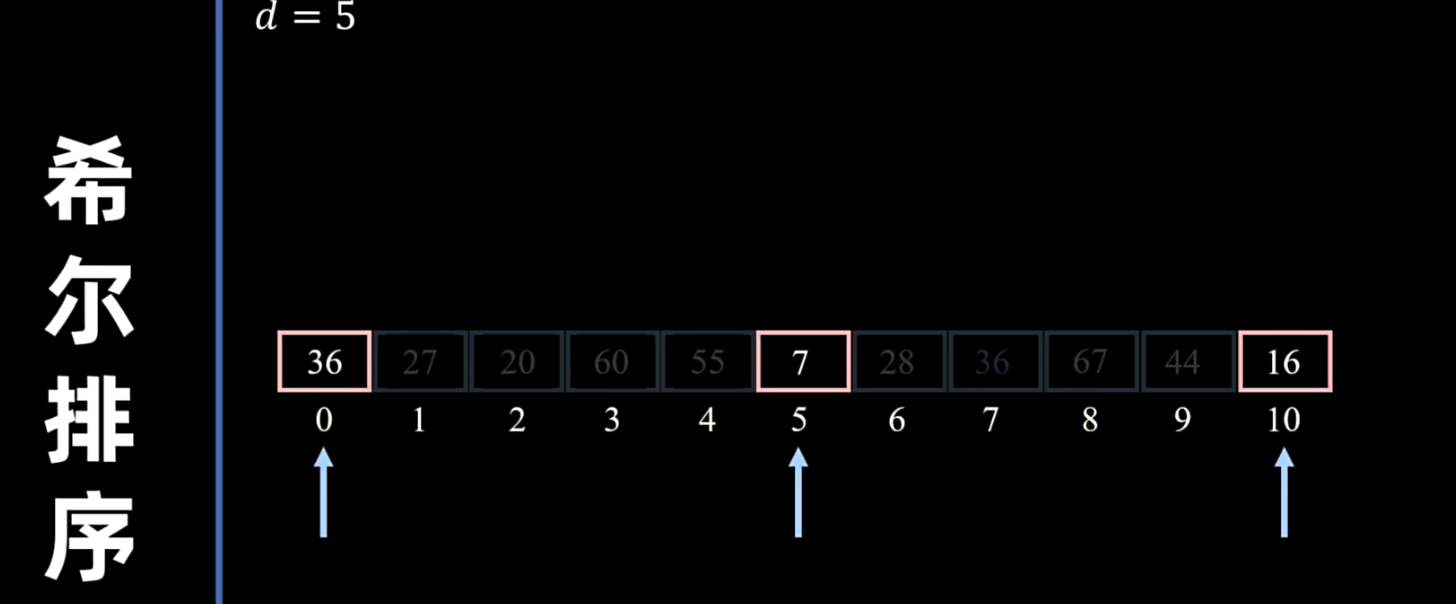
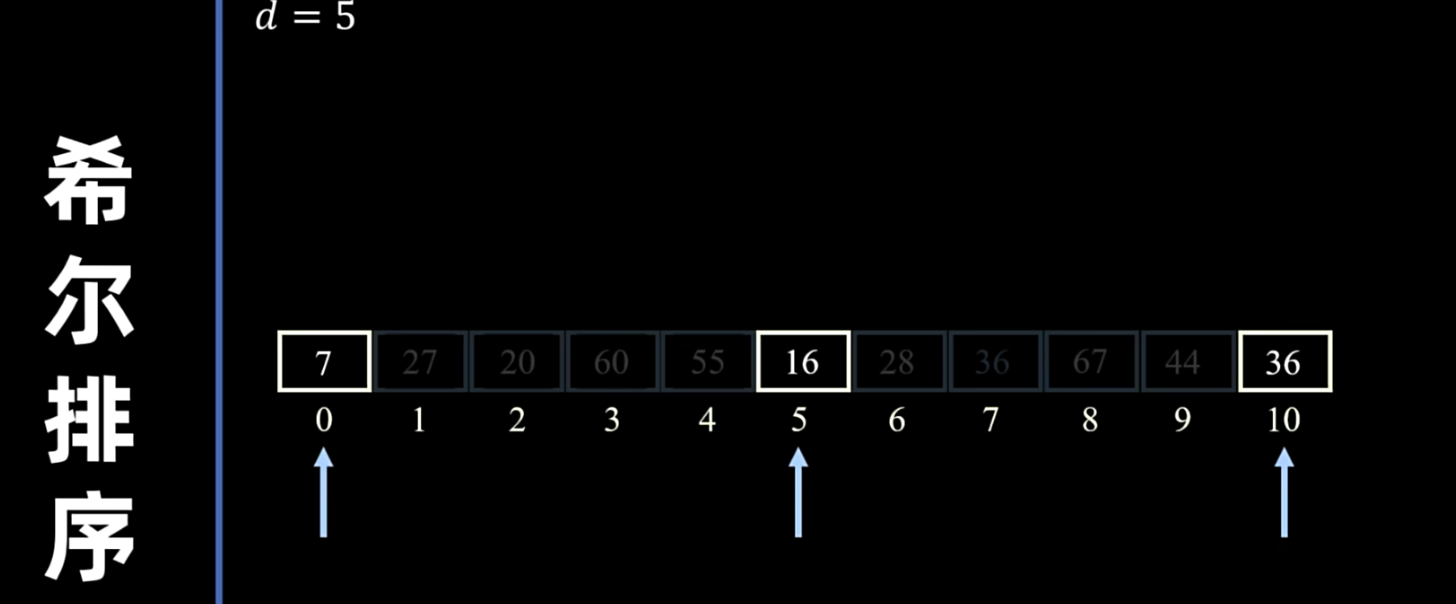
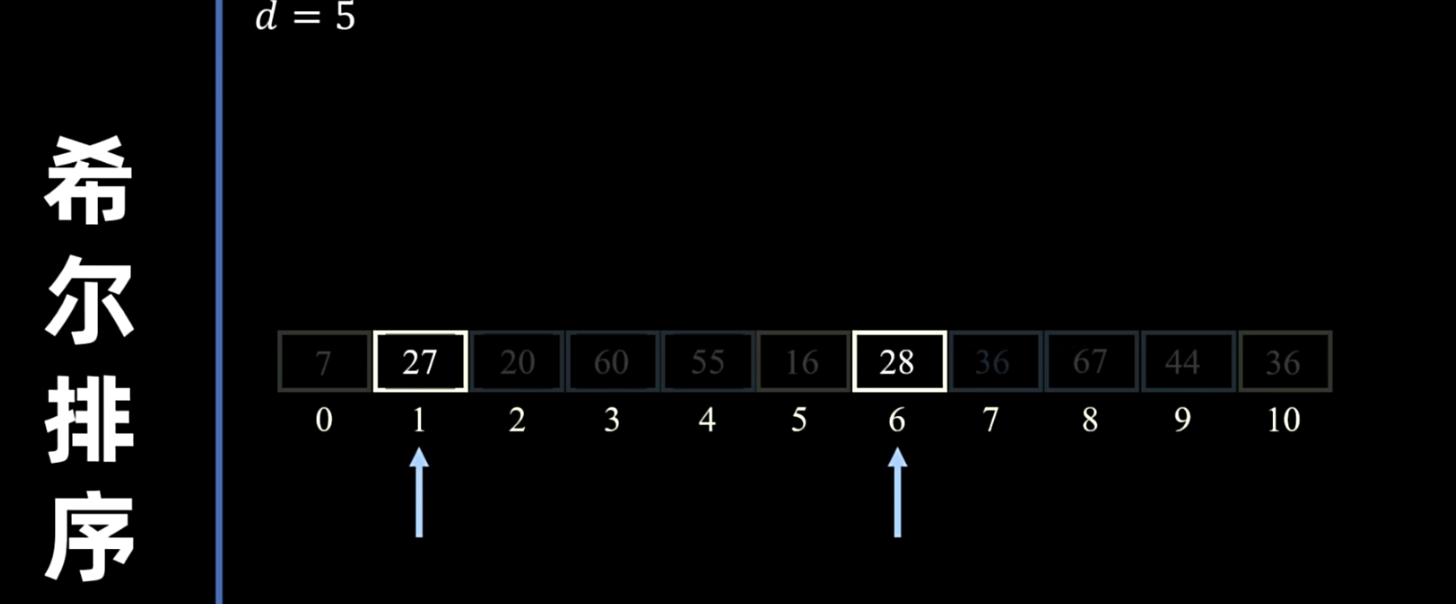
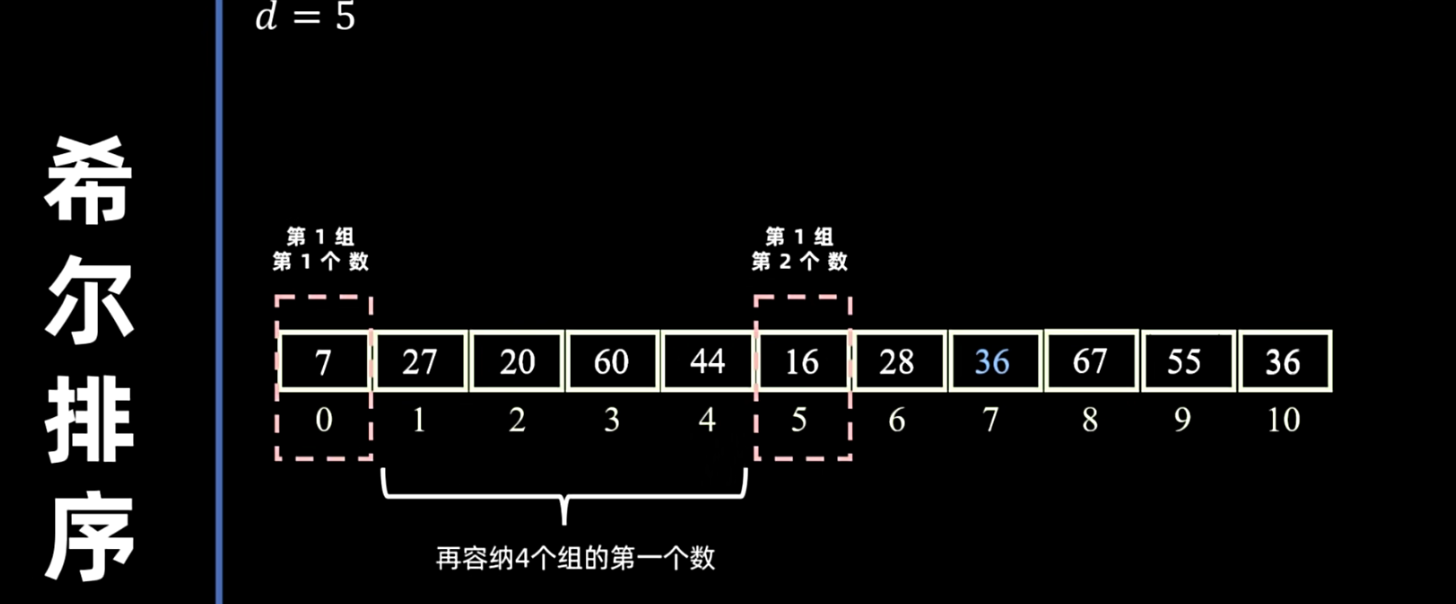
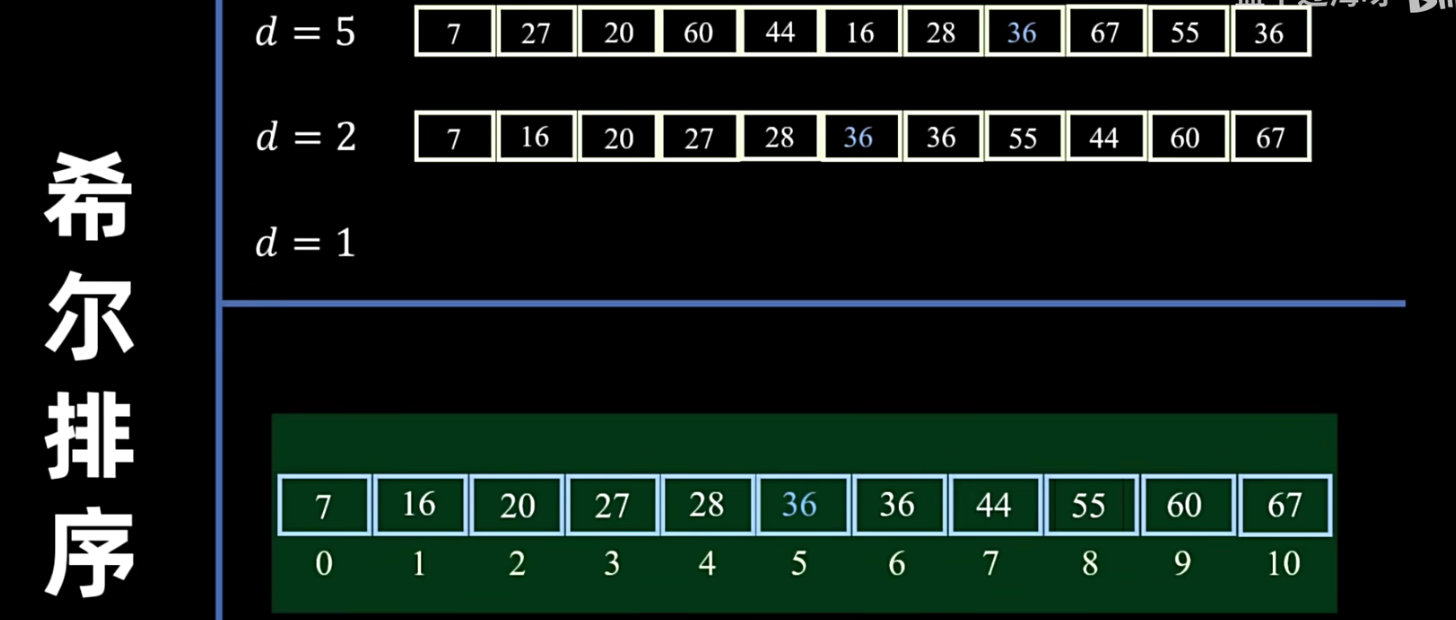
- 分组:将待排序序列划分为若干个子序列,每个子序列由相距某个“增量”(gap)的元素组成。
- 组内插入排序:对每个子序列进行直接插入排序。
- 缩小增量:逐步减小增量,重复上述分组和组内插入排序的过程。
- 最后一次:当增量减小到 1 时,整个序列变为一个子序列,进行最后一次直接插入排序。此时,整个序列已经基本有序,直接插入排序的效率会很高。
- 增量序列的选择:希尔排序的关键在于增量序列的选择。常见的增量序列有:
- (初始增量为 ,每次减半)
- Knuth 序列: ()

效率分析
- 时间复杂度:希尔排序的时间复杂度与增量序列的选择有关,目前没有精确的数学表达式。
- 最好情况: 或 。
- 最坏情况:。
- 平均情况:一般认为在 到 之间,比 快,但比 慢。
- 空间复杂度:。
- 稳定性:不稳定。因为在不同的子序列中,相同关键字的元素的相对位置可能会发生改变。例如,当增量较大时,相等的元素可能被分到不同的子序列中进行比较和交换,导致相对次序改变。
适用性
- 优点:
- 比直接插入排序快得多,尤其对于大规模数据。
- 由于其不稳定性,在某些不要求稳定性的场景下,可以作为快速排序的替代方案。
- 是少数几个能和 算法媲美的 类算法。
- 缺点:算法实现相对复杂,增量序列的选择没有统一标准,对稳定性有要求时不能使用。
- 适用场景:适用于中等规模数据的排序,且不要求稳定性的场景。