图的应用
最小生成树(Minimum Spanning Tree, MST)
核心目标:在一个带权无向连通图中,找到一个包含所有顶点,且边权值之和最小的连通子图(即一棵树)。
应用场景:网络规划(铺设电缆、管道、道路等),以最小成本连接所有节点。
Kruskal (克鲁斯卡尔) 算法
- 核心思想:贪心策略,不断选择当前权值最小的边,只要这条边不形成环,就将其加入 MST。
- 实现原理:
- 将所有边按权值从小到大排序。
- 遍历排序后的边,使用并查集(Disjoint Set Union, DSU) 判断当前边的两个顶点是否已在同一个连通分量中。
- 如果不在同一个连通分量,则合并这两个分量(即加入该边),直到 MST 包含 条边。
- 时间复杂度:,主要消耗在边的排序上。并查集操作(路径压缩和按秩合并优化)可看作近似 。507 并查集
- 适用范围:
- 稀疏图()效率更高。
- 能够处理非连通图,此时会生成一个最小生成森林。
- 优点:概念直观,实现相对简单,尤其适合边列表形式存储的图。
Prim (普里姆) 算法
- 核心思想:贪心策略,从一个起始顶点开始,逐步向外扩展 MST。
- 实现原理:
- 随机选择一个起始顶点,将其加入 MST 顶点集合。
- 在当前 MST 顶点集合与外部顶点集合之间,找到连接这两集合的权值最小的边。
- 将这条边以及边所连接的外部顶点加入 MST。
- 重复步骤 2-3,直到所有顶点都加入 MST。
- 时间复杂度:
- 朴素实现(邻接矩阵,每次线性扫描): 。
- 优化实现(邻接表 + 优先队列/二叉堆): 或 。
- 适用范围:
- 稠密图()时, 的邻接矩阵实现可能优于 Kruskal。
- 必须是连通图(或只考虑一个连通分量)。
- 优点:针对顶点扩展,更适合邻接矩阵或邻接表表示的图。
总结
| 特性 / 算法 | Kruskal 算法 | Prim 算法 |
|---|---|---|
| 工作方式 | 维护边集,逐步添加边,避免形成环 | 维护顶点集,逐步添加顶点,扩展 MST |
| 核心数据结构 | 边集排序、并查集 | 优先队列、邻接表/矩阵 |
| 适用图类型 | 更适合稀疏图 | 更适合稠密图 |
| 处理非连通图 | 可生成最小生成森林 | 只能处理单个连通分量 |
| 时间效率 | (朴素) 或 (优) | |
| 典型应用 | 成本最小化网络连接 | 网络扩展,如从现有网络中心扩展服务 |
最小生成树的唯一性条件
- 不唯一性:最小生成树不一定是唯一的。如果图中存在多条边的权值相同,并且这些边都可以用来连接相同的两个连通分量,那么可能会存在多棵具有相同最小总权值的生成树。
- 唯一性条件:
- 如果图中所有边的权值都互不相同,那么该图的最小生成树是唯一的。
- 证明(举例 Kruskal 算法):当 Kruskal 算法按权值从小到大考虑边时,如果遇到权值相同的边,任意选择一条不形成环的边加入 MST。但如果所有权值都不同,则在每一步选择边时,选择都是唯一的,最终形成的 MST 也是唯一的。
最短路径(Shortest Path)
核心目标:在一个带权图中,找到两个顶点之间权值之和最小的路径。
理论依据:两点之间的最短路径也包含了路径上其他顶点的最短路径。
Dijkstra 算法 (单源最短路径)
- 核心目标:计算从一个指定源点到图中所有其他可达顶点的最短路径。
- 基本思想:贪心策略,逐步确定离源点最近的顶点的最短路径,并用这些已确定的最短路径去“松弛”其邻接点的距离。
- 数据结构:
dist[v]:源点到顶点v的当前最短距离估计值。final[v]:布尔标记,表示顶点v的最短路径是否已最终确定。path[v]:记录最短路径上v的前驱,用于路径回溯。- 通常使用优先队列(最小堆)来高效选择下一个待处理的顶点(未
final且dist最小的)。304 优先队列
- 算法流程(基于优先队列优化):
- 初始化
dist[源点] = 0,其余为 ;所有final为false。 - 将
(0, 源点)放入优先队列。 - 当优先队列不空时:
a. 取出队头元素
(d, u),其中d是当前到u的最小距离。 b. 如果u已经被访问过(final[u]为true),则跳过。 c. 标记final[u] = true,表示u的最短路径已确定。 d. 遍历u的所有邻接点v:如果v未被访问且dist[u] + weight(u,v) < dist[v],则更新dist[v]并将(dist[v], v)放入优先队列。
- 初始化
- 时间复杂度:
- 朴素实现(每次线性扫描找最小):。
- 优先队列优化(邻接表): 或 。
- 适用范围:
- 非负权边的图。如果存在负权边,Dijkstra 算法会失效。
- 单源最短路径问题。
- 局限性:不能处理负权边。
Floyd 算法 (多源最短路径)
- 核心目标:计算图中任意两个顶点之间的最短路径。
- 基本思想:动态规划。通过逐步增加中间顶点的集合来更新所有顶点对之间的最短路径。
- 数据结构:
dist[i][j]:存储从顶点i到顶点j的最短距离。path[i][j]:存储从i到j的最短路径上,经过的第一个中间顶点(用于路径还原)。
- 算法流程:
- 初始化
dist矩阵:对角线为 0,有边连接的为边权,无连接的为 。 - 三重循环:
for k from 0 to n-1(中间点),for i from 0 to n-1(起点),for j from 0 to n-1(终点)。 - 在循环体内,如果
dist[i][k] + dist[k][j] < dist[i][j],则更新dist[i][j] = dist[i][k] + dist[k][j],并更新path[i][j] = path[i][k]。
- 初始化
- 时间复杂度:。
- 空间复杂度:。
- 适用范围:
- 适用于有向图和无向图。
- 可以处理负权边,但不能是负权回路(负权环会导致最短路径无定义)。
- 当要求所有顶点对之间的最短路径时,且顶点数 较小(通常 )时,是高效且易于实现的算法。
- 局限性:时间复杂度较高,不适合大规模图。无法检测负权回路(环)(但会因无限循环而显示异常)。
手工模拟计算
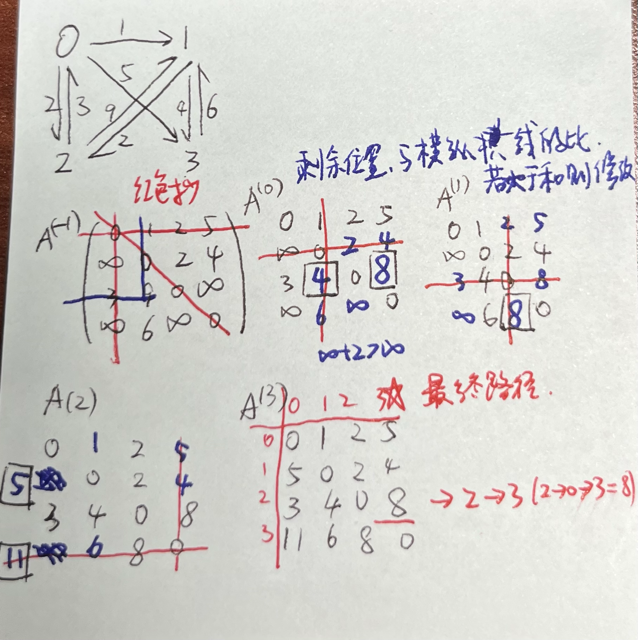
给出矩阵,其中矩阵 A 是邻接矩阵,而矩阵 Path 记录 u,v 两点之间最短路径所必须经过的点 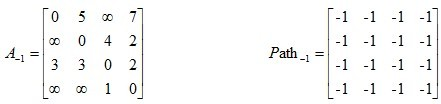 相应计算方法如下:
相应计算方法如下: 


有向无环图
优化包含有公共子式的表达式
- 定义
- 公共子式:在表达式中多次出现的相同子表达式。
- 有向无环图(DAG):一种用于表示表达式的数据结构,其中:
- 结点:表示运算符或操作数。
- 有向边:表示操作数流向运算符。
- 无环:图中不存在任何环路,即不存在从某个结点出发又回到该结点的路径。
- 优化原理
- 通过将公共子式表示为 DAG 中的单个结点,避免重复计算。
- 举例:表达式
(a + b) * (a + b) + c- 传统的语法树会为
(a + b)创建两个独立的子树。 - 使用 DAG,只会为
(a + b)创建一个结点,并让两个乘法运算的输入都指向该结点。 - 这样,
a + b只需计算一次。
- 传统的语法树会为
- 构建 DAG 的方法
- 从左到右扫描表达式:
- 对于每个操作数或运算符,检查是否已存在于 DAG 中。
- 如果存在:重用现有结点。
- 如果不存在:创建新结点。
- 为每个结点关联信息:
- 运算符结点:存储运算符类型及其子结点的指针。
- 操作数结点:存储操作数的值或标识符。
- 可选:为每个结点关联一个“值域”或“结果”信息,表示该结点所代表的子表达式的计算结果。
- 从左到右扫描表达式:
拓扑排序 (Topological Sort)
核心目标:对 有向无环图(DAG) 的顶点进行线性排序,使得对于任意一条有向边 ,顶点 在排序中都出现在顶点 之前。
基于入度的 Kahn 算法 (BFS)
- 核心思想:每次找到并移除图中入度为 0 的节点,将其加入拓扑序列,并更新其邻接点的入度。
- 实现原理:
- 计算所有顶点的入度。
- 将所有入度为 0 的顶点加入队列。如果可选择的入度为 0 的节点多于一个,则拓扑排序不唯一。
- 当队列不空时:
a. 取出队头顶点
u,加入拓扑序列。 b. 对于u的每个邻接点v,将v的入度减 1。 c. 如果v的入度变为 0,则将v加入队列。
- 时间复杂度: ,使用邻接矩阵存储则为 。
- 优点:能够直接检测图中是否存在环(如果最终拓扑序列的顶点数量少于图的顶点数量,则存在环)。
基于 DFS 的算法
- 核心思想:祖先的存在时间必然大于子孙的存在时间。深度优先遍历图,在递归回溯时将顶点加入一个栈或列表。
- 实现原理:
- 对图中的每个未访问顶点进行 DFS。
- DFS 过程中,先递归访问当前顶点的所有邻接点。
- 当一个顶点的所有邻接点都已访问完毕(或无法再向下访问)时,将该顶点压入栈中。
- DFS 结束后,栈中元素的顺序(从栈顶到栈底)就是拓扑序列。
- 时间复杂度:。
- 优点:代码实现通常更简洁。
- 局限性:需要额外的机制来检测环(例如,使用三种颜色标记访问状态:未访问、访问中、已访问)。
拓扑排序的性质与应用
- 唯一性:拓扑排序的结果可能不唯一。如果图中有多个入度为 0 的顶点,或者在处理过程中有多个顶点同时变为入度为 0,则拓扑序列不唯一。只有当图是一条“链”时,拓扑序列才唯一。
- 存在条件:仅存在于有向无环图(DAG)。
- 应用:
- AOV 网中事件的重新编号:
- 根据拓扑排序结果对顶点(活动)进行重新编号,使得所有有向边 都满足 的新编号小于 的新编号。
- 重新编号后,生成的新的邻接矩阵将是一个三角矩阵(通常是上三角矩阵,即所有非零元素 都满足 )。这意味着所有活动 都必须在活动 之前完成。
- 判断有向图是否有环:
- 如果拓扑排序算法(如 Kahn 算法或 DFS)无法将所有顶点都加入拓扑序列,即最终拓扑序列的顶点数小于图的总顶点数,则图中存在环。
- 这是因为环中的顶点在拓扑排序过程中无法被完全处理(例如,它们的入度永远无法变为零)。
- 解决依赖问题:如项目任务的执行顺序、软件模块的编译顺序、课程学习的先修关系、事件的先后顺序等。拓扑排序提供了一个合法的执行序列,确保所有依赖关系得到满足。
- AOV 网中事件的重新编号:
逆拓扑排序 (Reverse Topological Sort)
核心目标:对 DAG 的顶点进行线性排序,使得对于任意一条有向边 ,顶点 在排序中都出现在顶点 之后。
实现方法:
- 基于出度:与 Kahn 算法类似,但从出度为 0 的顶点开始,并使用逆邻接表或在邻接表上反向操作。
- 基于 DFS:直接使用 DFS 算法,但将顶点压入栈的顺序改为在递归进入时压栈,或者在 Kahn 算法中找到入度为 0 的节点时,将它从正向邻接表中删除,然后从逆向邻接表中找到出度为 0 的节点。最常见且简单的实现是:执行一次普通拓扑排序,然后将得到的序列逆序。
应用场景:
- 解决“谁依赖我”的问题,例如:一个任务完成后,有哪些任务可以开始。
- 某些动态规划问题在 DAG 上的求解。
关键路径 (Critical Path Method, CPM)
核心目标
在 AOE 网(Activity On Edge Network) 中,找出从起点到终点耗时最长的路径,这条路径决定了整个项目完成的最短时间。
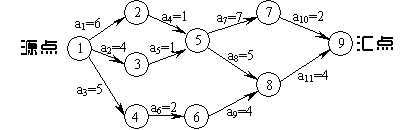
AOE 网概念
- 顶点(事件):表示某个活动完成的瞬间,或某个条件达成。
- 边(活动):表示一项需要时间和资源的任务。边的权值是活动的持续时间。
关键活动与关键路径
- 关键活动:时间余量为 0 的活动(即 )。这些活动一旦延误,将直接导致整个项目工期延长。
- 关键路径:由一系列关键活动组成的路径。一个 AOE 网可能有多条关键路径。
关键参数
- 事件最早发生时间 ( / ):事件在不延迟任何后续活动的前提下能够发生的最早时刻。
- 事件最晚发生时间 ( / ):事件在不延迟整个项目工期的前提下可以发生的最晚时刻。
- 活动最早开始时间 ( / ):活动能够开始的最早时刻,等于其起点的 。
- 活动最晚开始时间 ( / ):活动在不延迟整个项目工期的情况下,能够开始的最晚时刻。等于其终点的 减去活动持续时间。
- 活动时间余量 ():。表示活动在不影响总工期的情况下可以拖延的时间。
算法流程
- 构建 AOE 网络:将项目活动和依赖关系建模为带权有向图。
- 计算事件最早发生时间 ():
- 对图进行拓扑排序。
- 按照拓扑序列,从前向后计算每个事件的 。
- ,其中 是所有指向 的前驱事件。
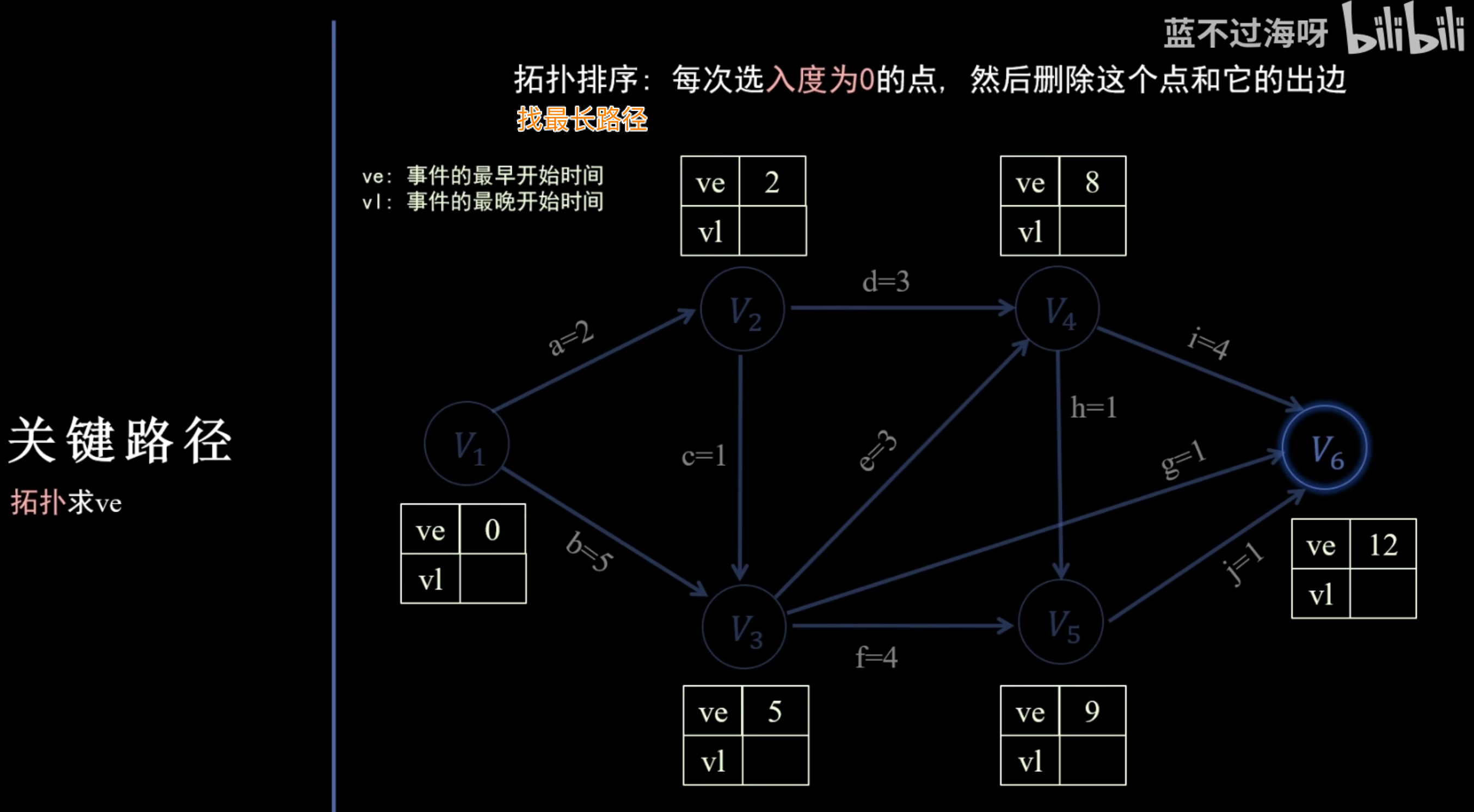
- 计算事件最晚发生时间 ():
- 确定终点事件的 等于其 (即总工期)。
- 按照逆拓扑序列,从后向前计算每个事件的 。
- ,其中 是所有从 出发的后继事件。
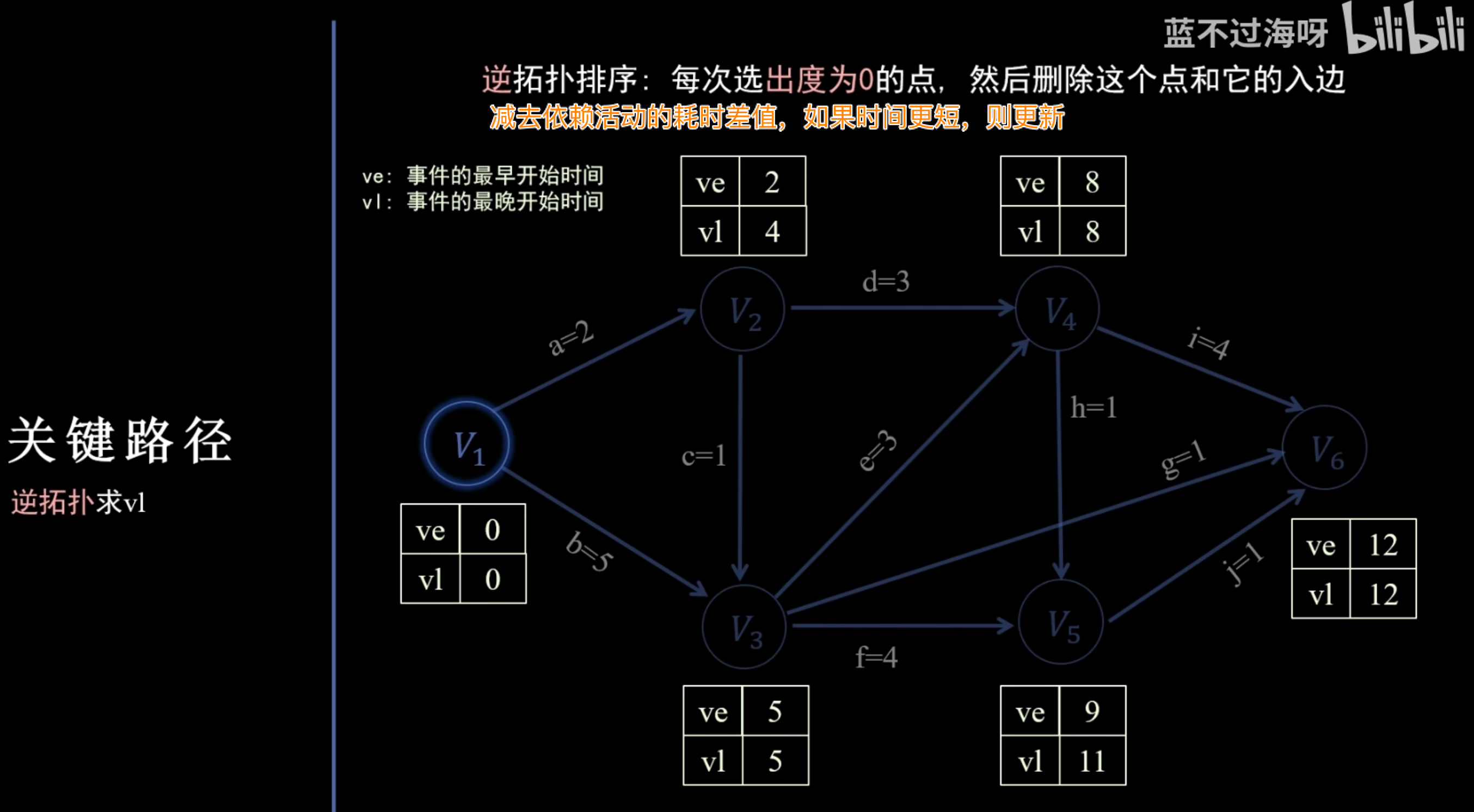
- 计算活动最早/最晚开始时间并判断关键活动:
- 对于每条活动边 权值为 :
- 如果 ,则活动 是关键活动。
- 活动时间余量 ():。表示活动在不影响总工期的情况下可以拖延的时间。
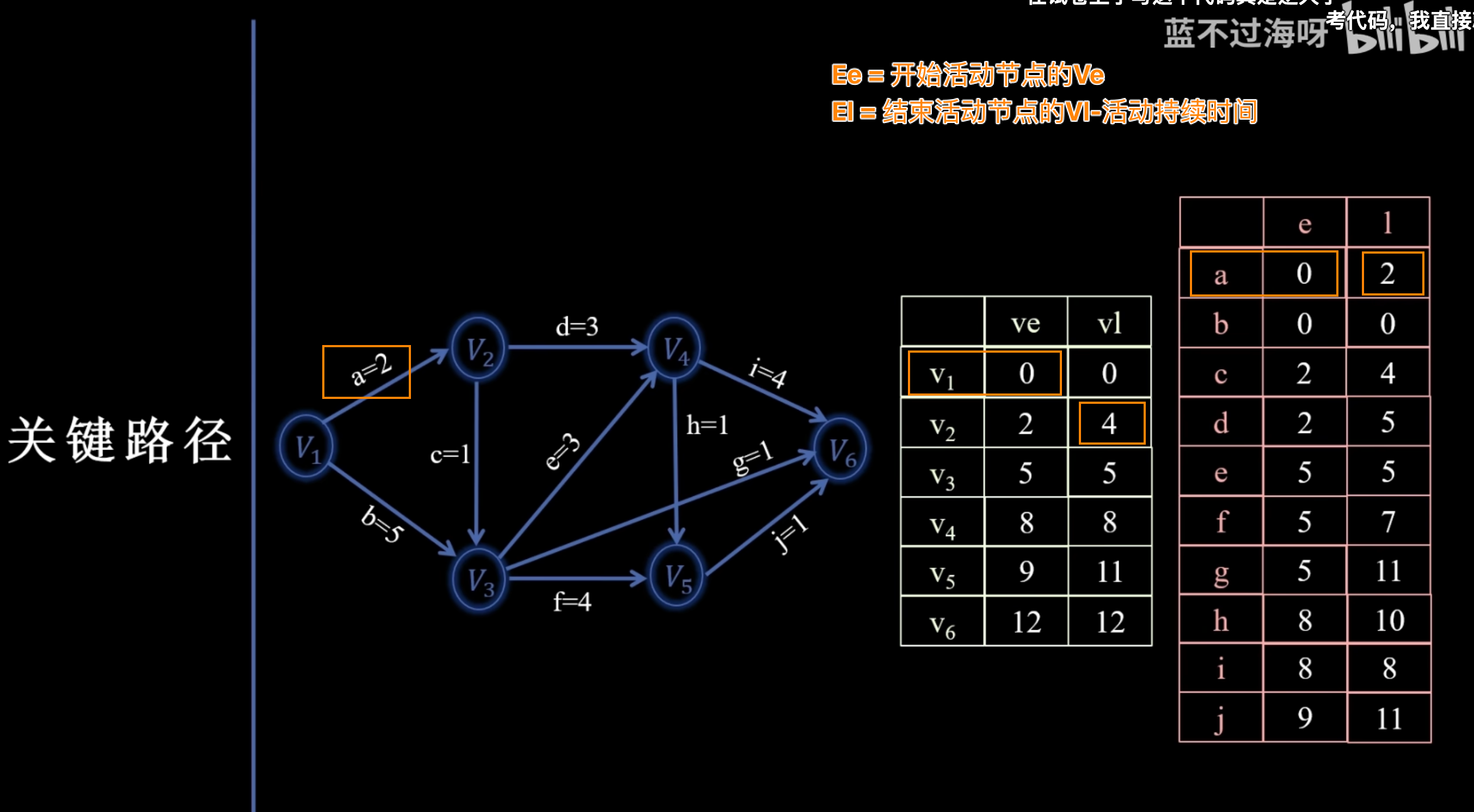
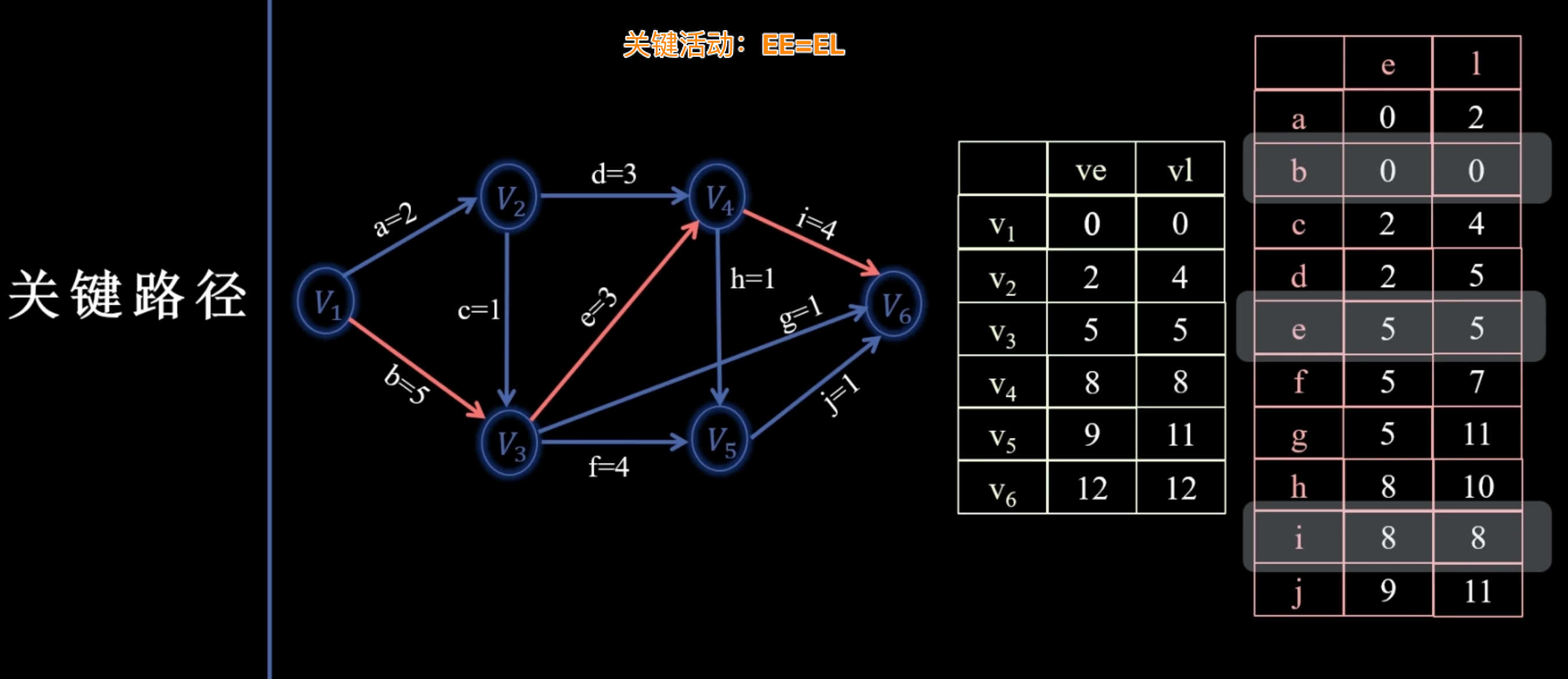
- 对于每条活动边 权值为 :
- 识别关键路径:将所有关键活动连接起来,形成一条或多条从起点到终点的路径,这些路径就是关键路径。
重要特性
- 总工期:AOE 网络的总工期等于终点事件的 和 。
- 缩短工期:只有缩短关键路径上的活动持续时间才能缩短总工期。
- 多条关键路径:若存在多条关键路径,则必须同时关注所有关键路径上的活动。