504 树的存储结构

树的存储结构

树作为一种非线性数据结构，可使用顺序存储或链式存储表示。根据不同的应用需求，有多种存储方法可供选择。

双亲表示法

基本思想

利用树中每个结点（除根结点外）有唯一双亲的特点，用一维数组存储树中各结点，每个结点除存储数据外，还存储其双亲结点在数组中的位置。

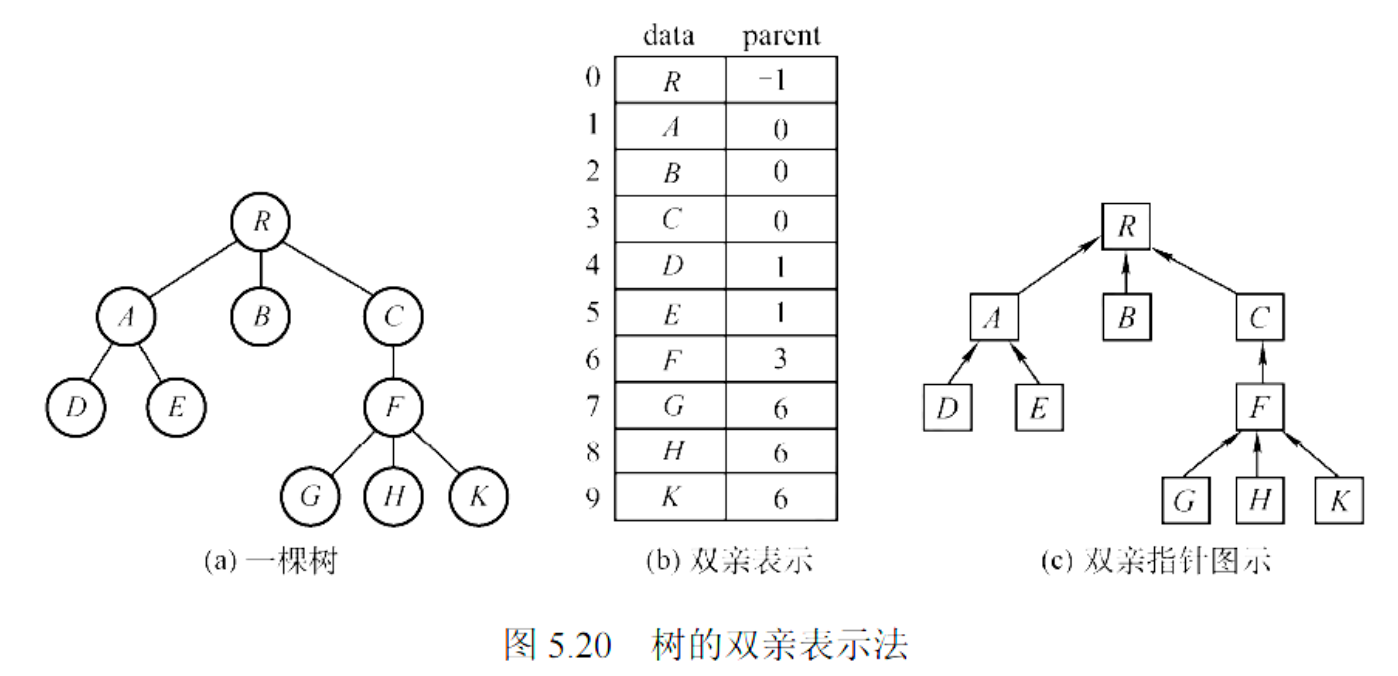
存储结构

typedef struct {
    ElemType data;    // 结点数据
    int parent;       // 双亲结点的数组下标
} PTNode;
 
typedef struct {
    PTNode nodes[MAX_SIZE];  // 结点数组
    int n;                   // 结点个数
} PTree;

特点分析

• 优点：可以直接得到一个结点的双亲，查找双亲操作时间复杂度为 O(1)
• 缺点：求结点的孩子需要遍历整个结构，时间复杂度为 O(n)
• 适用场景：适合需要频繁查找双亲结点的应用

孩子表示法

基本思想

把每个结点的孩子结点排列成一个线性表，以单链表存储。n 个结点有 n 个孩子链表，如果是叶子结点则此单链表为空表。

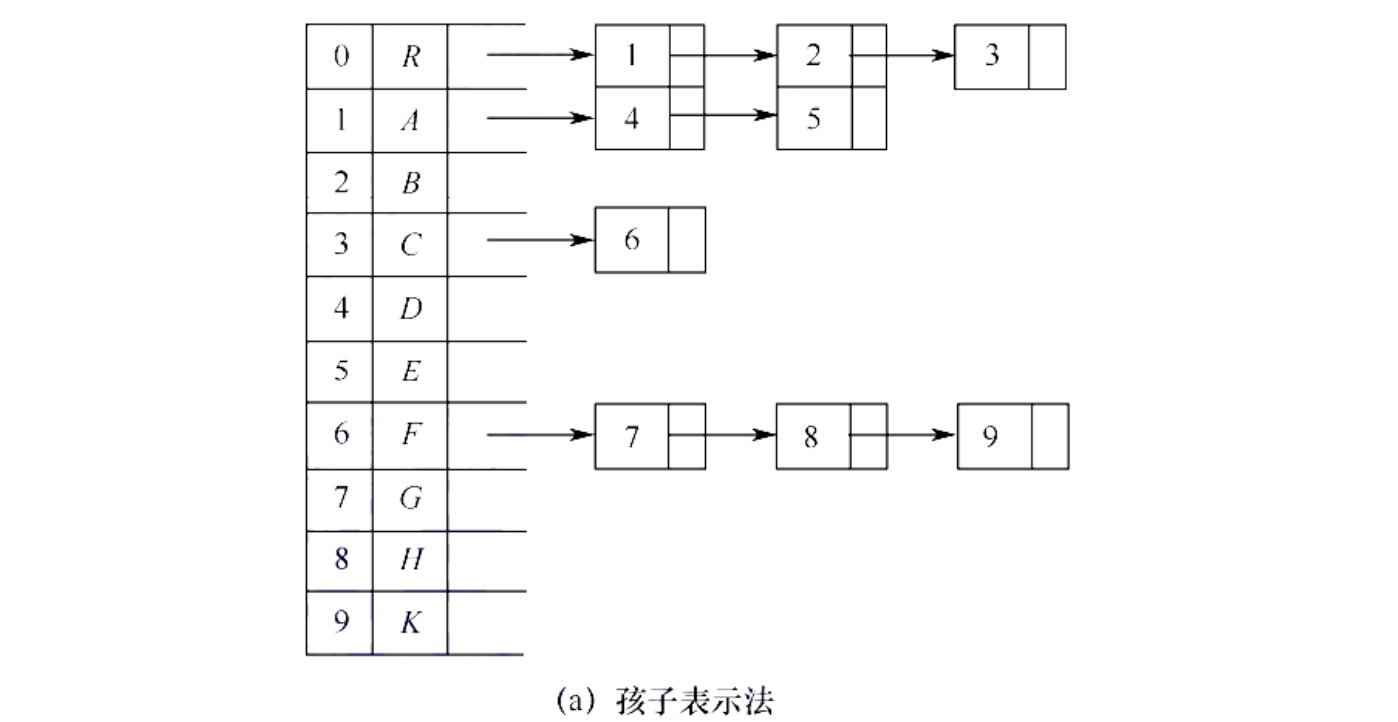
存储结构

// 孩子结点
typedef struct CTNode {
    int child;              // 孩子结点在数组中的位置
    struct CTNode *next;    // 指向下一个孩子结点
} *ChildPtr;
 
// 双亲结点
typedef struct {
    ElemType data;          // 结点数据
    ChildPtr firstchild;    // 指向第一个孩子的指针
} CTBox;
 
typedef struct {
    CTBox nodes[MAX_SIZE];  // 结点数组
    int n, r;              // 结点数和根的位置
} CTree;

特点分析

• 优点：寻找孩子的操作比较方便，查找某结点的第 k 个孩子的时间复杂度为 O(k)
• 缺点：寻找双亲需要遍历每个结点的孩子链表，时间复杂度为 O(n)
• 空间复杂度：O(n)，其中 n 为结点个数
• 适用场景：适合需要频繁访问孩子结点的应用

孩子兄弟表示法

基本思想

也称二叉树表示法或左孩子右兄弟表示法，用二叉链表作为树的存储结构。每个结点包含数据域和两个指针域：一个指向结点的第一个孩子，另一个指向结点的下一个兄弟。

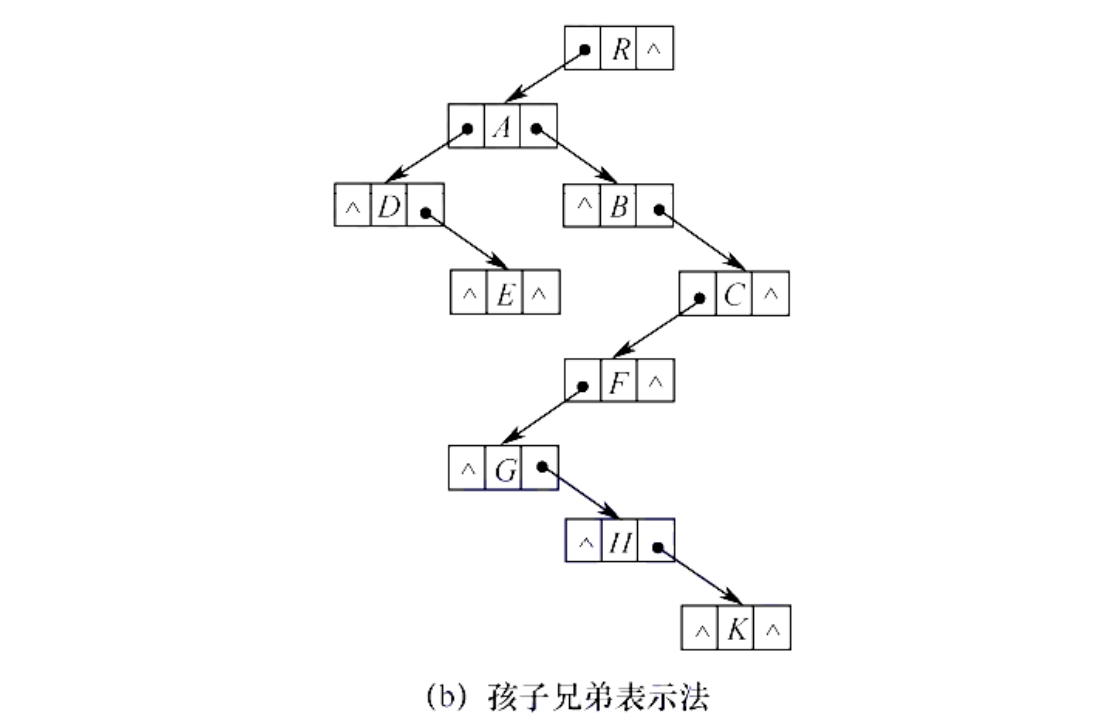
存储结构

typedef struct CSNode {
    ElemType data;              // 数据域
    struct CSNode *firstchild;  // 第一个孩子指针
    struct CSNode *nextsibling; // 下一个兄弟指针
} CSNode, *CSTree;

特点分析

• 优点：
  • 可以方便地实现树转换为二叉树的操作
  • 容易查找孩子结点
  • 存储结构简单，便于实现各种树的操作
• 缺点：从当前结点查找其双亲比较麻烦，需要从根结点开始遍历
• 时间复杂度：查找孩子 O(k)，查找双亲 O(n)

改进方案

三叉链表表示法：在孩子兄弟表示法的基础上，再增设一个双亲指针，形成三叉链表。

typedef struct CSNode {
    ElemType data;
    struct CSNode *firstchild;
    struct CSNode *nextsibling;
    struct CSNode *parent;      // 双亲指针
} CSNode, *CSTree;

改进后可以方便地查找双亲结点，但增加了存储开销。

存储方法比较

存储方法	查找双亲	查找孩子	存储空间	适用场景
双亲表示法	O(1)	O(n)	较小	频繁查找双亲
孩子表示法	O(n)	O(k)	较大	频繁查找孩子
孩子兄弟表示法	O(n)	O(k)	中等	一般树操作，树转二叉树
三叉链表	O(1)	O(k)	较大	双向查找频繁

注：k 为某结点的孩子个数，n 为树的结点总数。