树、森林的转换与遍历

基本对应关系

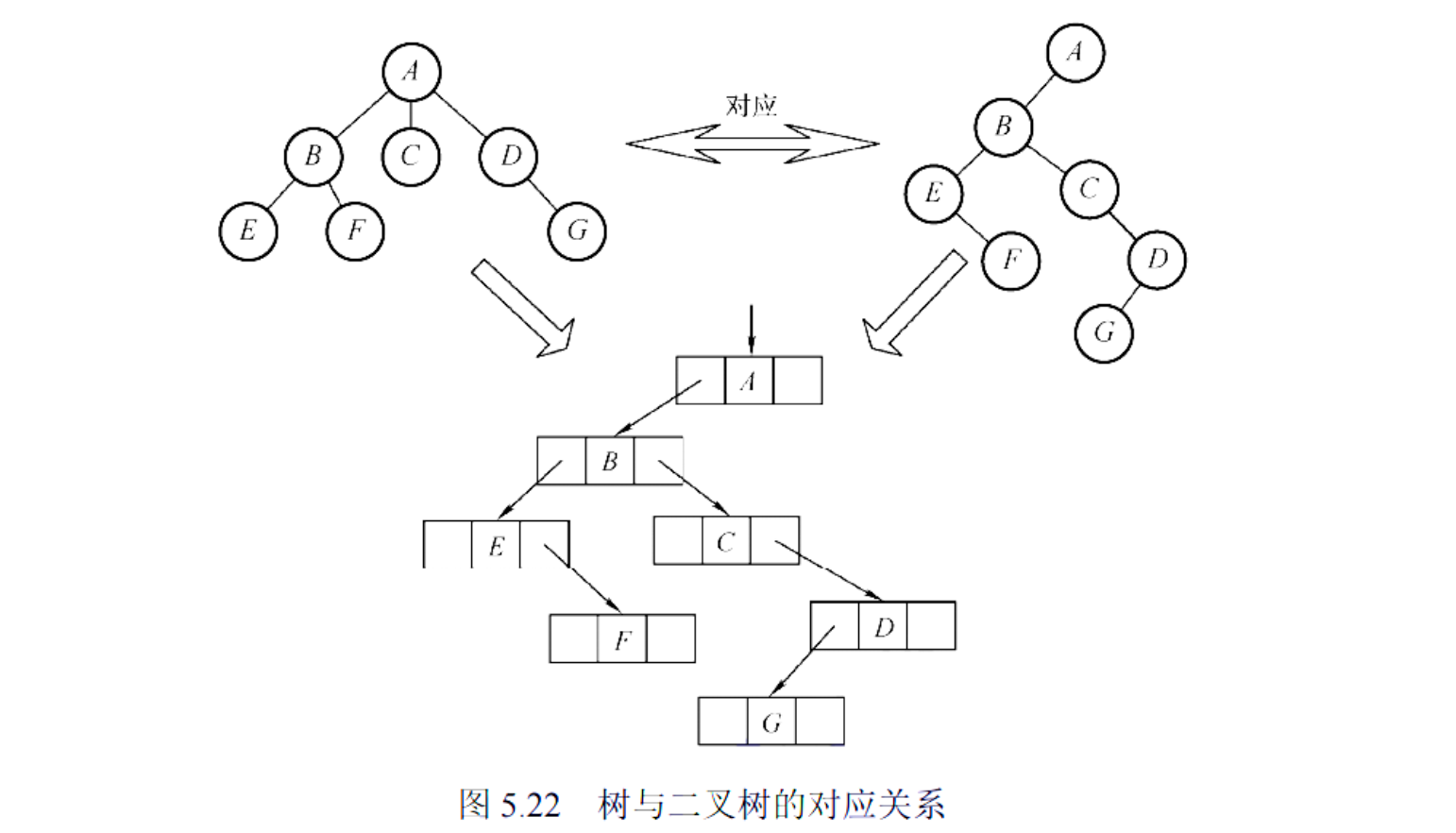
二叉树、一般树和森林之间存在一对一的结构对应关系，这种对应关系通过 ” 左子右兄 ” 转换规则实现。

树到二叉树的转换（左子右兄表示法）

转换规则：

左孩子指针：指向该结点的第一个孩子
右孩子指针：指向该结点的下一个兄弟

转换步骤：

连接所有兄弟结点（水平连线）
对每个结点，只保留其与第一个孩子的连线，删除与其他孩子的连线
顺时针旋转 45° 得到二叉树

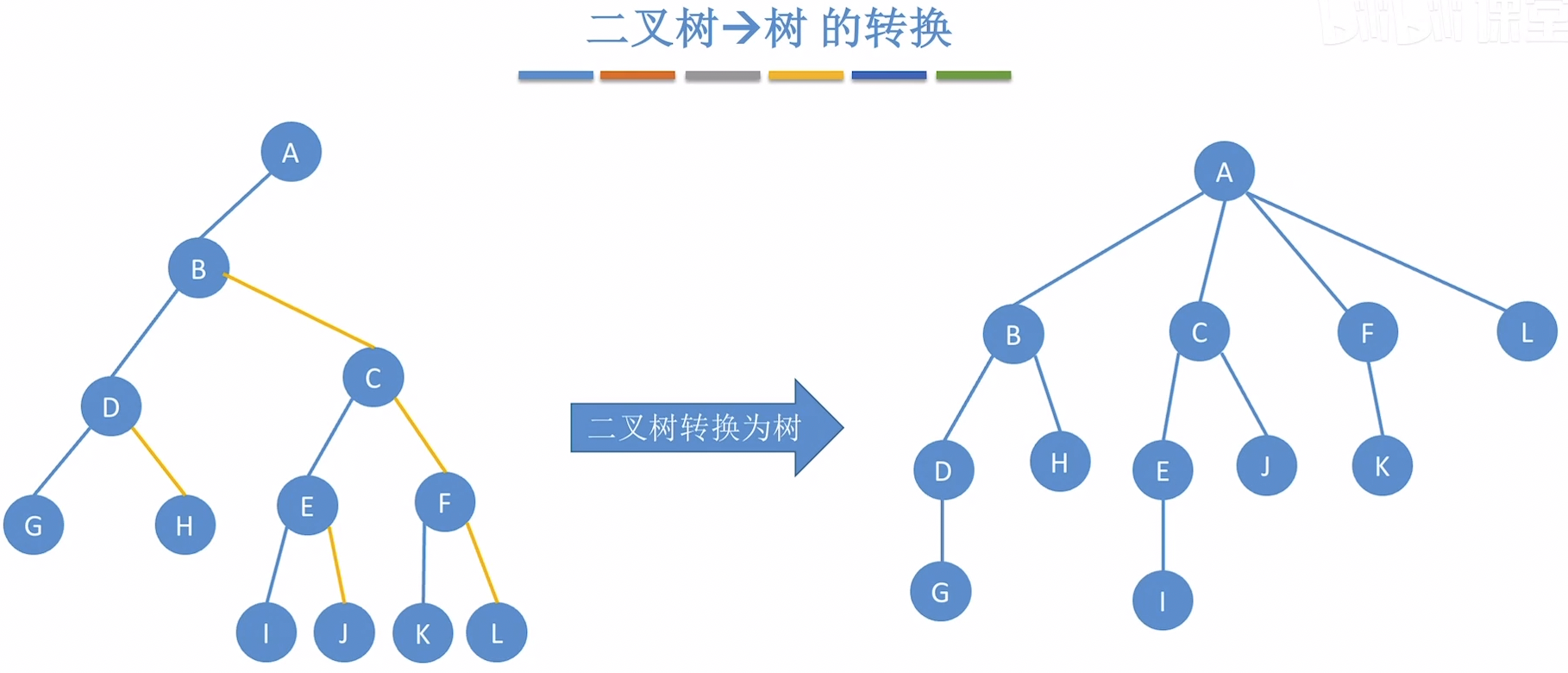
森林到二叉树的转换

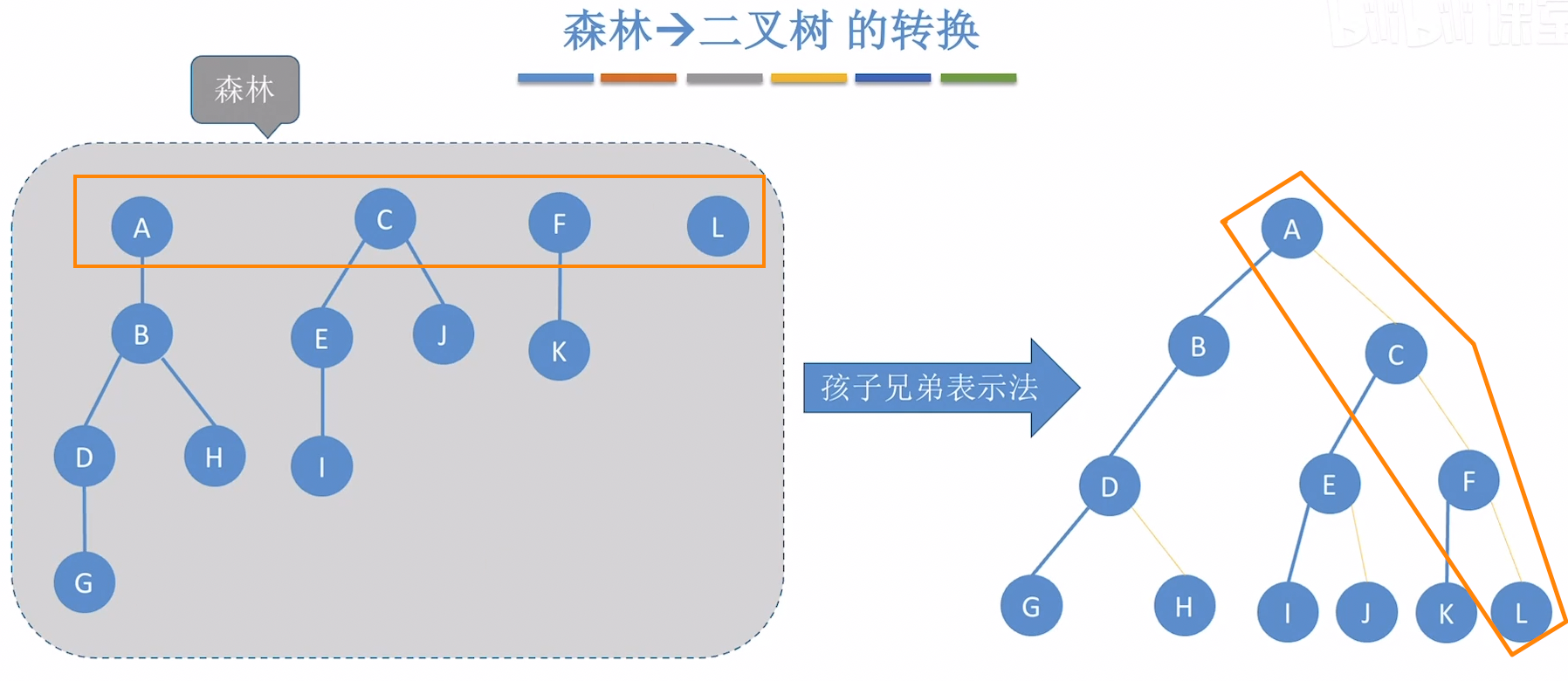
转换规则：

将森林中每棵树转换为二叉树
- 转换结果：经过上述步骤，每棵树都将转换为一棵二叉树，其中原树的父子关系转换为二叉树的左孩子关系，原树的兄弟关系转换为二叉树的右孩子关系。
各棵树的根结点通过 ” 兄弟关系 ” 连接（即第二棵树的根作为第一棵树根的右孩子）
- 具体步骤：将转换后的第一棵二叉树的根结点作为总二叉树的根结点。将第二棵二叉树的根结点连接到第一棵二叉树根结点的右孩子上，第三棵二叉树的根结点连接到第二棵二叉树根结点的右孩子上，以此类推，直到所有转换后的二叉树的根结点都被连接起来。

二叉树到森林的转换

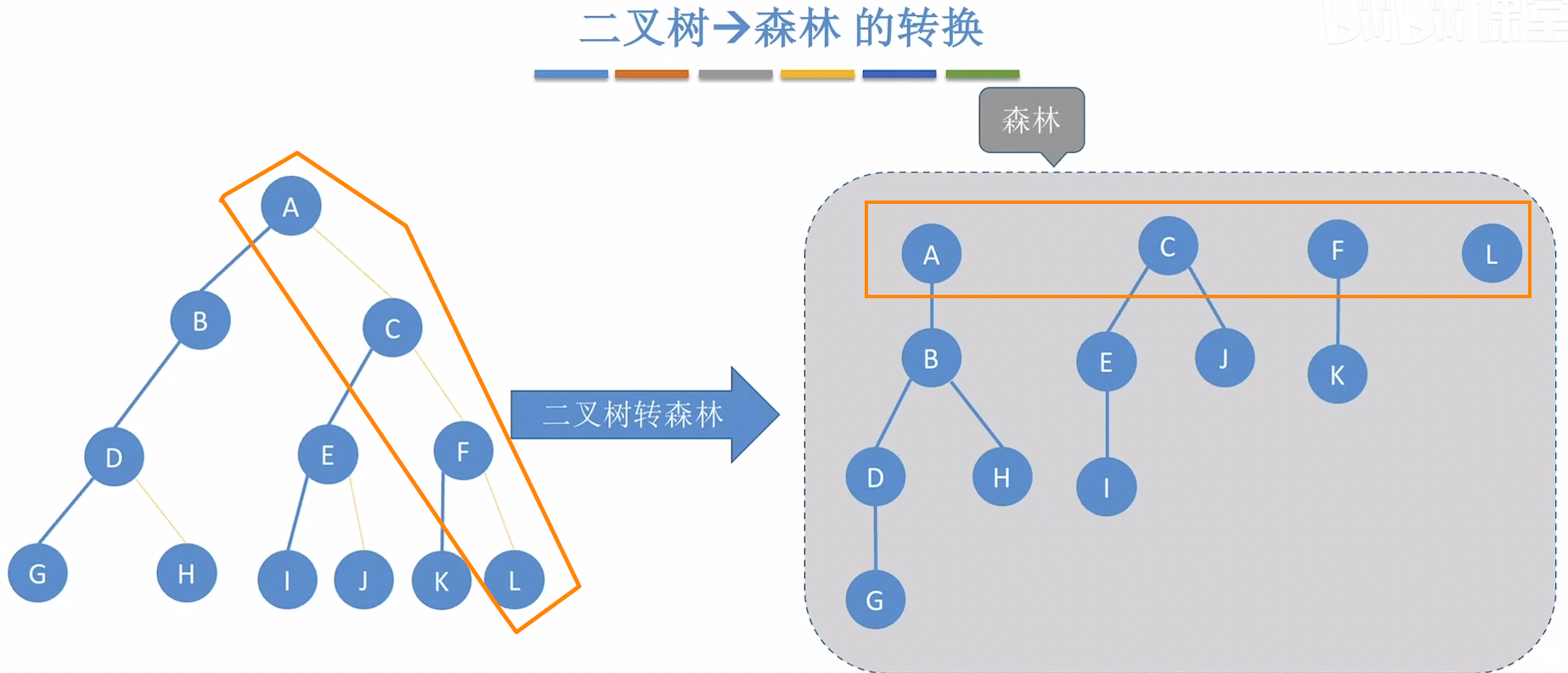
转换规则：

逆转右孩子关系：对于二叉树中的每个结点，如果它有右孩子，则将该右孩子视为其兄弟结点。
逆转左孩子关系：对于二叉树中的每个结点，如果它有左孩子，则将该左孩子视为其第一个孩子结点。
分离独立树：从二叉树的根结点开始，沿着右孩子链找到所有原森林中树的根结点。每个这样的根结点及其左孩子子树（以及这些左孩子的右孩子子树，即其兄弟）构成原森林中的一棵树。
- 具体步骤：
  1. 从二叉树的根结点开始，沿着左孩子链找到所有父子关系。
  2. 对于每个结点，其右孩子是其兄弟结点的根，解除父子关系并建立兄弟关系。
  3. 最终，二叉树的根结点及其所有右兄弟链上的结点（以及它们各自的左子树）将构成森林中的多棵树。
- 转换结果：将二叉树还原为多棵独立的树，每棵树都反映了原森林中对应树的结构。
- 特点：
  - 原二叉树中结点的左孩子是其在森林中的第一个孩子。
  - 原二叉树中结点的右孩子是其在森林中的下一个兄弟。

树和森林的遍历

树的遍历

先根遍历

定义：先访问树的根结点，然后依次先根遍历根的每棵子树。
顺序：根 $\to$ 子树 1（先根） $\to$ 子树 2（先根） $\to \dots$
与二叉树的关系：等同于将树转换为二叉树后的先序遍历。

后根遍历

定义：先依次后根遍历根的每棵子树，最后访问树的根结点。
顺序：子树 1（后根） $\to$ 子树 2（后根） $\to \dots \to$ 根
与二叉树的关系：等同于将树转换为二叉树后的中序遍历。

层次遍历

定义：从树的根结点开始，按层次逐层访问结点，同一层次的结点按从左到右的顺序访问。
顺序：根 $\to$ 第一层所有结点（从左到右） $\to$ 第二层所有结点（从左到右） $\to \dots$
实现：通常使用队列来实现。

森林的遍历

先序遍历森林

定义：
1. 访问森林中第一棵树的根结点。
2. 先序遍历第一棵树的子树森林。
3. 先序遍历除去第一棵树的剩余森林。
与二叉树的关系：等同于将森林转换为二叉树后的先序遍历。

中序遍历森林

定义：
1. 中序遍历森林中第一棵树的子树森林。
2. 访问森林中第一棵树的根结点。
3. 中序遍历除去第一棵树的剩余森林。
与二叉树的关系：等同于将森林转换为二叉树后的中序遍历。

树、森林、二叉树遍历顺序的对应关系

结构	遍历方式	对应二叉树遍历方式
树	先根遍历	先序遍历
	后根遍历	中序遍历
	层次遍历	无直接对应，但可类比二叉树的层次遍历
森林	先序遍历	先序遍历
	中序遍历	中序遍历