11 函数
函数概念及常见函数
函数概念
定义: 设 、 是两个非空数集,如果按照某个确定的对应关系 ,使对于集合 中的任意一个数 ,在集合 中都有唯一确定的数 与之对应,则称 为从 到 的函数,记作 , 。
要素:
- 定义域:
- 值域:
- 对应关系:
函数相等条件: 定义域相同且对应关系相同
复合函数
定义: 设函数 的定义域为 ,函数 的定义域为 ,值域为 。若 ,则称函数 为 与 的复合函数。
复合函数存在条件: 内函数的值域与外函数的定义域有交集
定义域:
反函数
定义: 设函数 ,,值域为 。如果对于 中任意一个 ,在 中都有唯一的 使得 ,则称函数 , 为 的反函数。
存在条件: 函数 在其定义域上单调 (有唯一的 使得 )
性质:
- ,
- ,
- 与 的图形关于直线 对称
初等函数
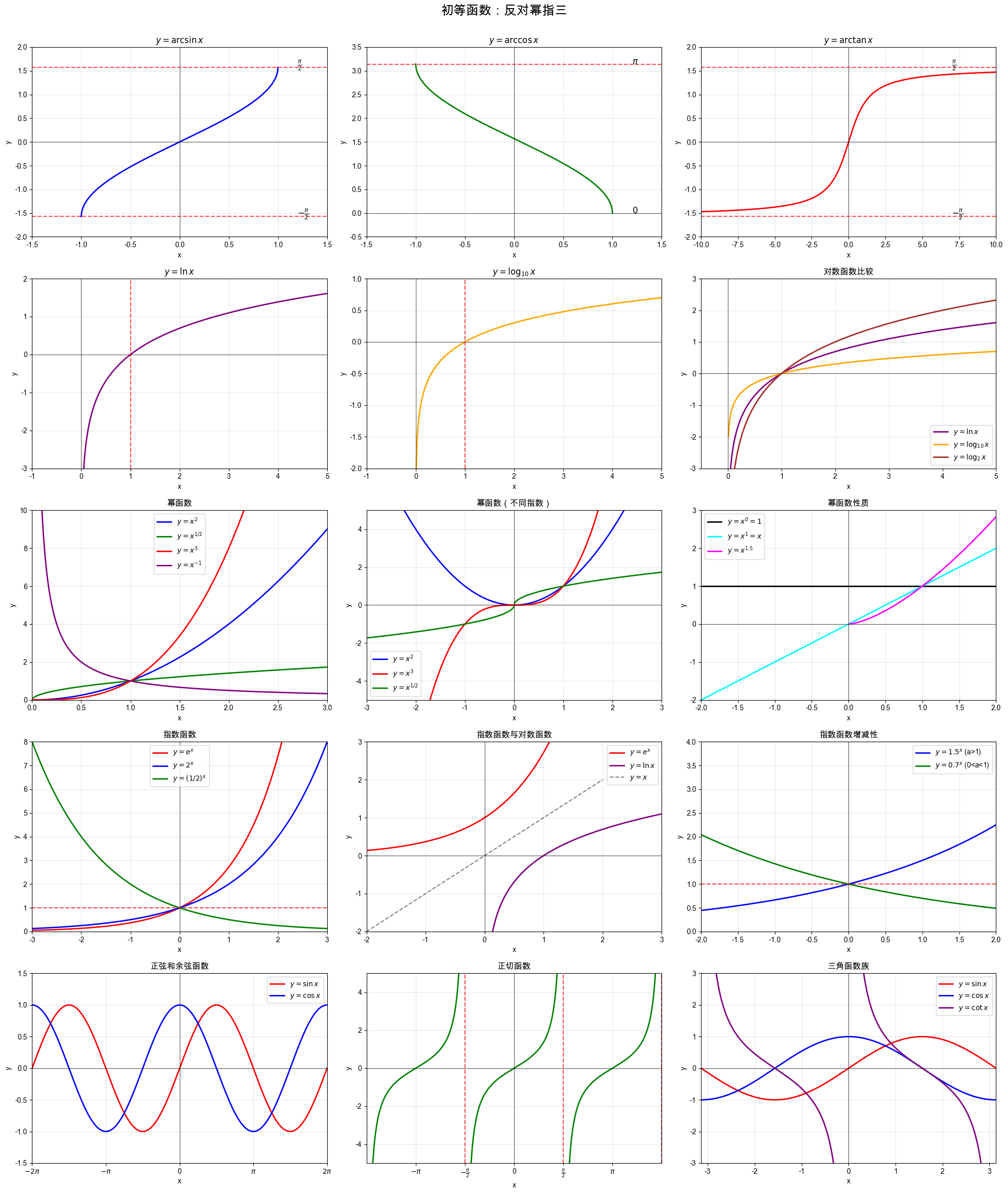
反对幂指三
- 反三角函数: , , , 等
- 对数函数: (其中 , ),特别地
- 幂函数: (其中 为实常数)
- 指数函数: (其中 , ),特别地
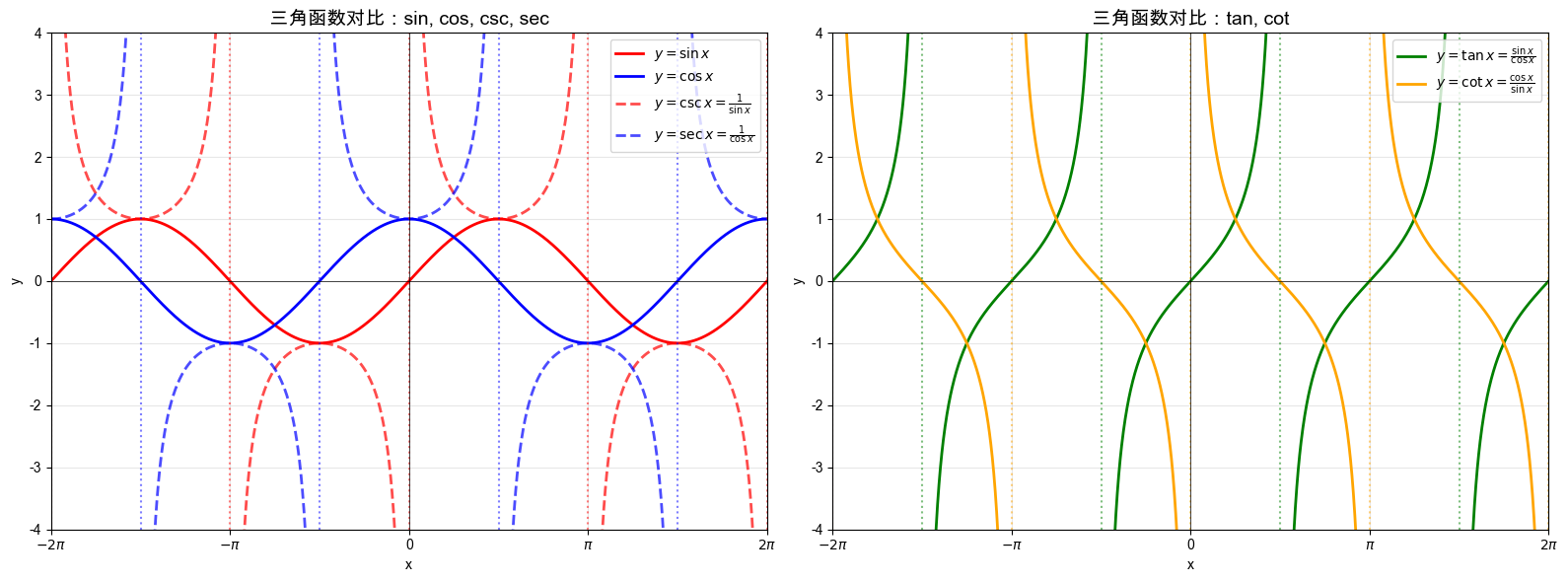
- 三角函数: , , , , ,
初等函数: 由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数。
| 函数类型 | 定义域 | 值域 | 单调性 | 奇偶性 | 周期 | 特殊值 |
|---|---|---|---|---|---|---|
| 反正弦 arcsin x | [-1, 1] | [-π/2, π/2] | ↗ | 奇 | 无 | arcsin 0 = 0 |
| 反余弦 arccos x | [-1, 1] | [0, π] | ↘ | 非奇非偶 | 无 | arccos 1 = 0 |
| 反正切 arctan x | (-∞, +∞) | (-π/2, π/2) | ↗ | 奇 | 无 | arctan 0 = 0 |
| 自然对数 ln x | (0, +∞) | (-∞, +∞) | ↗ | 非奇非偶 | 无 | ln 1 = 0 |
| 指数函数 e^x | (-∞, +∞) | (0, +∞) | ↗ | 非奇非偶 | 无 | e^0 = 1 |
| 正弦 sin x | (-∞, +∞) | [-1, 1] | 周期性 | 奇 | 2π | sin 0 = 0 |
| 余弦 cos x | (-∞, +∞) | [-1, 1] | 周期性 | 偶 | 2π | cos 0 = 1 |
| 正切 tan x | x ≠ kπ + π/2, k∈Z | (-∞, +∞) | 周期性 | 奇 | π | tan 0 = 0 |
函数性态
单调性
判定:
- 定义: 设函数 在区间 上有定义,若对任意 ,当 时,恒有 (或 ),则称 在 上单调递增(或单调递减)。
- 导函数不小于 → 原函数单调不减: 若 在 上连续,在 内可导,且 (或 ),则 在 上单调递增(或单调递减)。
注意: 若 (或 ),则 严格单调递增(或严格单调递减)。
奇偶性
判定:
-
定义: 设函数 的定义域 关于原点对称,若对任意 :
- 偶函数:
- 奇函数:
-
函数的导数:
- 若 为偶函数,则 为奇函数
- 若 为奇函数,则 为偶函数
-
连续函数的原函数:
- 若 为偶函数,则其原函数中必存在奇函数
- 若 为奇函数,则其任一原函数都是偶函数
复合函数奇偶性
设复合函数为 ,其定义域为 。判断其奇偶性的前提是定义域 必须关于原点对称。若定义域不对称,则函数为非奇非偶函数。
判定步骤:
- 求定义域: 首先确定复合函数 的定义域 ,并判断 是否关于原点对称。
- 应用法则: 在定义域对称的前提下,根据内外层函数的奇偶性进行判断。
判定法则(“内偶则偶,内奇同外”)
设函数 和 的奇偶性已知。
-
内函数 为偶函数:
- 无论外函数 是奇函数、偶函数,还是非奇非偶函数,复合函数 必为偶函数。
- 推导: , 。
-
内函数 为奇函数:
- 复合函数 的奇偶性与外函数 的奇偶性相同。
- 若 为偶函数,则 为偶函数。
- 推导: 。
- 若 为奇函数,则 为奇函数。
- 推导: 。
总结表
| 外函数 | 内函数 | 复合函数 | 记忆口诀 |
|---|---|---|---|
| 任意函数 | 偶函数 | 偶函数 | 内偶则偶 |
| 偶函数 | 奇函数 | 偶函数 | 内奇同外 |
| 奇函数 | 奇函数 | 奇函数 | 内奇同外 |
注意事项:
- 定义域优先: 必须首先检验复合函数的定义域是否关于原点对称。例如,,内函数 为偶函数,外函数 的定义域为 。复合函数定义域为 ,关于原点对称,因此 是偶函数。
- 特殊情况: 如果内函数或外函数为非奇非偶函数(且不满足“内偶则偶”的情况),则必须回到奇偶性的定义,即计算 ,并观察其与 的关系来判断。
泰勒展开的性质
- 偶函数的泰勒展开只含偶次项: 若 为偶函数,则其麦克劳林级数展开为
- 奇函数的泰勒展开只含奇次项: 若 为奇函数,则其麦克劳林级数展开为
证明思路: 由于 (偶函数),将麦克劳林展开式中的 替换为 ,比较系数可得奇次项系数为零。
几何意义
- 奇函数关于原点对称,且若 x=0 有定义则 f(0)=0
- 偶函数图形关于 y 轴对称
周期性
判定:
- 定义: 设函数 在数集 上有定义,若存在正常数 ,使得对任意 有 且 ,则称 为周期函数, 为 的一个周期。最小正周期是所有正周期中的最小者。
- 可导的周期函数,其导函数为周期函数: 若 是周期为 的可导函数,则 也是周期为 的函数。
- 周期函数的原函数不一定为周期函数: 例如 ,其原函数 不是周期函数。
周期性充要条件:
(1) 设 连续且以 为周期,则
(2) 周期函数的原函数是周期函数的充要条件是其在一个周期上的积分为零。
说明:
- 当 时,原函数 会有线性增长趋势,不可能是周期函数
- 当 时,原函数 在每个周期内的增量为零,因此保持周期性
有界性
判定:
- 定义: 设函数 在数集 上有定义,若存在正数 ,使得对任意 都有 ,则称 在 上有界。
- 利用闭区间连续: 若 在闭区间 上连续,则 在 上有界(有界性定理)。
- 利用开区间连续 + 区间内侧极限存在: 若 在开区间 内连续,且 和 都存在,则 在 内有界。
- 导函数在有限区间上有界⇒原函数在该区间上有界: 若 在有限区间 上有界,即存在 使得 ,则由拉格朗日中值定理可知 在 上有界。