逻辑移位和算数移位
计算机中数字的表示方式(原码、反码、补码)会影响其移位操作的行为。以下是对原码、反码、补码的逻辑移位和算术移位知识点的归纳 。
逻辑移位 (Logical Shift)
逻辑移位不考虑符号位,将操作数视为无符号数进行移位 。
- 逻辑左移 (Logical Left Shift): 所有位向左移动,高位(最左边位)移出并丢弃,低位(最右边位)补 0 。
- 逻辑右移 (Logical Right Shift): 所有位向右移动,低位(最右边位)移出并丢弃,高位(最左边位)补 0 。
逻辑移位可以看作是对“无符号数”的算术移位 。
算术移位 (Arithmetic Shift)
算术移位会考虑符号位,用于对有符号数进行乘以或除以 2 的幂次方的操作 。
1. 原码 (Sign-Magnitude) 的算术移位
原码的最高位是符号位(0 为正,1 为负),其余位表示数值的绝对值 。其算术移位规则是符号位保持不变,仅对数值位进行移位 。
- 正数和负数:
- 右移: 符号位不变,数值位向右移动。数值位的高位补 0,低位舍弃。若舍弃的位为 0,则近似于除以 2;若舍弃的位不为 0,则会丢失精度 。
- 左移: 符号位不变,数值位向左移动。数值位的低位补 0,高位舍弃。若舍弃的数值位为 0,则近似于乘以 2;若舍弃的数值位不为 0,则会产生严重误差,导致结果不正确 。
2. 反码 (One’s Complement) 的算术移位
正数的反码与其原码相同;负数的反码是其原码除符号位外,各位取反 。
- 正数:
- 反码与原码相同,因此其算术移位规则也与原码正数的算术移位相同(右移高位补 0,左移低位补 0)。
- 负数:
- 右移: 符号位为 1 保持不变。由于数值部分与原码相反,移位时高位(符号位之后的第一位)补 1,低位舍弃 。
- 左移: 符号位为 1 保持不变。数值部分的低位补 1,高位舍弃 。
3. 补码 (Two’s Complement) 的算术移位
正数的补码与其原码、反码相同;负数的补码是其反码加 1 。计算机内部通常使用补码进行运算 。
- 正数:
- 补码与原码相同,因此其算术移位规则也与原码正数的算术移位相同 。
- 右移: 高位补 0,低位舍弃 。
- 左移: 低位补 0,高位舍弃 。
- 负数:
- 右移: 符号位(最高位)为 1。为了保持数的符号和算术意义(除以 2 的效果),高位补 1(即复制符号位),低位舍弃 。
- 左移: 低位补 0,高位(包括符号位,如果发生溢出)舍弃 。左移一位相当于乘以 2,只要不发生溢出(即丢弃的位与新的符号位不同)。
总结算术移位规则
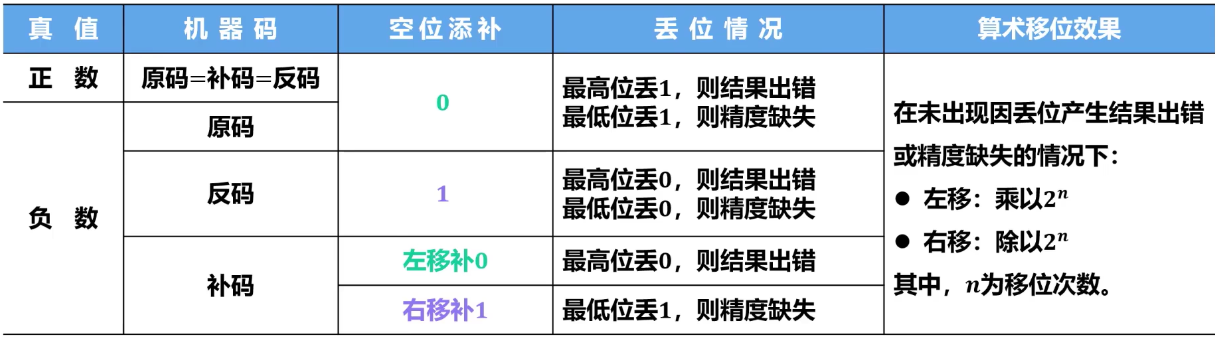
- 正数: 对于原码、反码、补码,正数的算术移位规则是相同的:右移时高位补 0,左移时低位补 0 。
- 负数:
- 原码: 符号位不变,数值位右移补 0,左移补 0 。
- 反码: 符号位不变,数值位右移补 1,左移补 1 。
- 补码: 右移时高位(符号位)补 1,左移时低位补 0 。