B 树
因为考点很多,无法全部提前推导。最好熟记基本性质,如每层关键字至多至少情况。根据问题需要进行推导。
区分关键字和结点
定义及特点
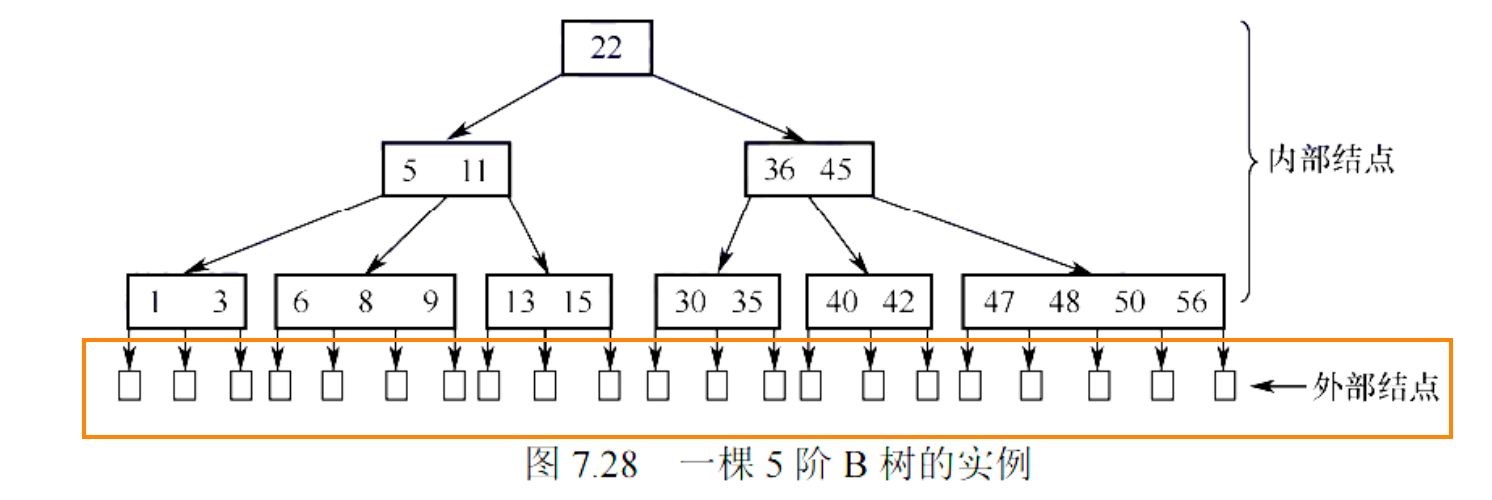
B 树 (B-Tree),又称多路平衡查找树,是一种为磁盘等外部存储设备设计的数据结构。它通过保持树的平衡来最小化磁盘 I/O 操作。一个 m 阶 B 树具有以下特点:
-
结点结构:每个内部结点由 组成。
- 为结点的关键字,且 。
- 为指向子树的指针。 指向的子树中所有关键字都小于 , 指向的子树中所有关键字都大于 。
- 为结点中关键字的个数。
-
关键字与子女数:
| 结点类型 | 关键字个数 (n) | 子女数 (分支、指针数) |
|---|---|---|
| 根结点 | (若非叶子) | |
| 非根内部结点 | ||
| 叶子结点 | 0 (不包含指向真实数据的指针) |
- 平衡性:所有的叶子结点都出现在同一层,并且不带信息(可以看作是查找失败的外部结点,指针为 NULL)。
| 特点 | 说明 |
|---|---|
| 多路性 | 每个结点最多有 棵子树, 称为 B 树的阶。 |
| 关键字有序 | 每个结点内的关键字递增排列。 |
| 关键字分布 | 结点中每个关键字将其子树分成区间,左小右大,便于查找。 |
| 结点容量限制 | 除根结点外,所有结点包含的关键字数在 之间 |
| 根特例 | 根结点最少包含 1 个关键字。 |
| 叶结点层次 | 所有叶结点位于同一层,树高较低。 |
| 动态平衡 | 插入、删除后可自动保持平衡。 |
- 支持随机查找,不支持顺序查找。(真题)
查找
B 树的查找是一个从根结点开始,自顶向下的多路比较过程:
- 从根结点开始,在当前结点的关键字序列中查找目标值(可使用顺序查找或二分查找)。
- 若找到,则查找成功。
- 若未找到,则判断目标值应属于哪个子树范围,然后沿着对应的指针 进入下一层子结点。
- 重复上述过程,直到找到关键字或查找到达叶子结点仍未找到(此时沿着 NULL 指针查找),则查找失败。
B 树的计算
B 树相关计算结论汇总:
| 参数类别 | 描述 | 最小情况 (对应高树/稀疏) | 最大情况 (对应矮树/稠密) | 备注 |
|---|---|---|---|---|
| 高度 | 影响查找、插入、删除操作的性能 | |||
| 关键字数 | 给定 时: | 给定 时: | 实际存储的数据量 | |
| 结点数 | 给定 时: | 给定 时: | 树的结构大小,影响内存占用和 IO 次数的估算 |
高度最大值
B 树的高度非常低,这是其高效的原因。对于包含 个关键字的 阶 B 树,其高度 (根为第 1 层) 的最大值为:
推导思路:
- 要使树高最大,则每个结点的关键字数量应尽可能少,即每个结点拥有的孩子数尽可能少。
- B 树的性质规定:
- 根结点至少有 2 个孩子。
- 除根结点外的所有非叶结点至少有 个孩子。
- 设树高为 ,则:
- 第 1 层 (根):1 个结点,至少有 2 个孩子。
- 第 2 层:至少有 2 个结点 (由根结点的孩子构成)。
- 第 3 层:至少有 个结点 (由第 2 层每个结点至少 个孩子构成)。
- 第 层 ():至少有 个结点。
- 最底层(叶子结点层,也可以理解为指向外部结点的指针层)的指针总数等于 B 树中关键字总数 加 1,即 。
- 为了使树高最大,所有非叶结点都应取最小孩子数。因此,最底层叶子指针的总数 至少为:
- 通过此不等式可推导出高度上限:
高度最小值
对于包含 个关键字的 阶 B 树,其高度 (根为第 1 层) 的最小值为:
推导思路:
- 要使树高最小,则每个结点的关键字数量应尽可能多,即每个结点拥有的孩子数尽可能多。
- B 树的性质规定:
- 所有非叶结点最多有 个孩子。
- 每个结点最多有 个关键字。
- 设树高为 ,则:
- 第 1 层 (根):1 个结点,最多有 个孩子。
- 第 2 层:最多有 个结点。
- 第 3 层:最多有 个结点。
- 第 层:最多有 个结点。
- 树中总关键字数 满足:
- 每个结点最多有 个关键字。
- 这是一个等比数列求和:
- 通过此不等式可推导出高度下限:
- 由于树高 必须为整数,因此最小高度 。
插入
插入操作总是发生在叶子结点层。
- 定位:利用查找算法找到要插入关键字的最低层叶子结点。
- 插入:
- 若该叶子结点中的关键字个数 ,直接将新关键字插入到该结点中,保持关键字有序。
- 若该叶子结点中的关键字个数 ,插入后导致结点溢出 (Overflow)。
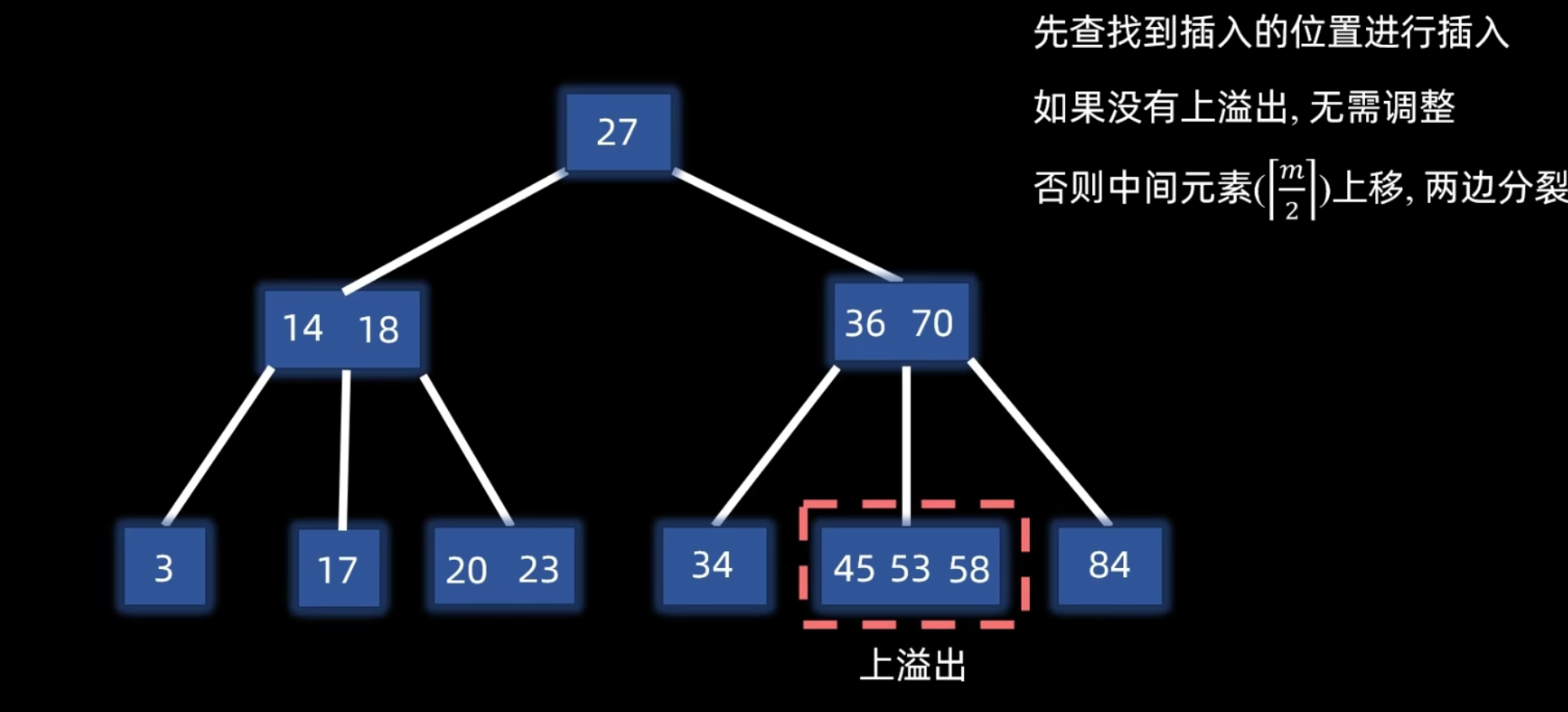
- 分裂:处理溢出结点。
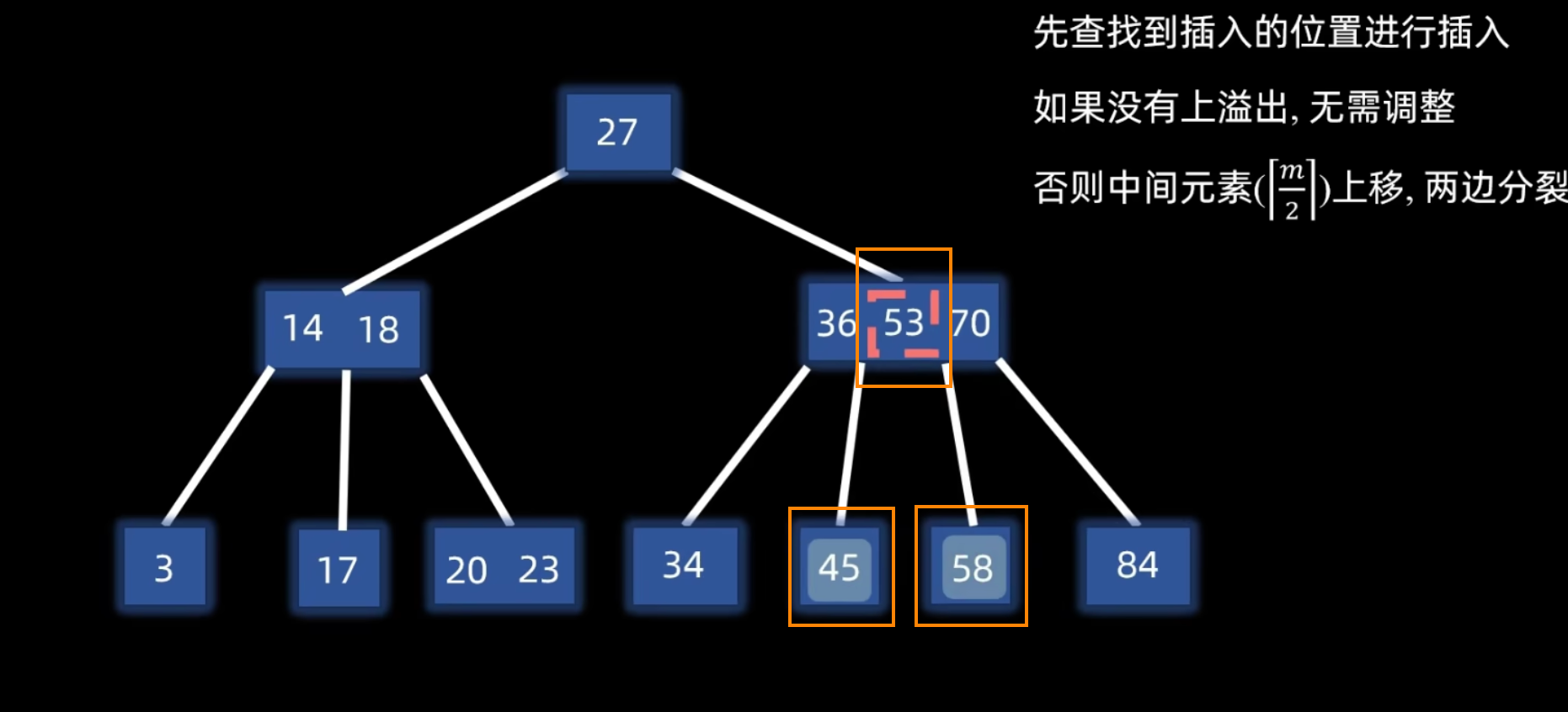
- 将该结点(包含新插入的关键字,共 个)从中间位置 分裂成两个新结点(分裂完成后变为左、中、右三个部分)。
- 将中间位置的关键字提升 (Promote) 到其父结点中。
- 原结点的左半部分关键字留在原结点,右半部分关键字放入一个新创建的结点。
- 递归分裂:如果因关键字提升导致父结点也溢出,则对父结点重复分裂操作,直到不再溢出或分裂到根结点。若根结点分裂,则树的高度增加 1。
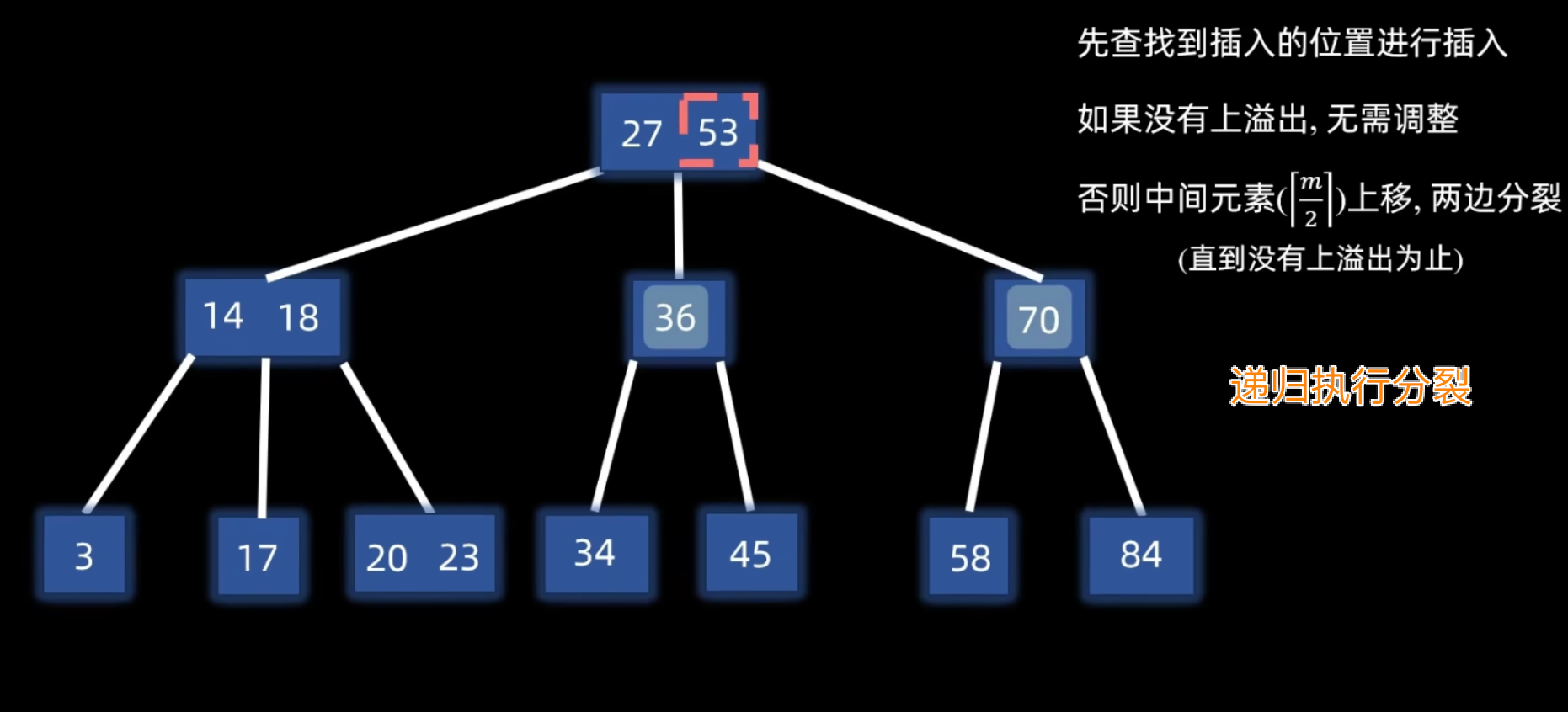
另一个例子:根结点上溢出
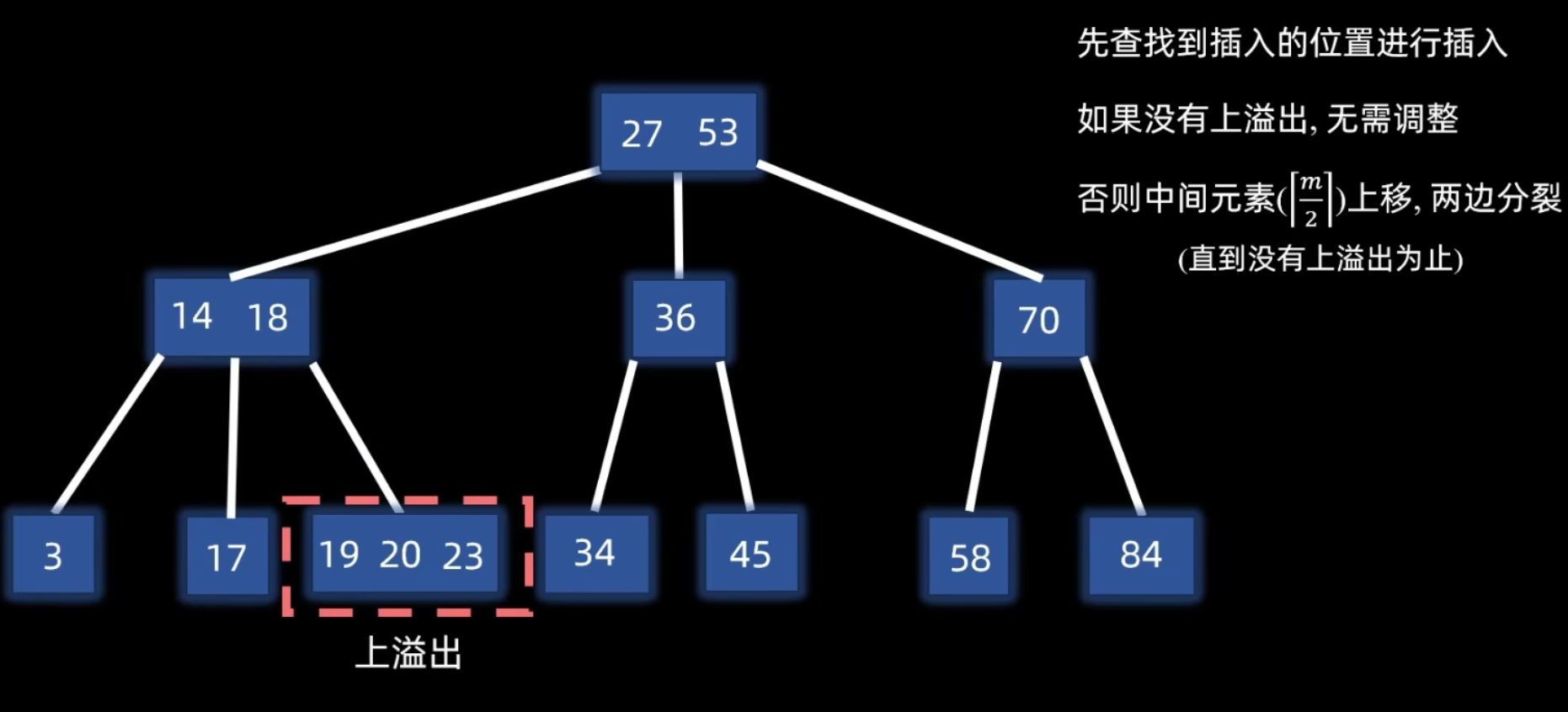
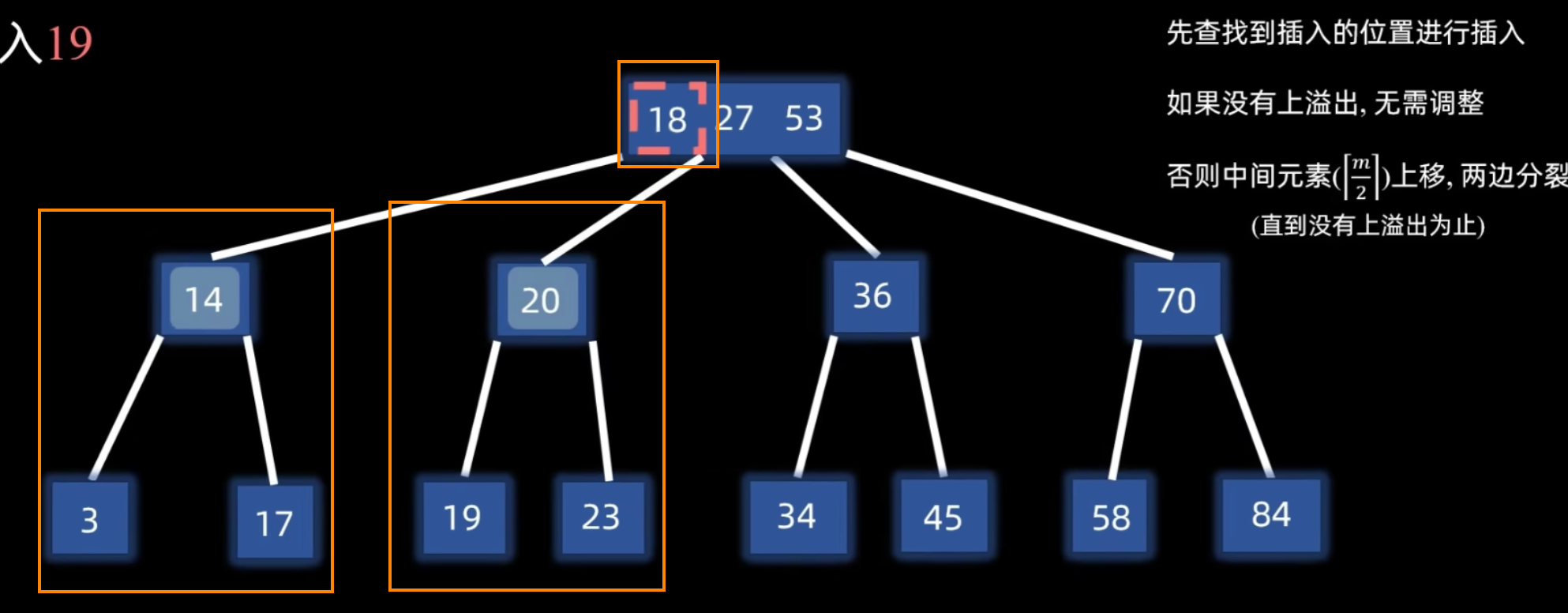
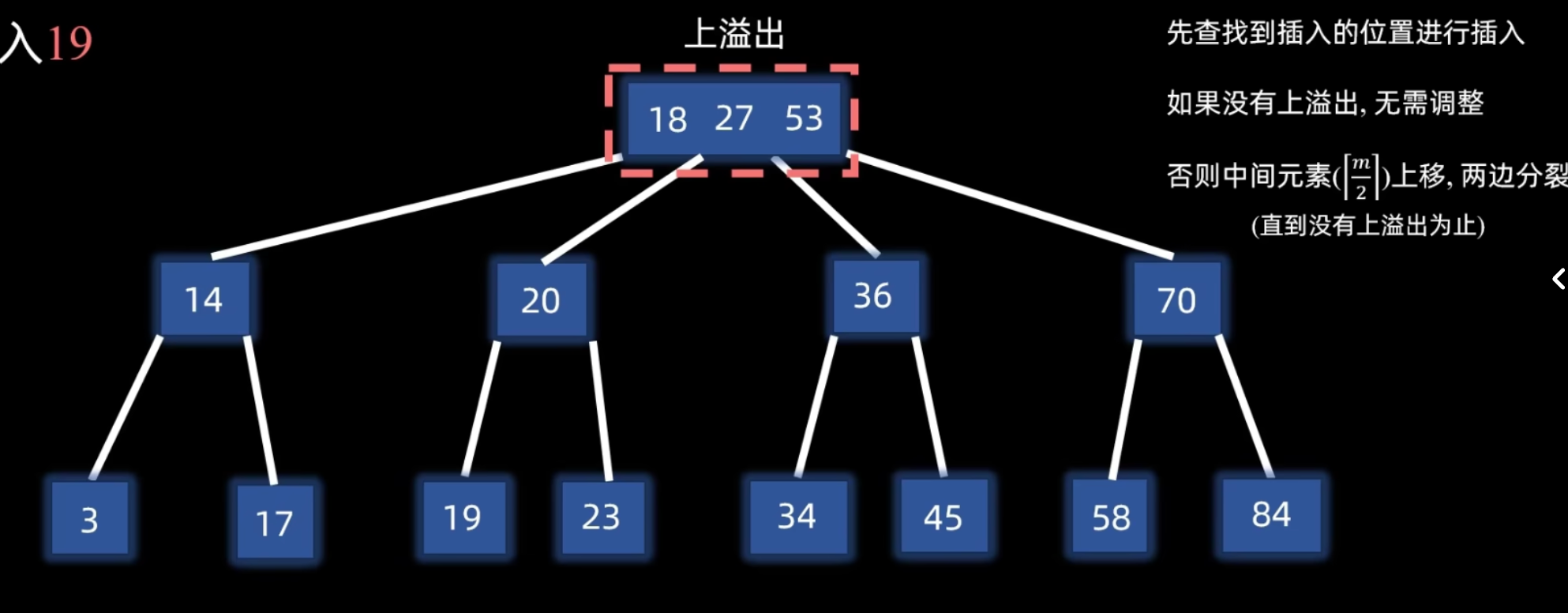
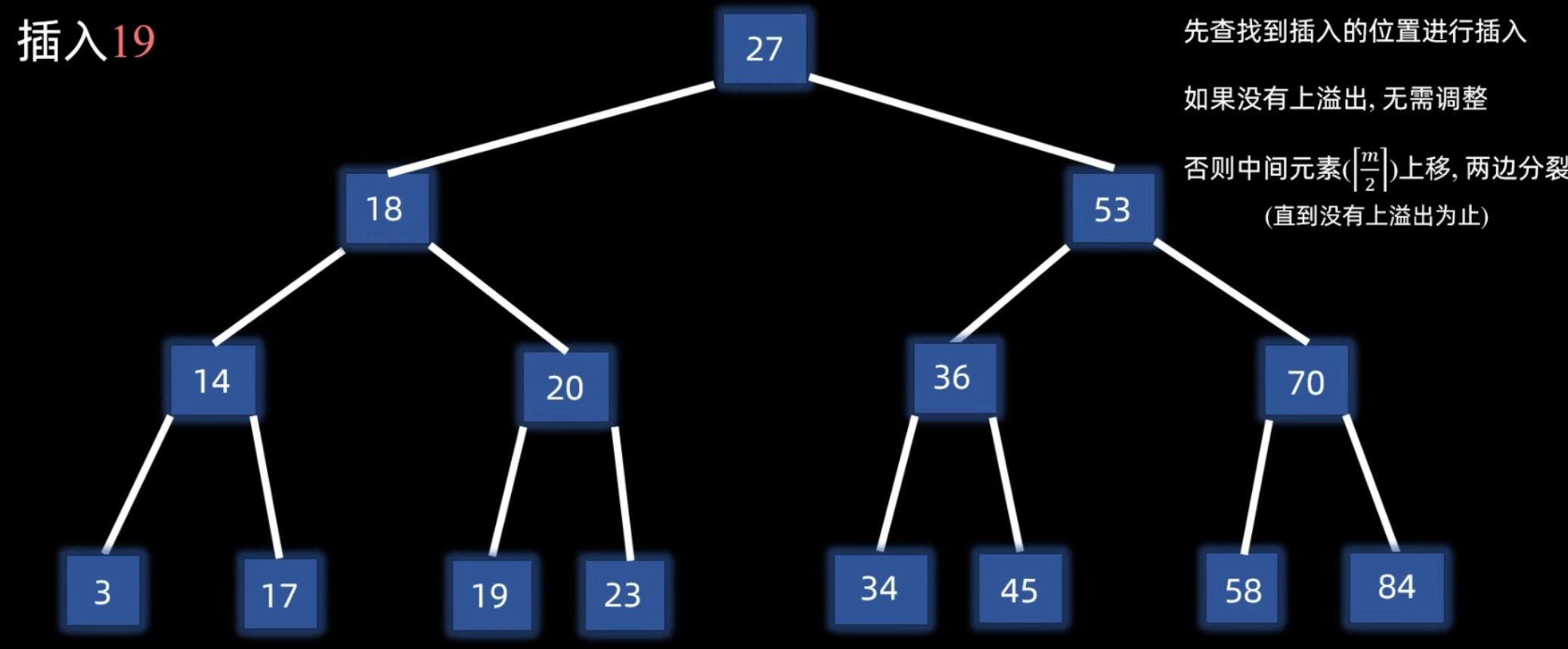
B 树构建

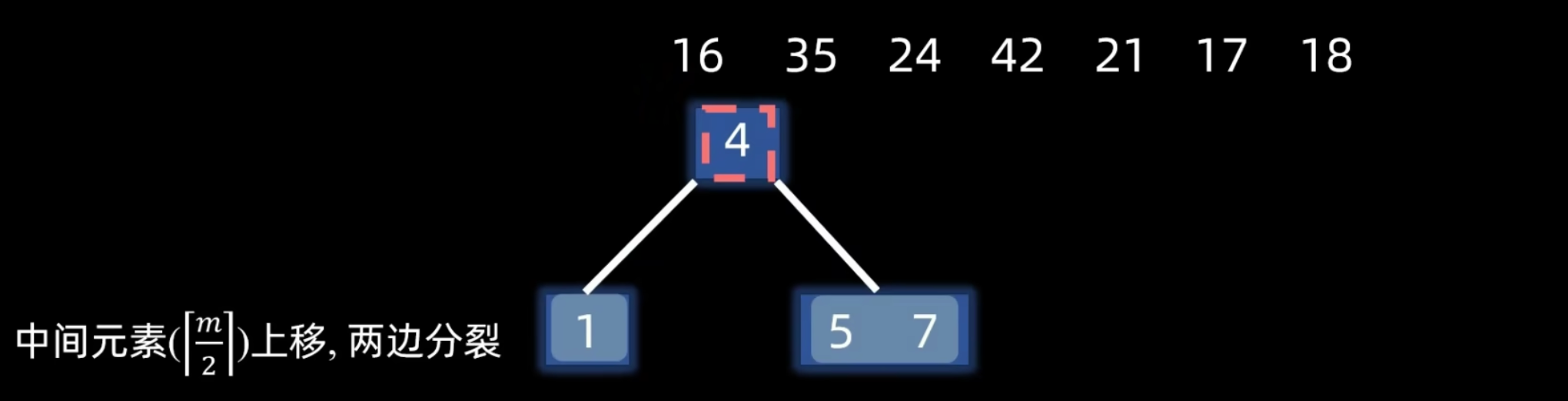
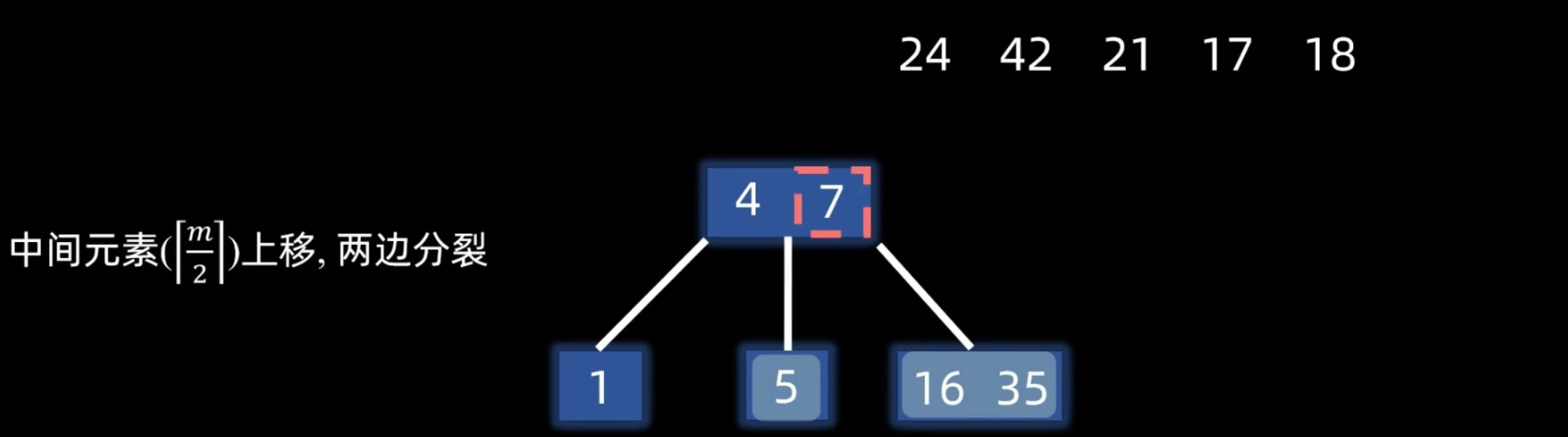
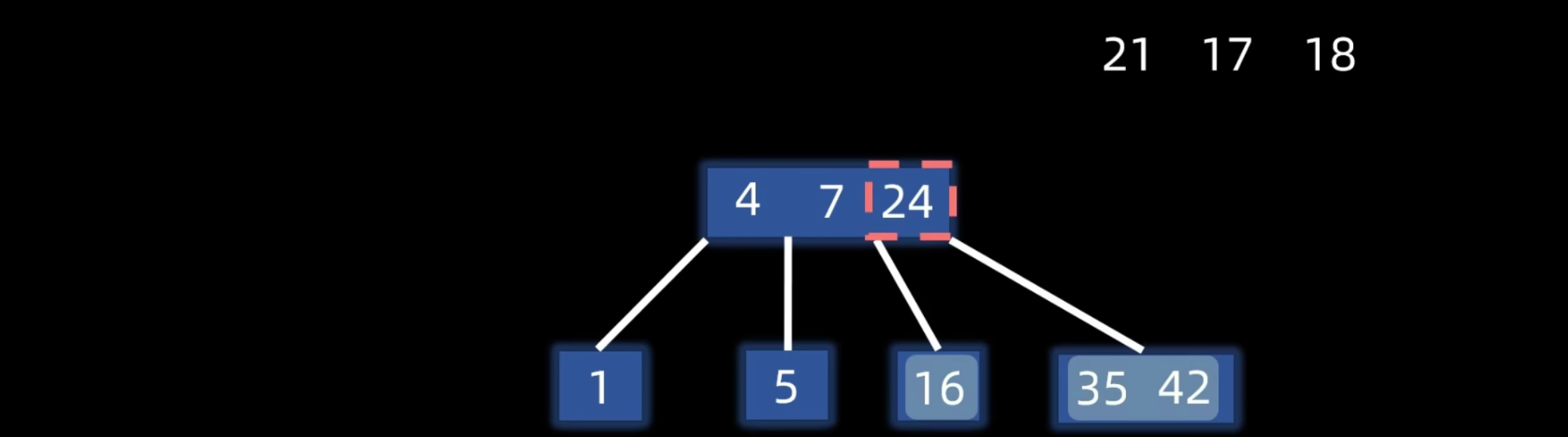

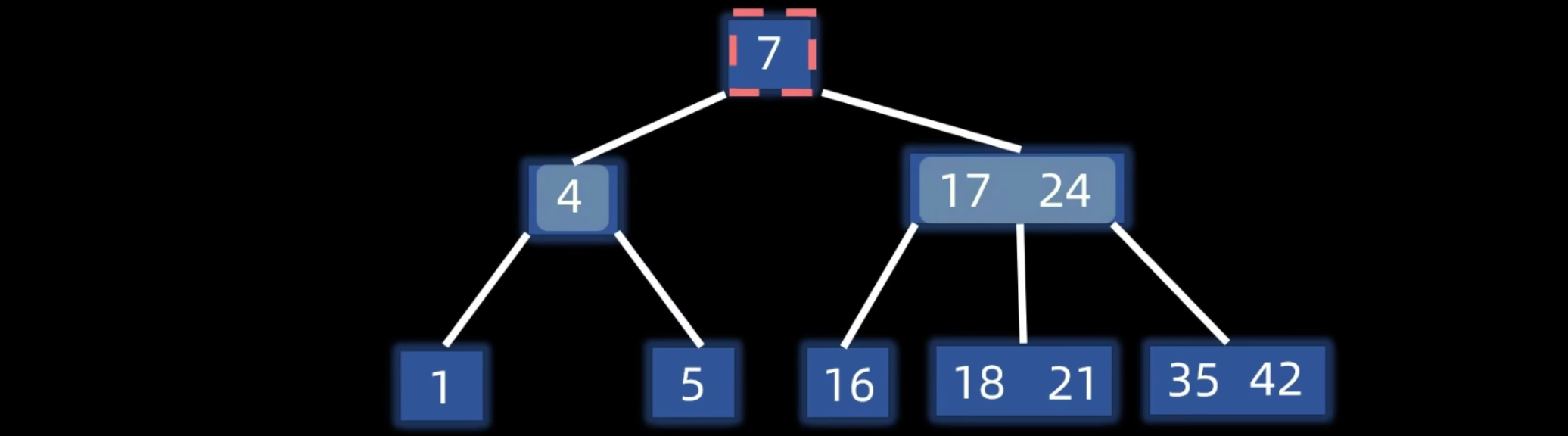
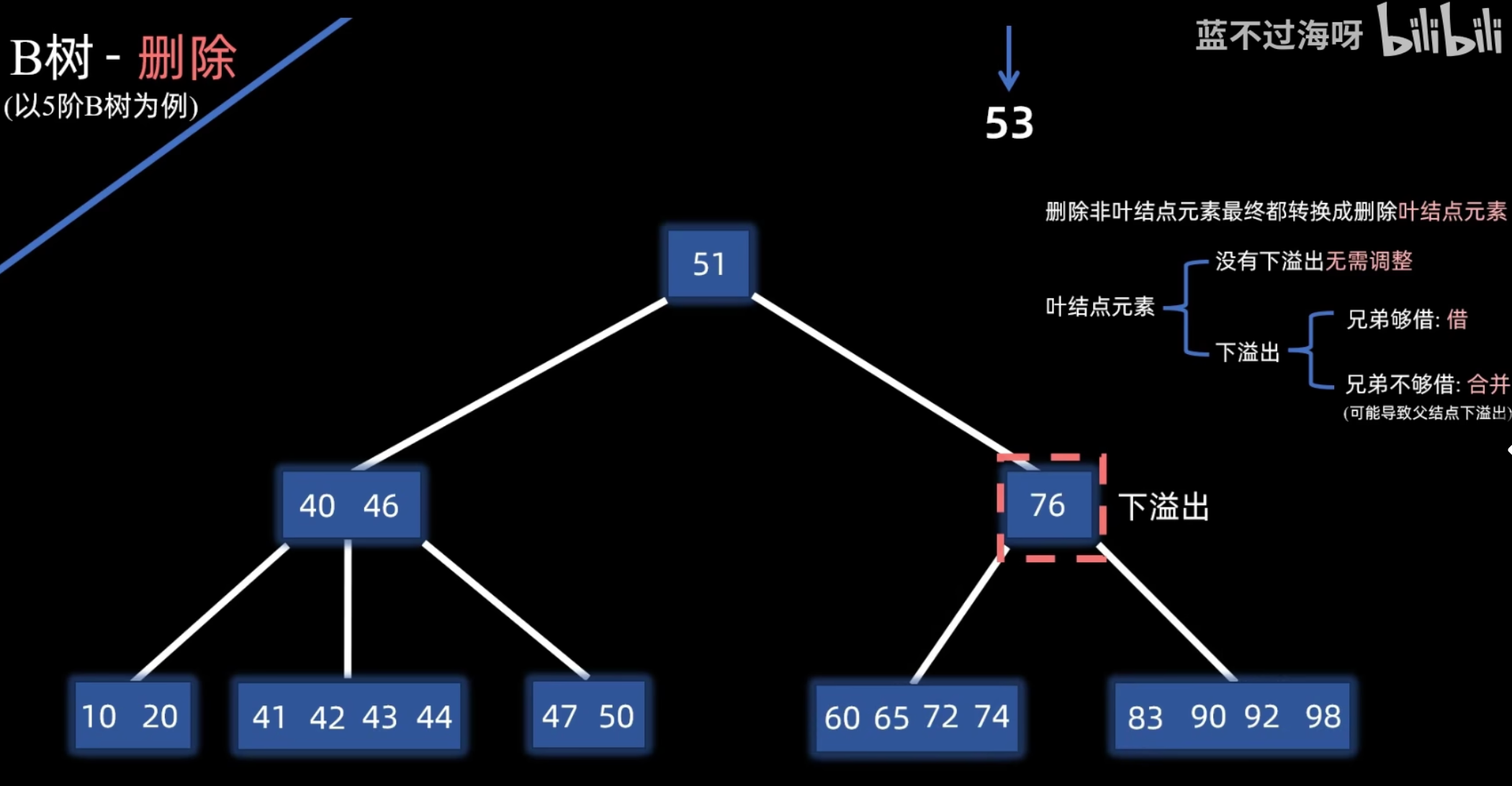
删除
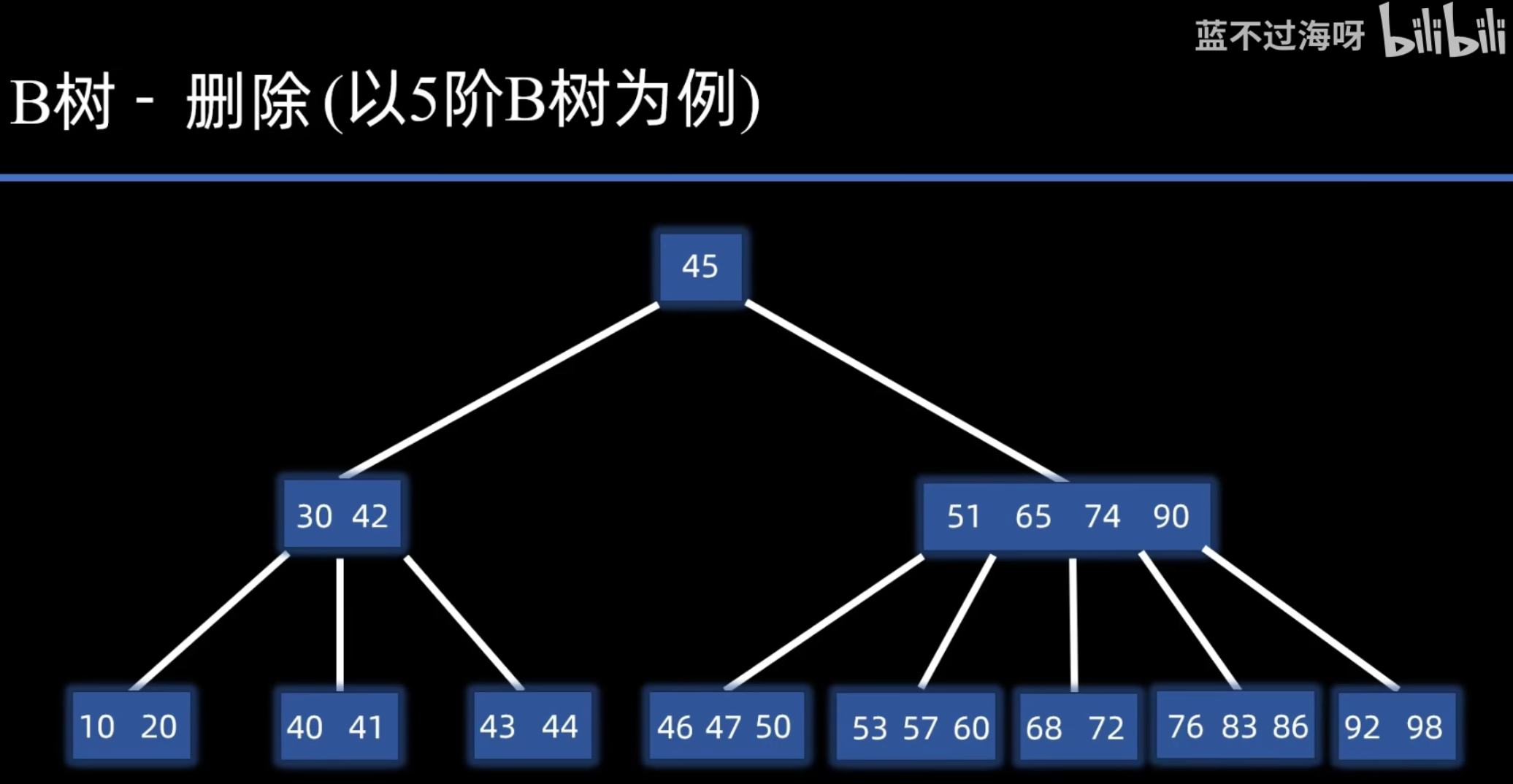
删除操作比插入复杂,因为它可能需要合并 (Merge) 或 借用 (Borrow) 关键字来维持 B 树的性质。
-
定位:找到包含待删除关键字 的结点。
-
处理删除:
- Case 1: 位于叶子结点
- 情况 1a (结点富余):若删除 后,该结点的关键字数仍 ,直接删除。
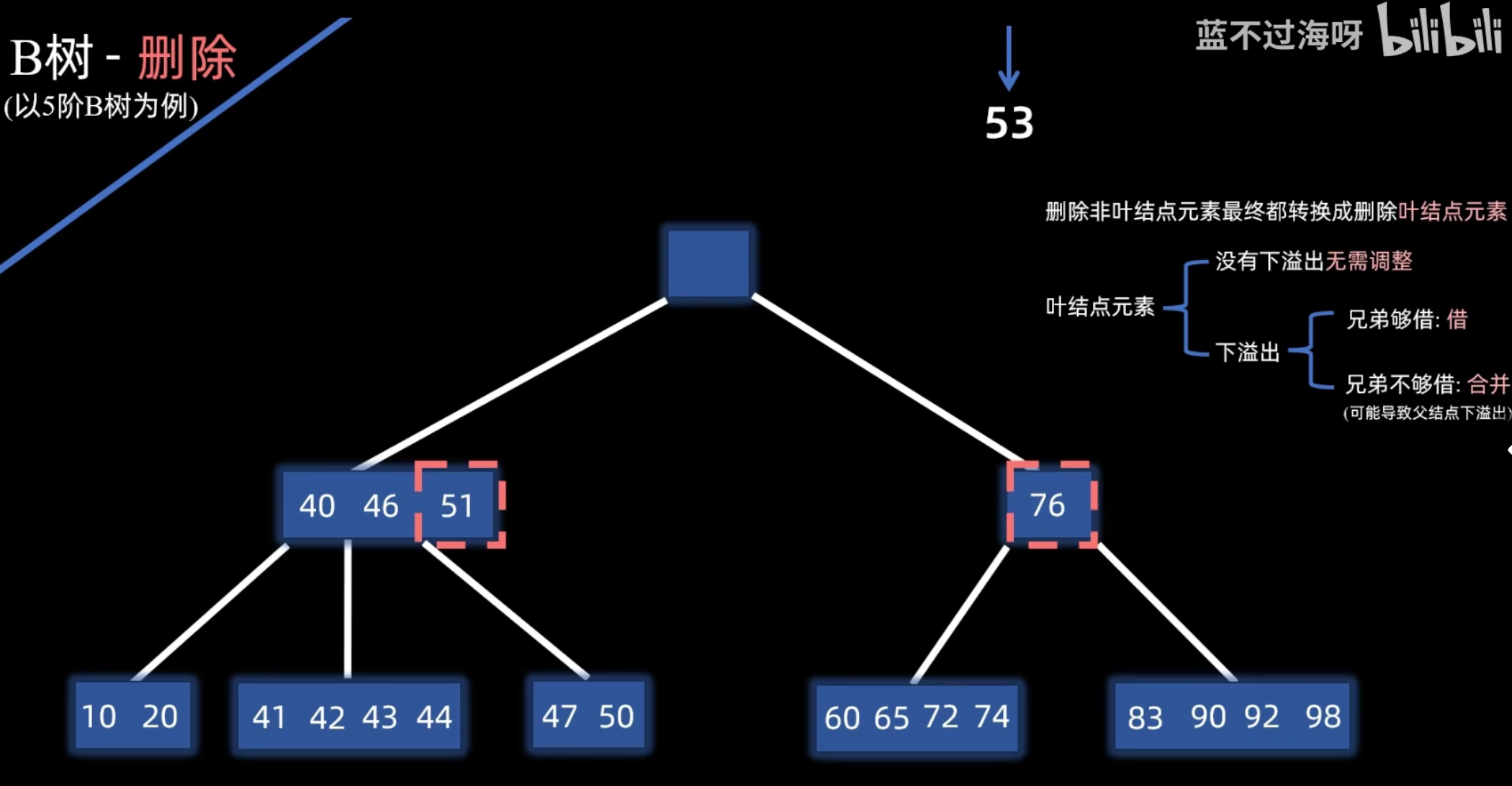
- 情况 1b (结点下溢):若删除 后,该结点的关键字数 ,则需要调整:
- 借用:检查其左右兄弟结点。若某兄弟结点关键字数 > ,则从该兄弟结点“借”一个关键字。具体操作是:将父结点中与该兄弟相邻的关键字下移到当前结点,再将兄弟结点中的一个相应关键字上移到父结点。
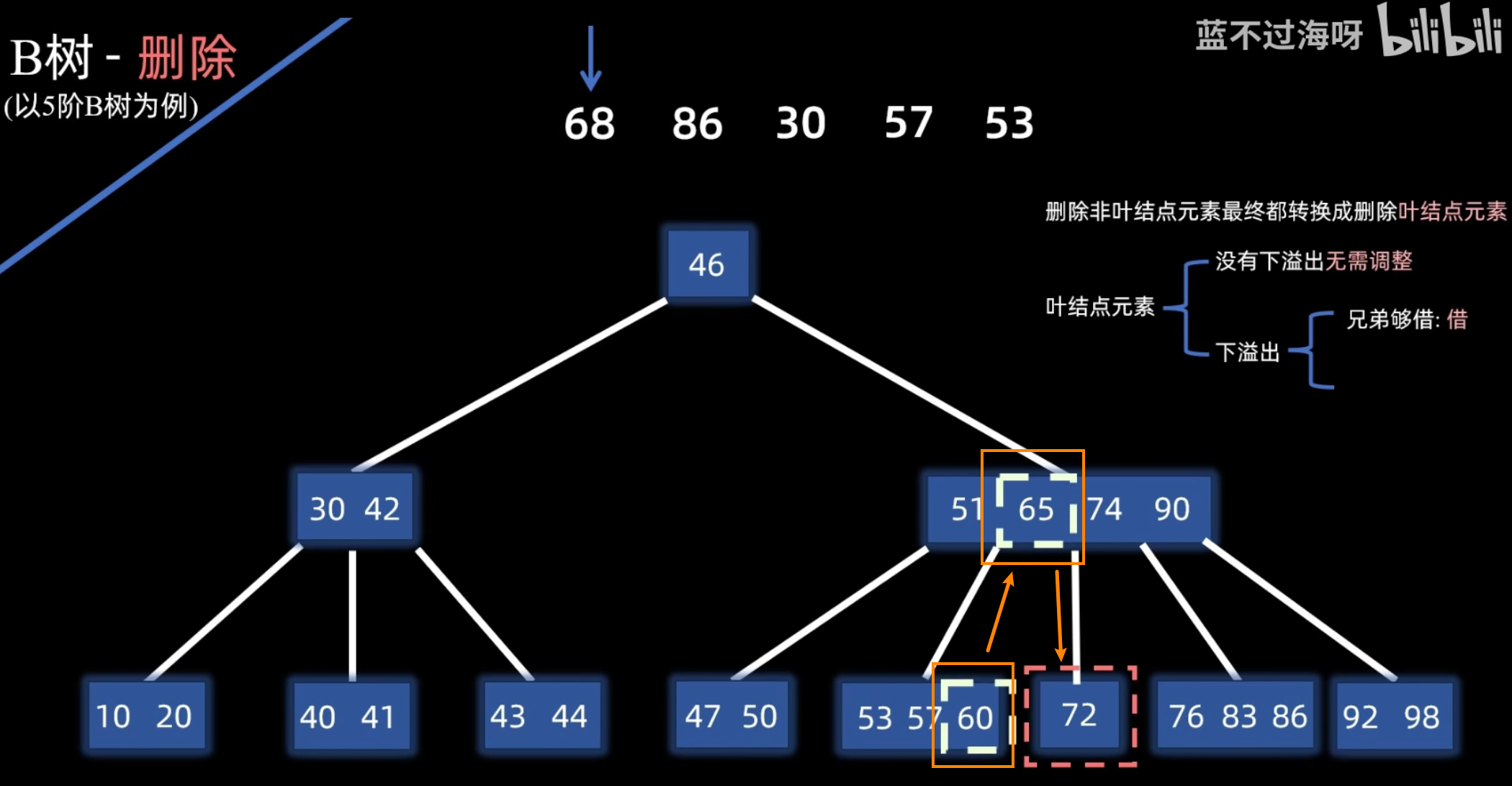
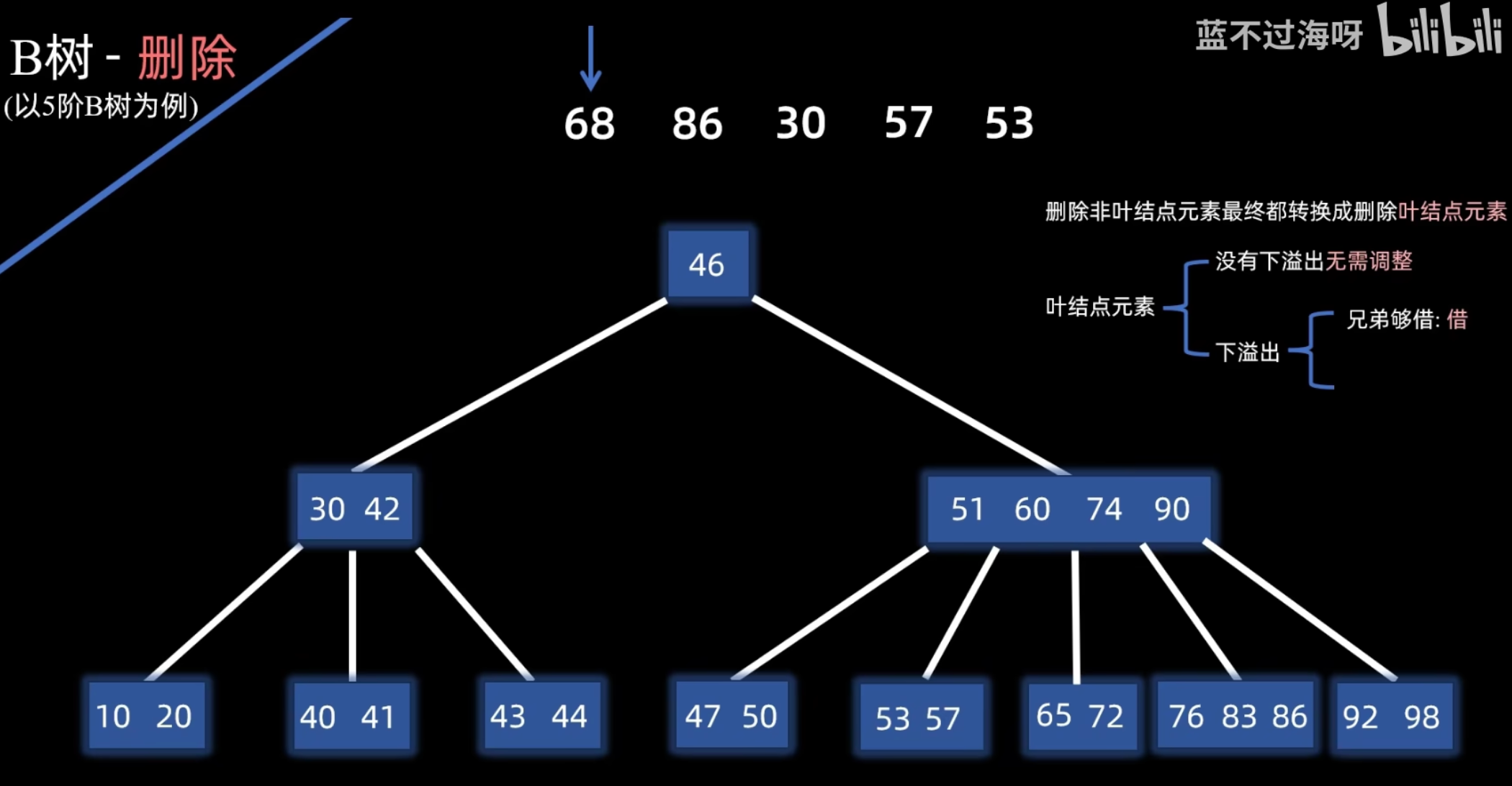
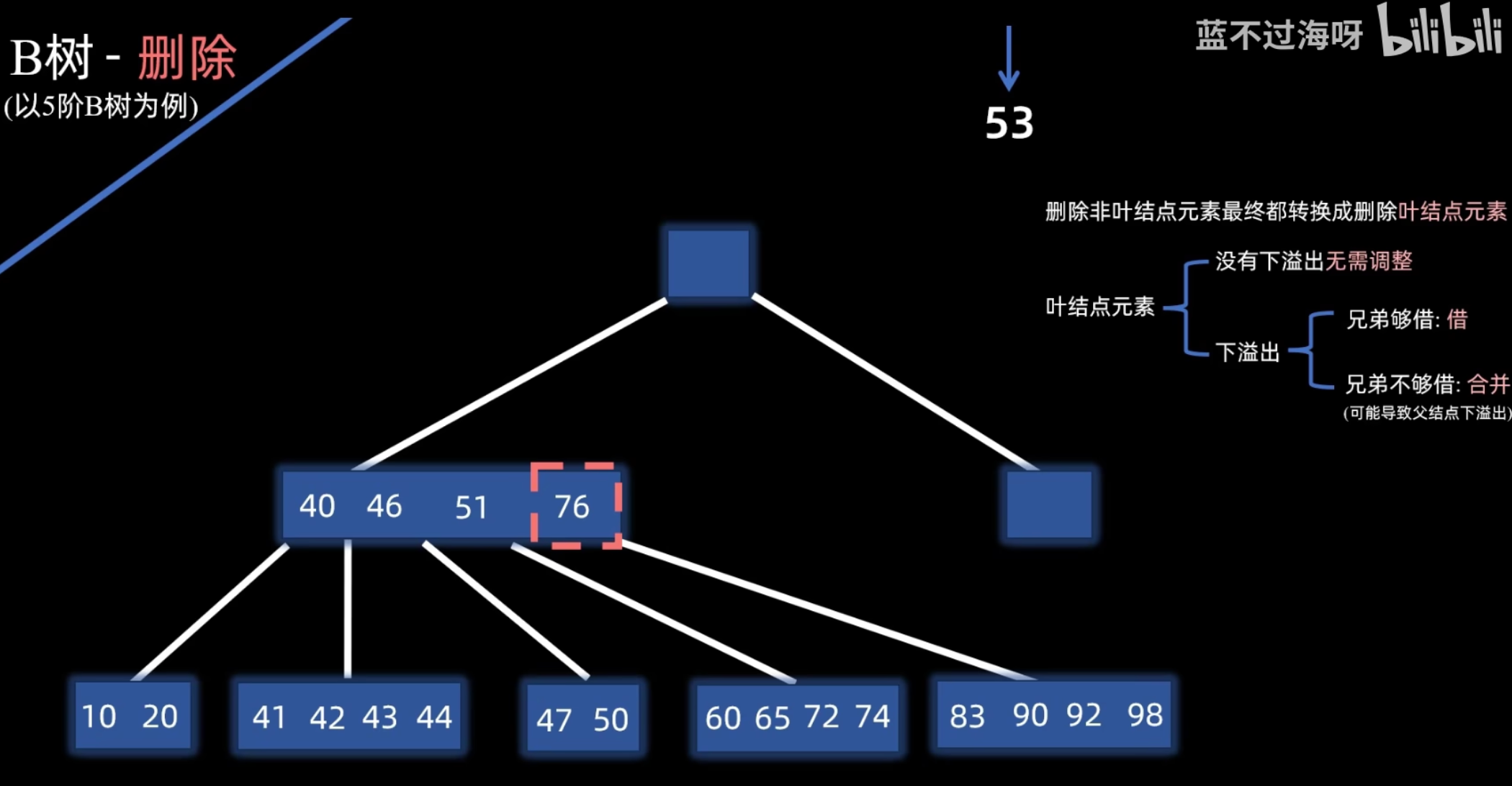
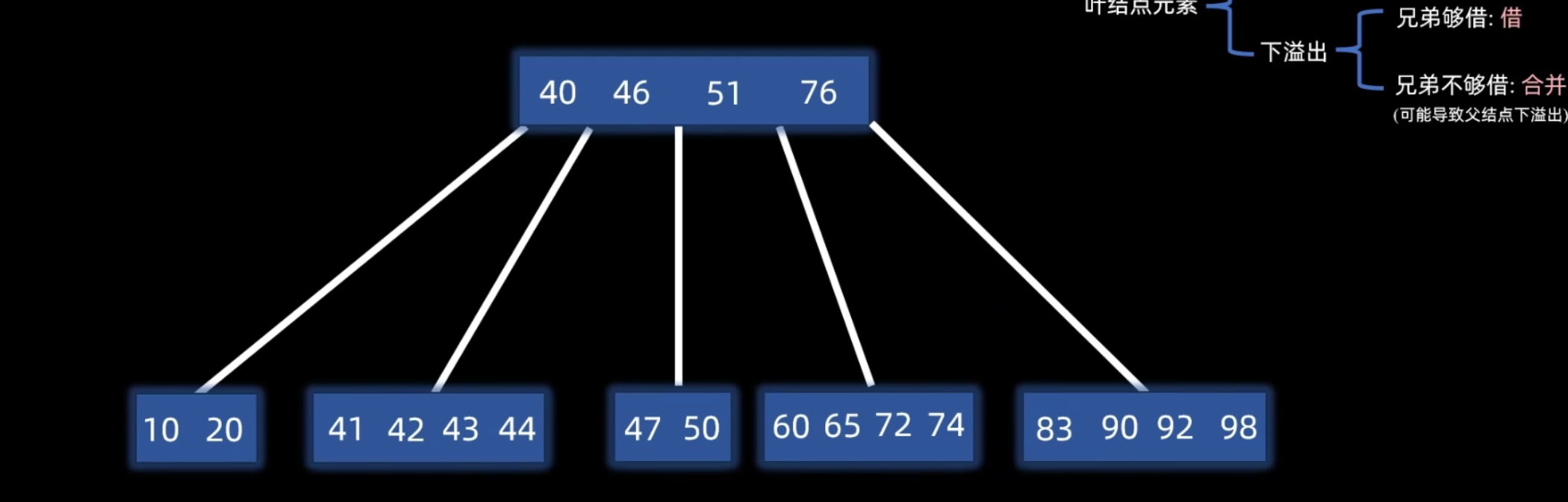
- 合并:若左右兄弟结点都无法借用(关键字数均为 ),则将当前结点、其一侧的兄弟结点以及父结点中分隔它们的关键字合并成一个新结点。
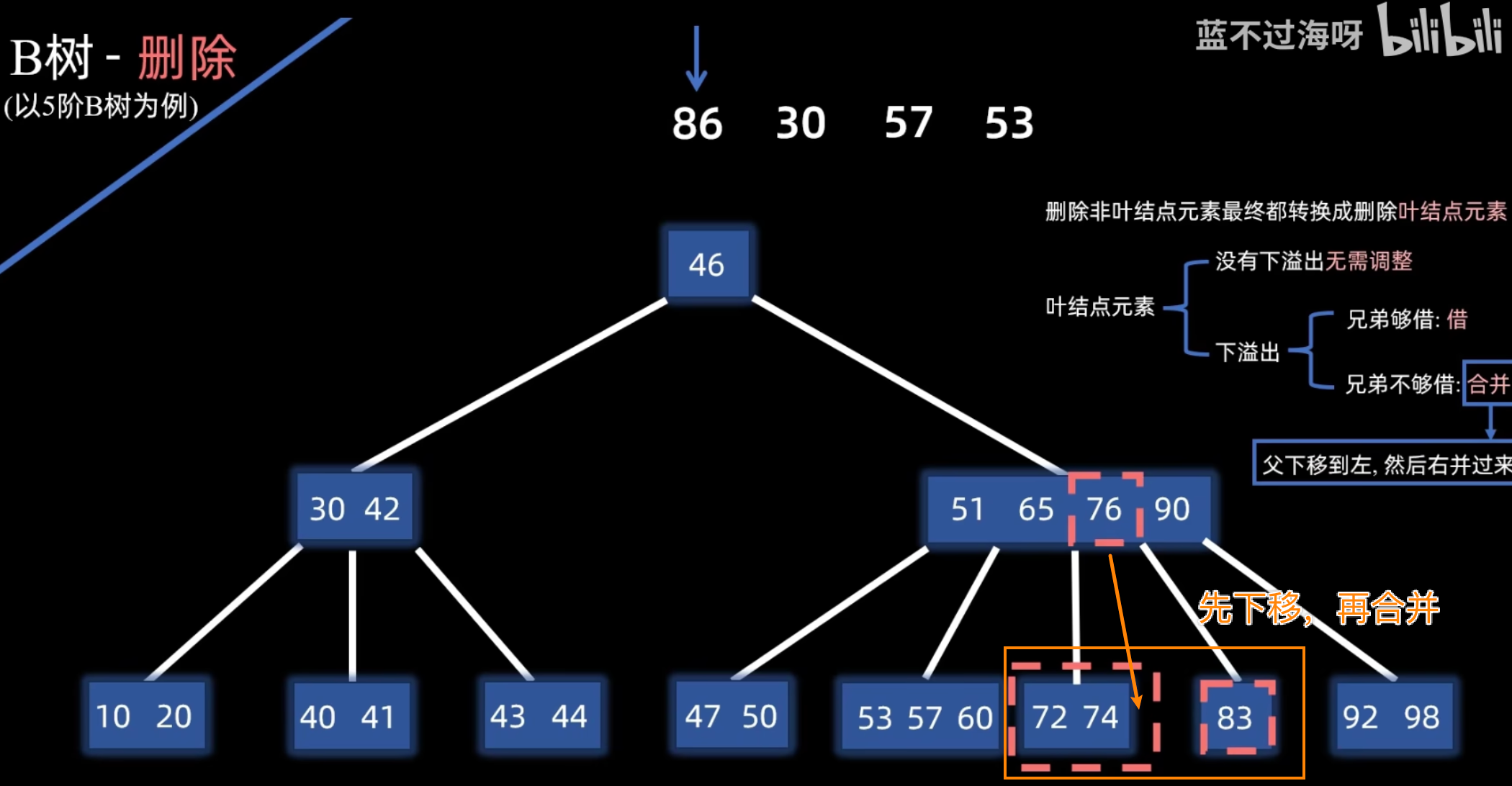
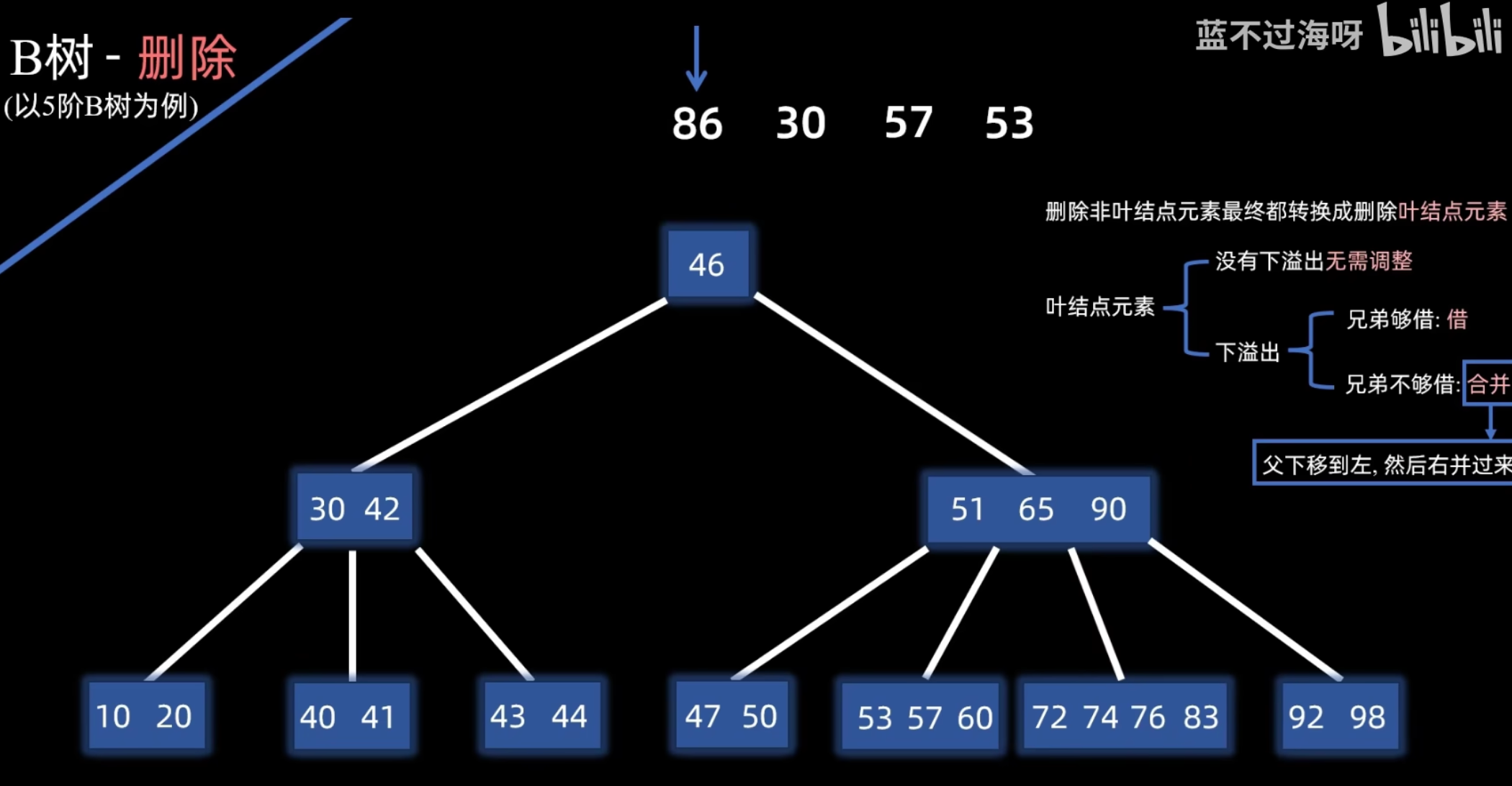
- 借用:检查其左右兄弟结点。若某兄弟结点关键字数 > ,则从该兄弟结点“借”一个关键字。具体操作是:将父结点中与该兄弟相邻的关键字下移到当前结点,再将兄弟结点中的一个相应关键字上移到父结点。
- Case 2: 位于非叶子结点
- 用 的直接前驱或直接后继关键字(它们必定在叶子结点中)来替代 的位置。
- 然后,将被用来替换的那个前驱或后继关键字从其所在的叶子结点中删除。
- 这个问题就转化为了 Case 1 的情况。
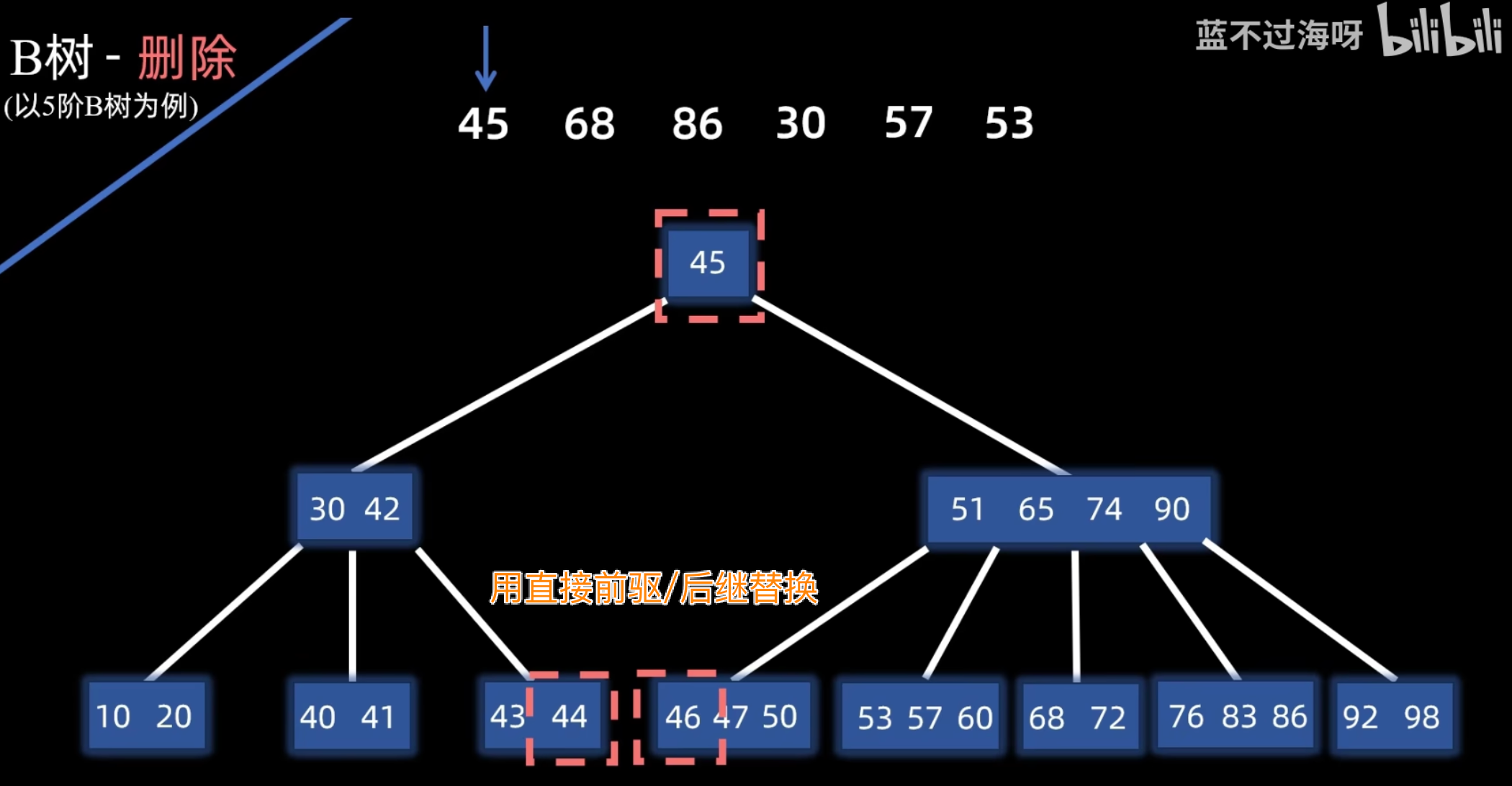
- Case 1: 位于叶子结点
-
递归调整:如果合并操作导致父结点发生下溢,则对父结点递归执行相同的调整策略(借用或合并)。此过程可能一直向上传播到根。如果根结点的最后一个关键字被下移导致根变空,则树的高度减 1。
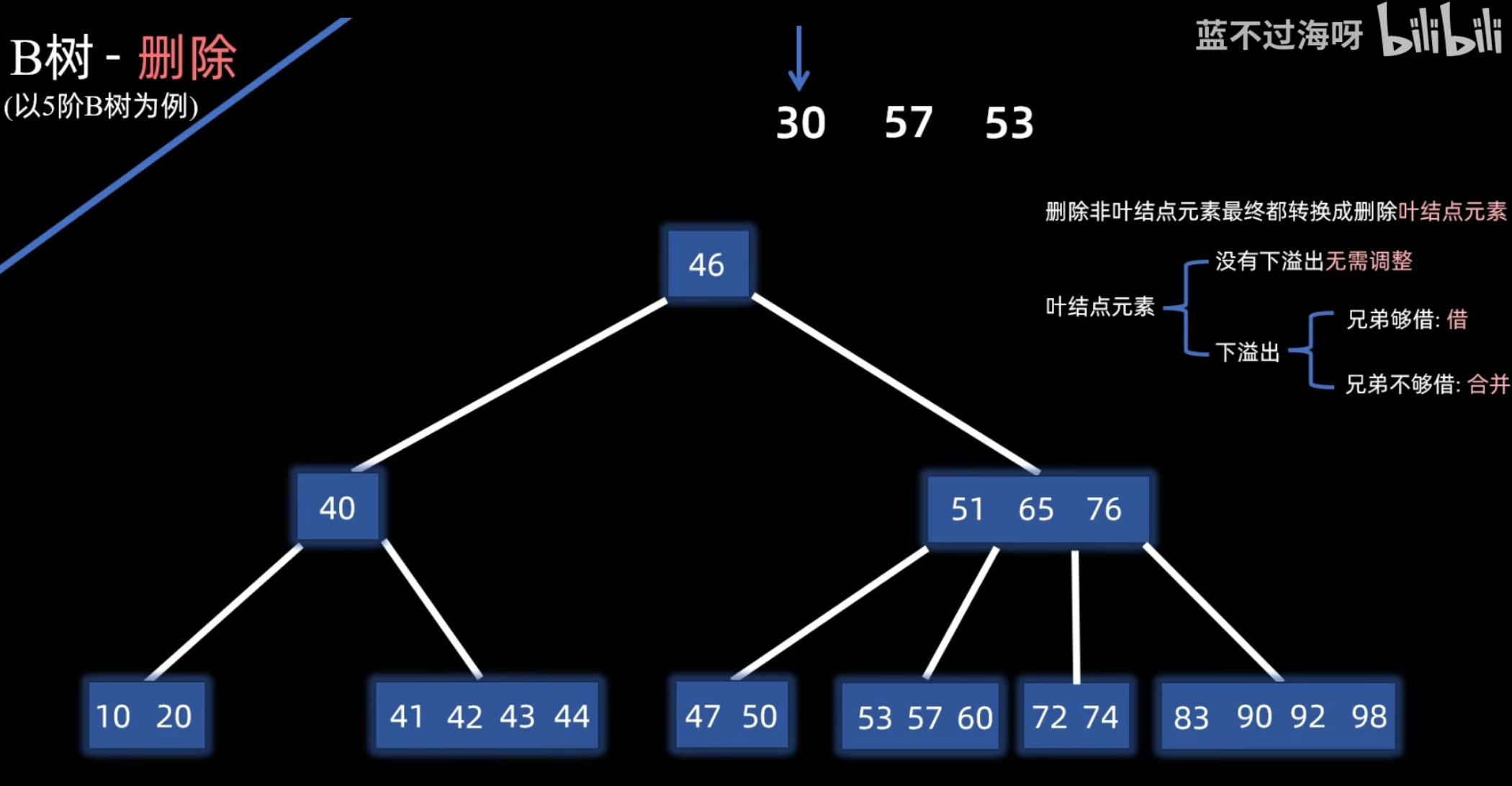
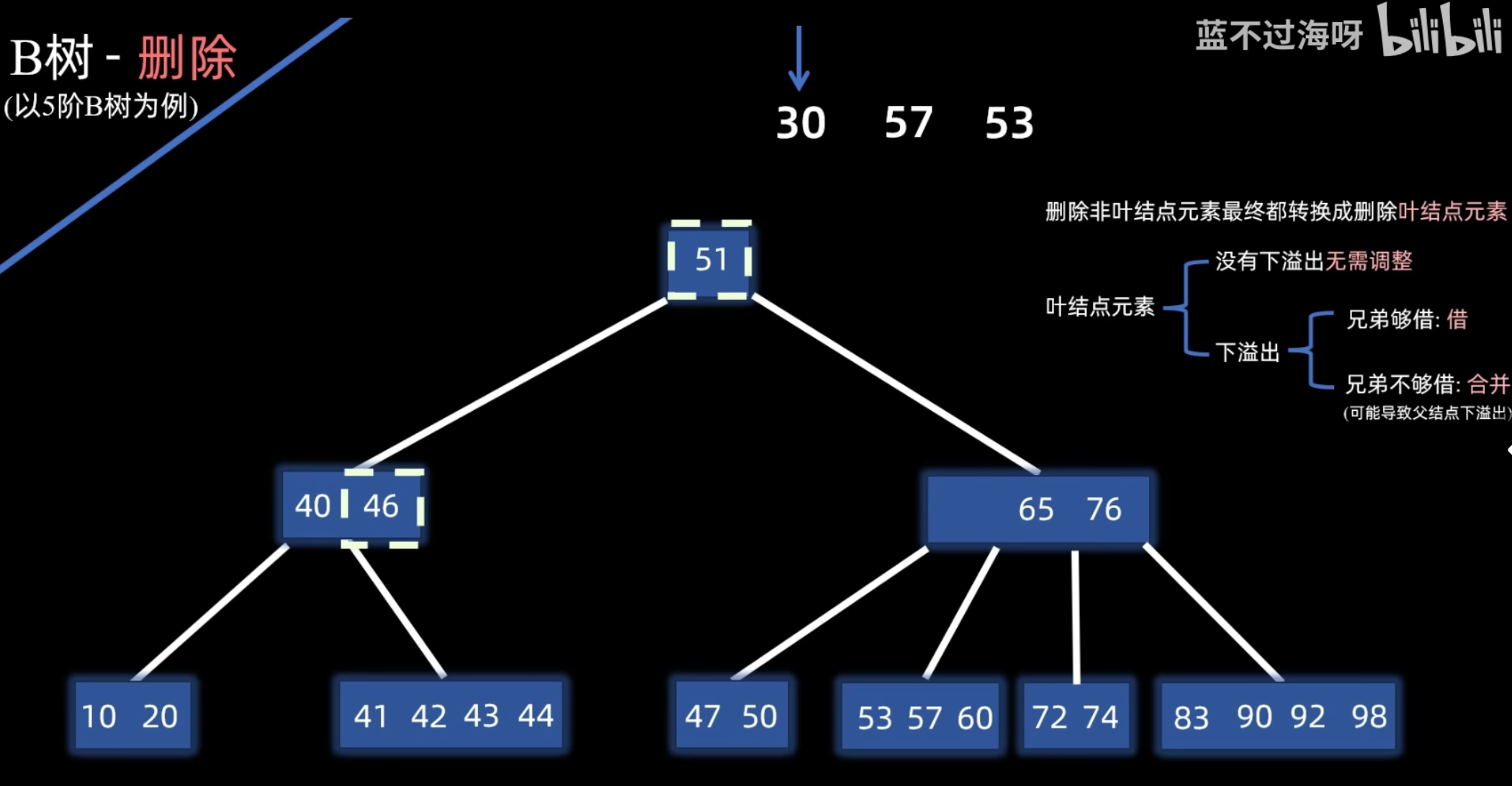 ![[attachment/4511ebb82ecb8fce8d9abe0010b63a85_MD5.png|注意兄弟节点的左子树也需要借过来]]
![[attachment/4511ebb82ecb8fce8d9abe0010b63a85_MD5.png|注意兄弟节点的左子树也需要借过来]]