101 绪论

1. 基本概念

定义

• 在任何问题中，数据元素都不是孤立存在的，而是在它们之间存在着某种关系，这种数据元素相互之间的关系称为结构（Structure）。数据结构是相互之间存在一种或多种特定关系的数据元素的集合。数据结构包括三方面的内容：逻辑结构、存储结构和数据的运算。数据的逻辑结构和存储结构是密不可分的两个方面，一个算法的设计取决于所选定的逻辑结构，而算法的实现依赖于所采用的存储结构。

逻辑结构

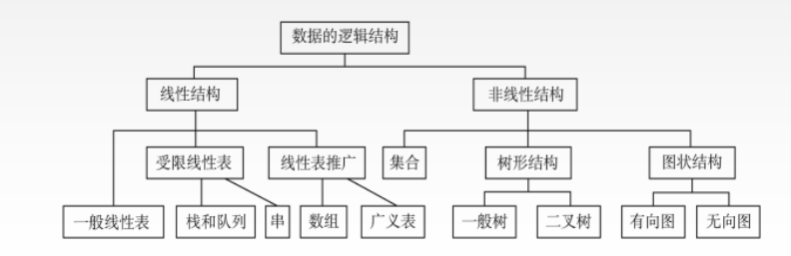
• 逻辑结构是指数据元素之间的逻辑关系，即从逻辑关系上描述数据。它与数据的存储无关，是独立于计算机的
• 数据的逻辑结构分为线性结构和非线性结构
  • 集合结构中的数据元素之间除了“同属于一个集合”的关系外，别无其他关系。 类似于数学上的集合
  • 线性结构结构中的数据元素之间只存在一对一的关系。比如排队
  • 树形结构结构中的数据元素之间存在一对多的关系。比如家族族谱
  • 图状结构或网状结构 结构中的数据元素之间存在多对多的关系。 比如地图

物理结构

• 存储结构是指数据结构在计算机中的表示（又称映像），也称物理结构。它包括数据元素的表示和关系的表示。数据的存储结构是逻辑结构用计算机语言的实现，它依赖于计算机语言。数据的存储结构主要有：顺序存储、链式存储、索引存储和散列存储。
  • 顺序存储：存储的物理位置相邻。（p.s. 物理位置即信息在计算机中的位置。）
  • 链接存储：存储的物理位置未必相邻，通过记录相邻元素的物理位置来找到相邻元素。
  • 索引存储：类似于目录，以后可以联系操作系统的文件系统章节来理解。
  • 散列存储：通过关键字直接计算出元素的物理地址（以后详解）。

算法的五个特征

1. 有穷性：有限步之后结束
2. 确定性：不存在二义性，即没有歧义
3. 可行性：比如受限于计算机的计算能力，有些算法虽然理论上可行，但实际上无法完成。
4. 输入：能被计算机处理的各种类型数据，如数字，音频，图像等等。
5. 输出：一至多个程序输出结果。

算法的复杂度

• 时间复杂度：
  • 它用来衡量算法随着问题规模增大，算法执行时间增长的快慢；
  • 是问题规模的函数：$T(n)$ 是时间规模函数，时间复杂度主要分析 $T(n)$ 的数量级
  • $T(n)=O(f(n))f(n)$ 是算法中基本运算的频度 一般我们考虑最坏情况下的时间复杂度
• 空间复杂度：
  • 它用来衡量算法随着问题规模增大，算法所需空间的快慢；
  • 是问题规模的函数：$S(n)=O(g(n))$ ；算法所需空间的增长率和 $g(n)$ 的增长率相同。

概要: 复杂度计算为重点

• 常用的时间复杂度大小关系：
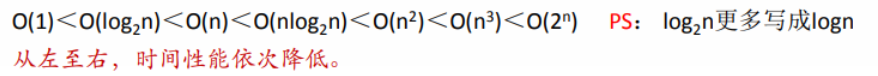
• 复杂度如何计算
  • 时间复杂度计算（单个循环体）
    • 直接关注循环体的执行次数，设为 k
  • 时间复杂度计算（多个循环体）
    • 两个运算规则：乘法规则，加法规则。