反三角函数
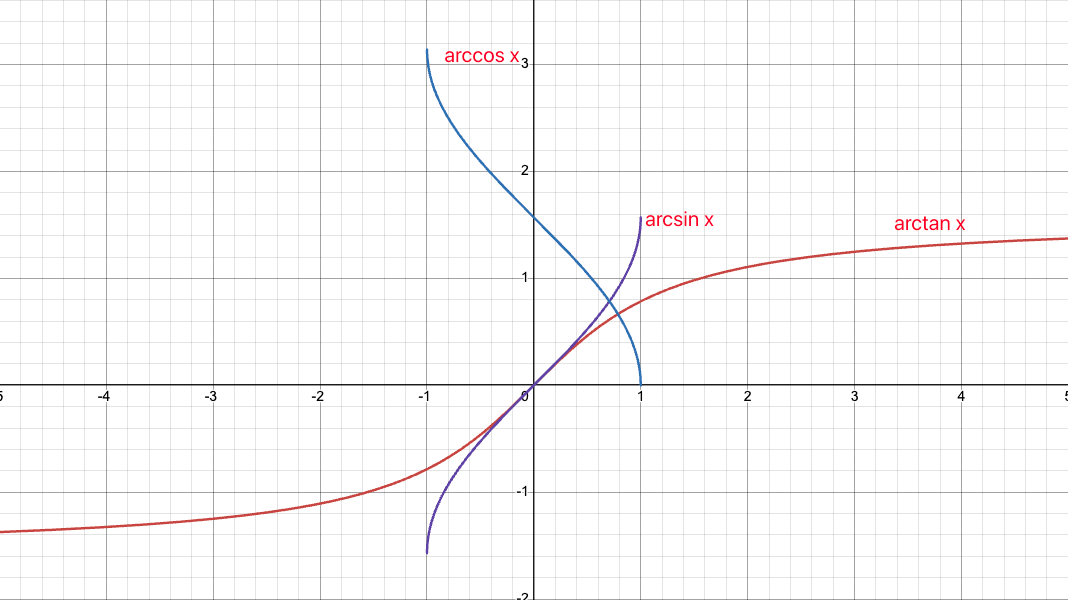
1. arcsin(x)
- 定义: 是反正弦函数,表示正弦值为 x 的角。如果 ,且 ,那么 。通常也记作 。
- 定义域: 。
- 值域: 。
- 奇偶性: 奇函数,即
- 单调性: 在其定义域 上是增函数 。
- 导数:
- 推导过程:
- 设 ,则 。
- 两边对 x 求导: 。
- 所以 。
- 因为 ,且 ,所以 。
- 因此, 。
- 推导过程:
- 重要性质与恒等式:
- 当 时成立:
- 当 时成立 。对于其他 x 值,,其中 k 为整数,具体取决于 x 所在的区间以确保结果在 内 。
- 当 时成立 :
- 当 时成立 :
- 一些常见的 arcsin 值:
| x | arcsin(x) (弧度) | arcsin(x) (角度) |
|---|---|---|
| -1 | -90° | |
| -60° | ||
| -30° | ||
| 0 | 0 | 0° |
| 30° | ||
| 60° | ||
| 1 | 90° |
2. arccos(x)
- 定义: 是反余弦函数,表示余弦值为 x 的角。如果 ,且 ,那么 。通常也记作 。
- 定义域: 。
- 值域: 。
- 奇偶性: 非奇非偶函数 。有:
- 单调性: 在其定义域 上是减函数 。
- 导数:
- 推导过程:
- 设 ,则 。
- 两边对 x 求导: 。
- 所以 。
- 因为 ,且 ,所以 。
- 因此, 。
- 推导过程:
- 重要性质与恒等式:
- 当 时成立 :
- 当 时成立。对于其他 x 值, 或 ,其中 k 为整数,具体取决于 x 所在的区间以确保结果在 内 。
- 当 时成立 :
- 当 时成立 :
- 一些常见的 arccos 值:
| x | arccos(x) (弧度) | arccos(x) (角度) |
|---|---|---|
| -1 | 180° | |
| 150° | ||
| 120° | ||
| 0 | 90° | |
| 60° | ||
| 30° | ||
| 1 | 0 | 0° |
3. arctan(x)
- 定义: 是反正切函数,表示正切值为 x 的角。如果 ,那么 。通常也记作 。
- 定义域: 所有实数 ,即 。
- 值域: 。选择这个区间是为了保证函数的单值性和连续性 。
- 奇偶性: 奇函数,即
- 单调性: 在其定义域 上是增函数。
- 导数:
- 推导过程:
- 设 ,则 。
- 两边对 x 求导: 。
- 所以 。
- 利用恒等式 ,可得 。
- 因此, 。
- 推导过程:
- 重要性质与恒等式:
- 对所有实数 x 成立 :
- 当 时成立。对于其他 x 值,结果会有一个 的整数倍的平移。
- 如果 $xy < 1$ :$\arctan(x) + \arctan(y) = \arctan\left(\frac{x+y}{1-xy}\right)$
- 如果 $xy > -1$ :$\arctan(x) - \arctan(y) = \arctan\left(\frac{x-y}{1+xy}\right)$
- 一些常见的 arctan 值
| x | arctan(x) (弧度) | arctan(x) (角度) |
|---|---|---|
| (极限值) | -90° (极限值) | |
| -60° | ||
| -1 | -45° | |
| -30° | ||
| 0 | 0 | 0° |
| 30° | ||
| 1 | 45° | |
| 60° | ||
| (极限值) | 90° (极限值) |
4. arcsin(x) 和 arccos(x) 的关系
- 和 之间存在线性关系。
它们之间的关系可以用以下恒等式表示:
这个关系在其共同的定义域 内成立。
我们可以将这个恒等式改写成以下两种形式:
- 这两种形式都符合线性方程 的结构:
- 在形式 1 中,如果我们将 ,,自变量视为 ,常数项 。
- 在形式 2 中,如果我们将 ,,自变量视为 ,常数项 。
因此, 和 之间是线性关系。从图像上看, 的图像可以看作是将 的图像关于 x 轴对称(即乘以 -1),然后再向上平移 个单位得到的。这也意味着它们的图像关于直线 对称。