外部排序
基本概念
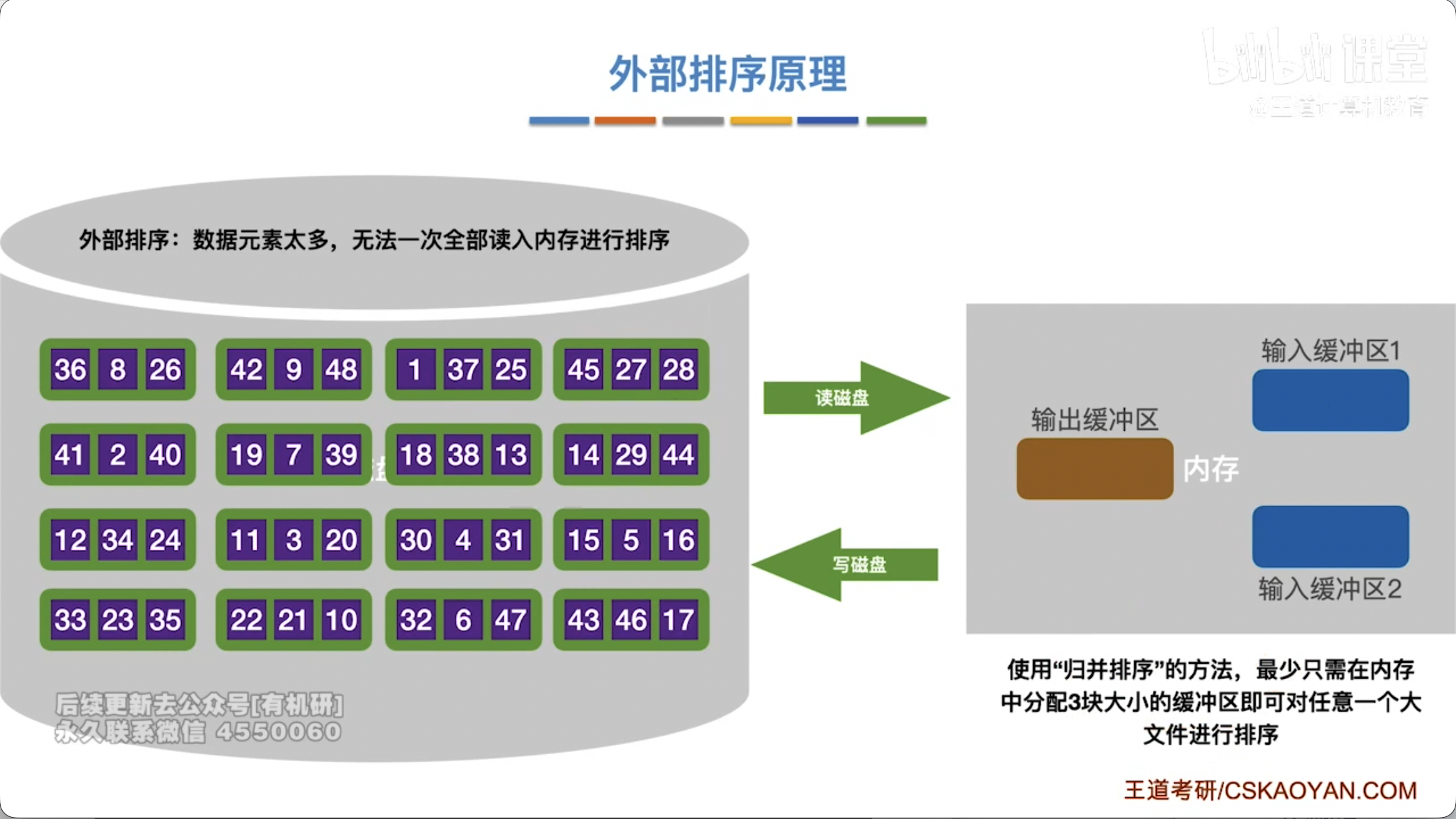
外部排序:在排序过程中,数据量过大,不能一次性载入内存,需要频繁访问外存的排序方式。
特点:
- 数据存储在外存(如磁盘)上。
- 排序过程涉及多次内存与外存之间的数据交换。
- 主要时间开销是磁盘 I/O 操作。
常用策略:分治法,将大文件分割成若干小文件,分别排序,然后进行归并。
外部排序的方法
1. 排序 - 归并策略:
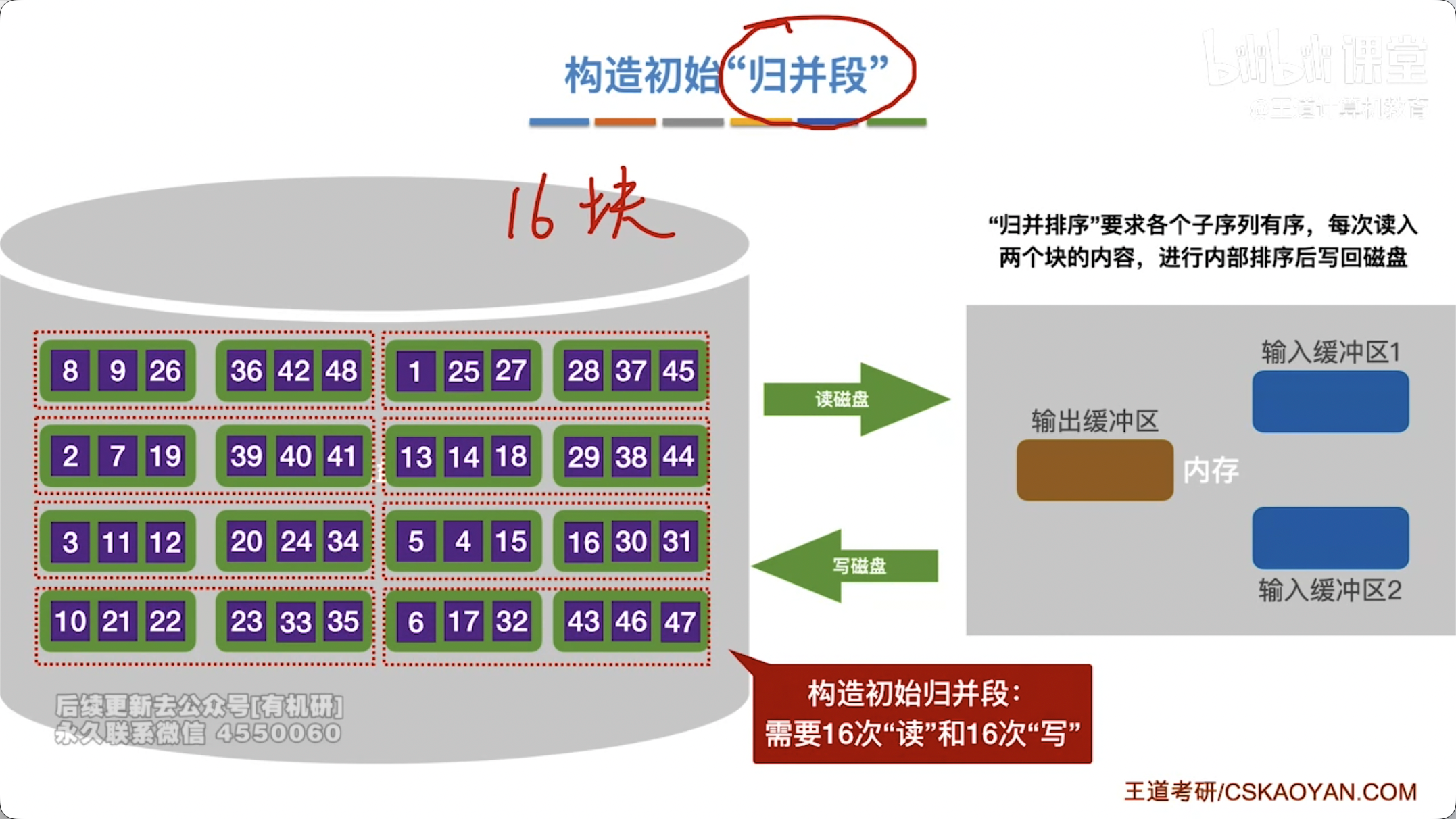
- 内部排序阶段:将大文件分割成若干个大小适中(能载入内存)的子文件(称为初始归并段或顺串),利用内部排序方法(如快速排序、堆排序等)对每个子文件进行排序。
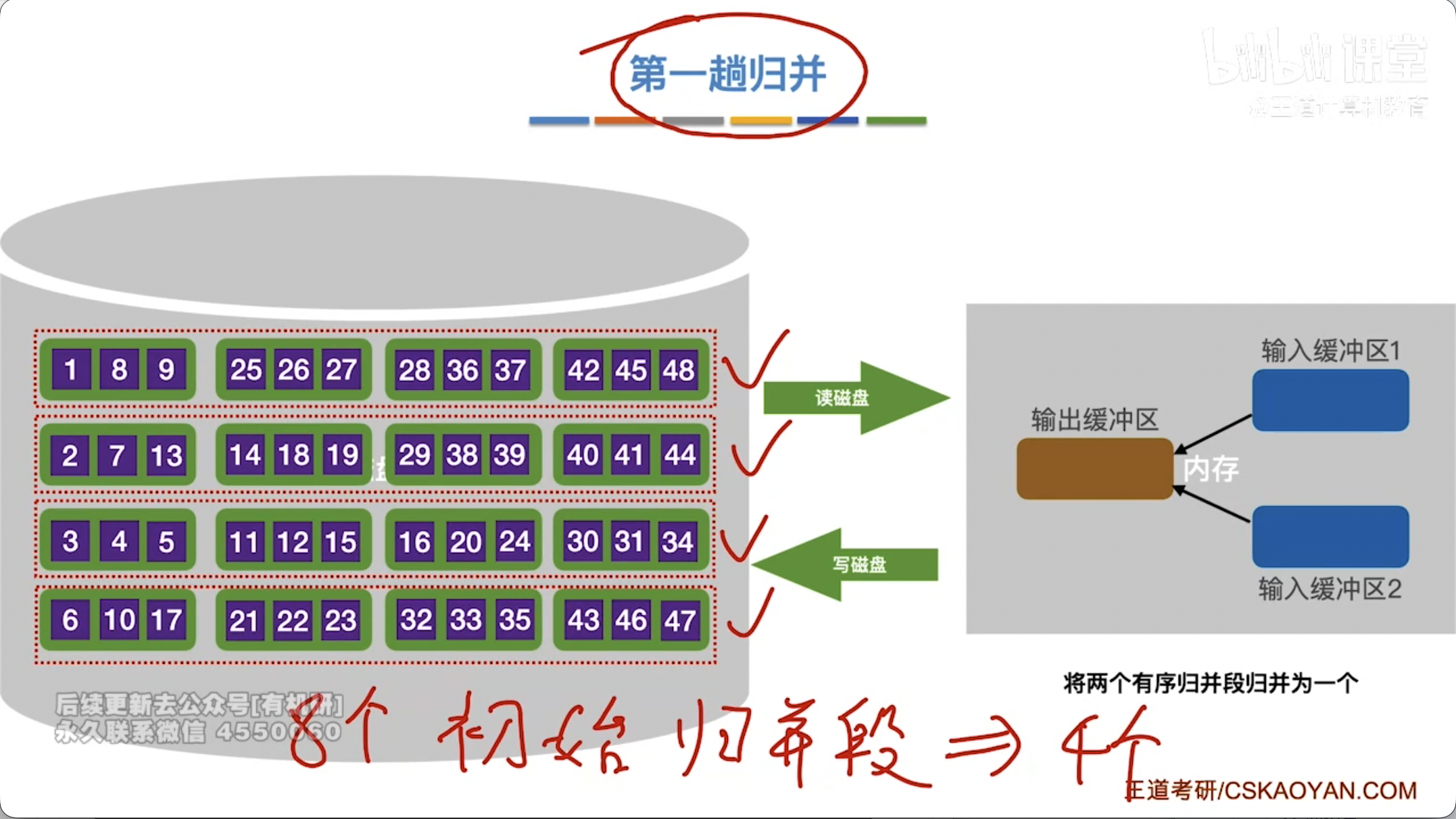
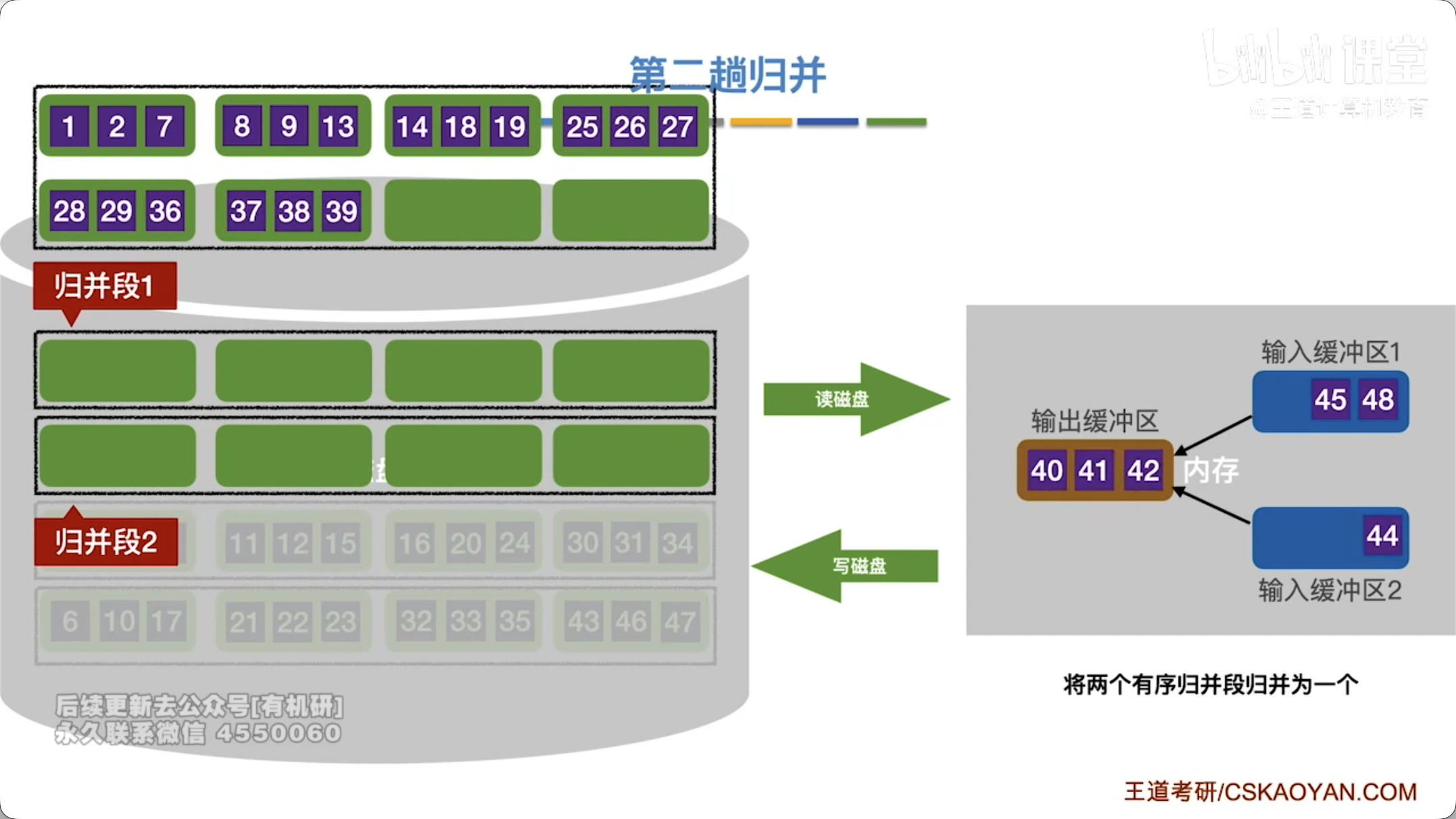
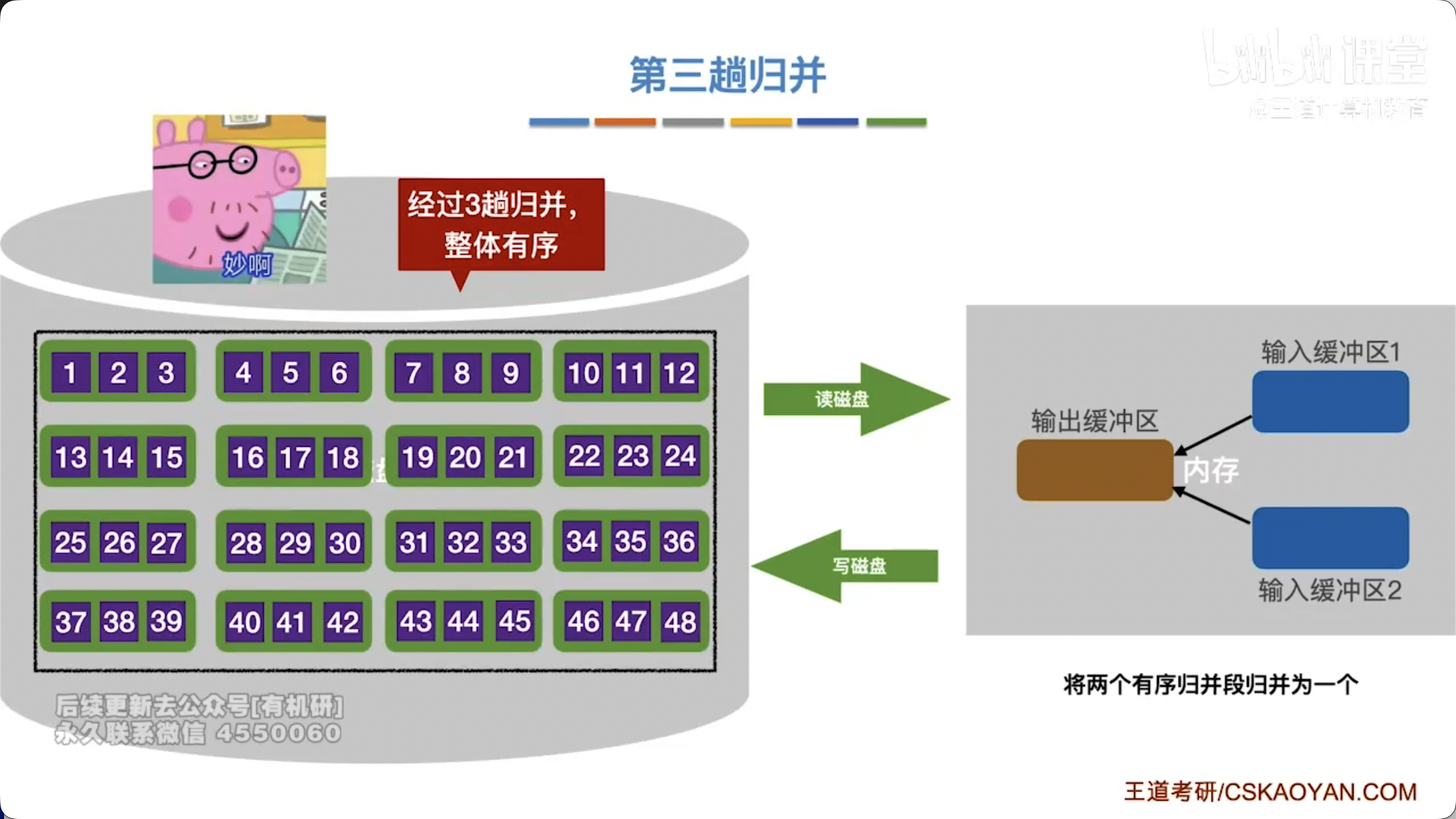
- 归并阶段:将已排序的初始归并段逐步进行多路平衡归并,直至所有数据归并成一个完全有序的文件。
2. 核心问题:
- 如何减少归并趟数?
- 增加归并路数 , 进行多路平衡归并 (但不能无限增加,因为自身也有开销)
- 减少初始归并段数量
- 如何进行高效的多路归并?(减少 I/O 次数)
多路平衡归并与败者树
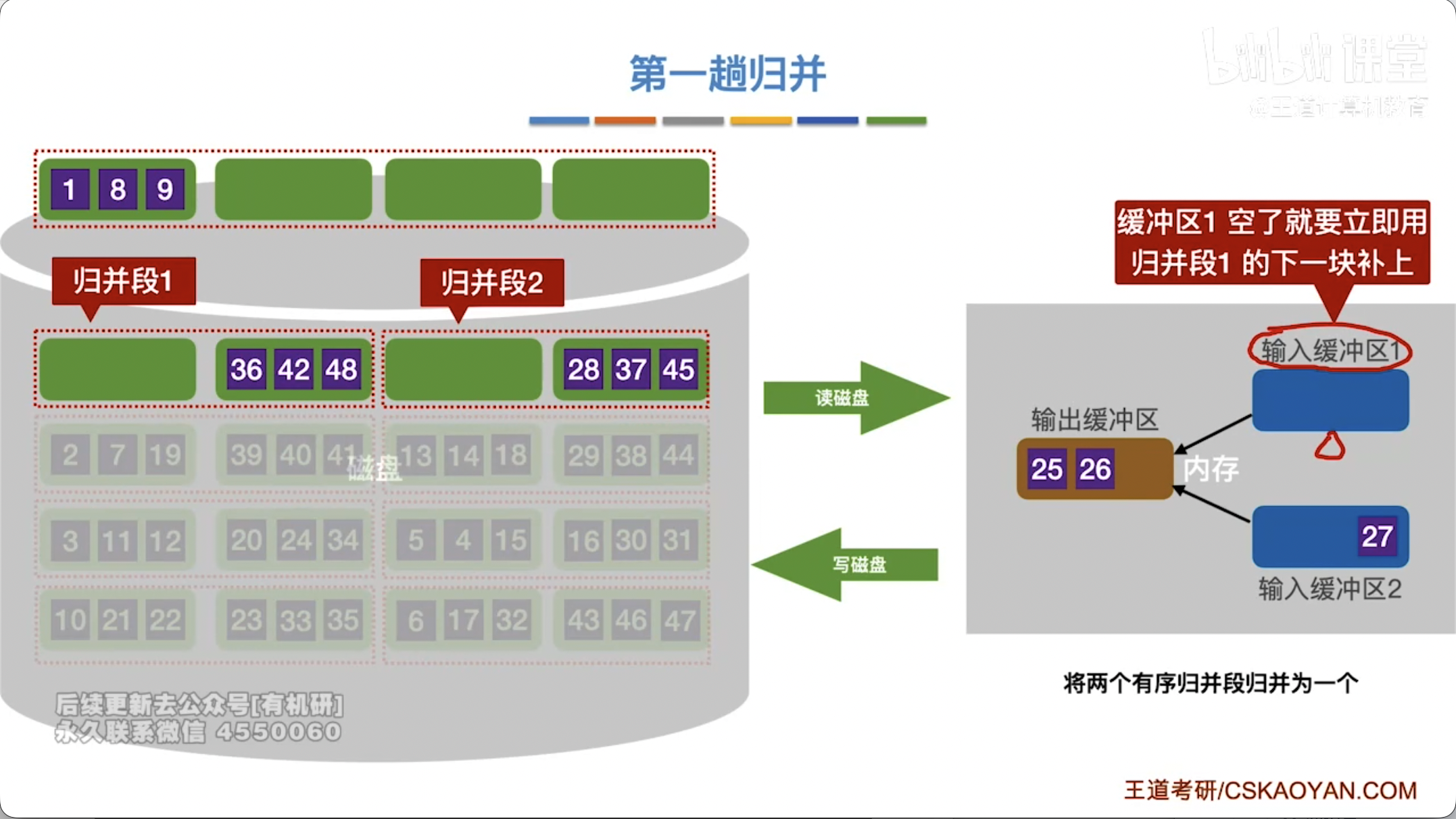
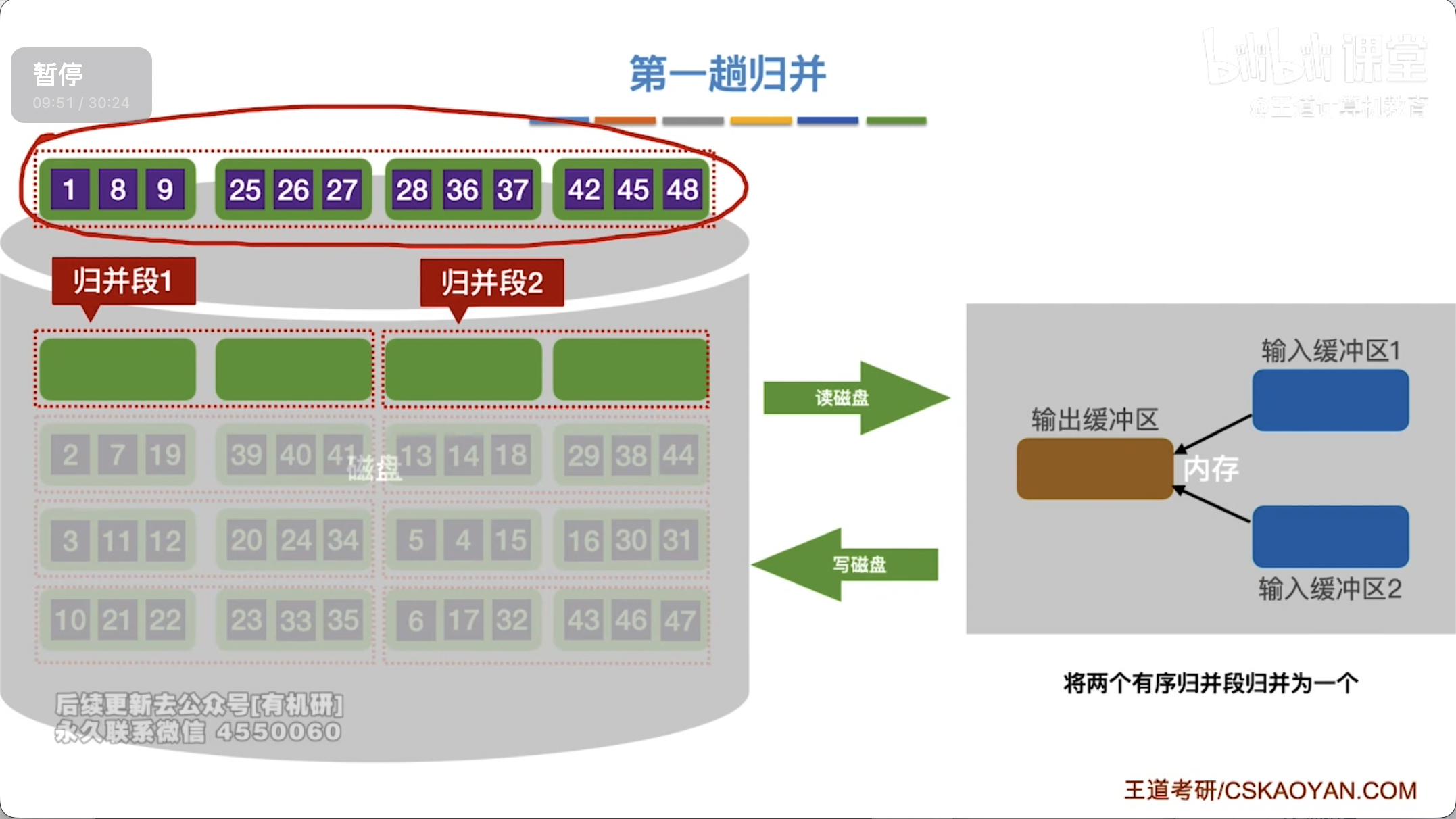
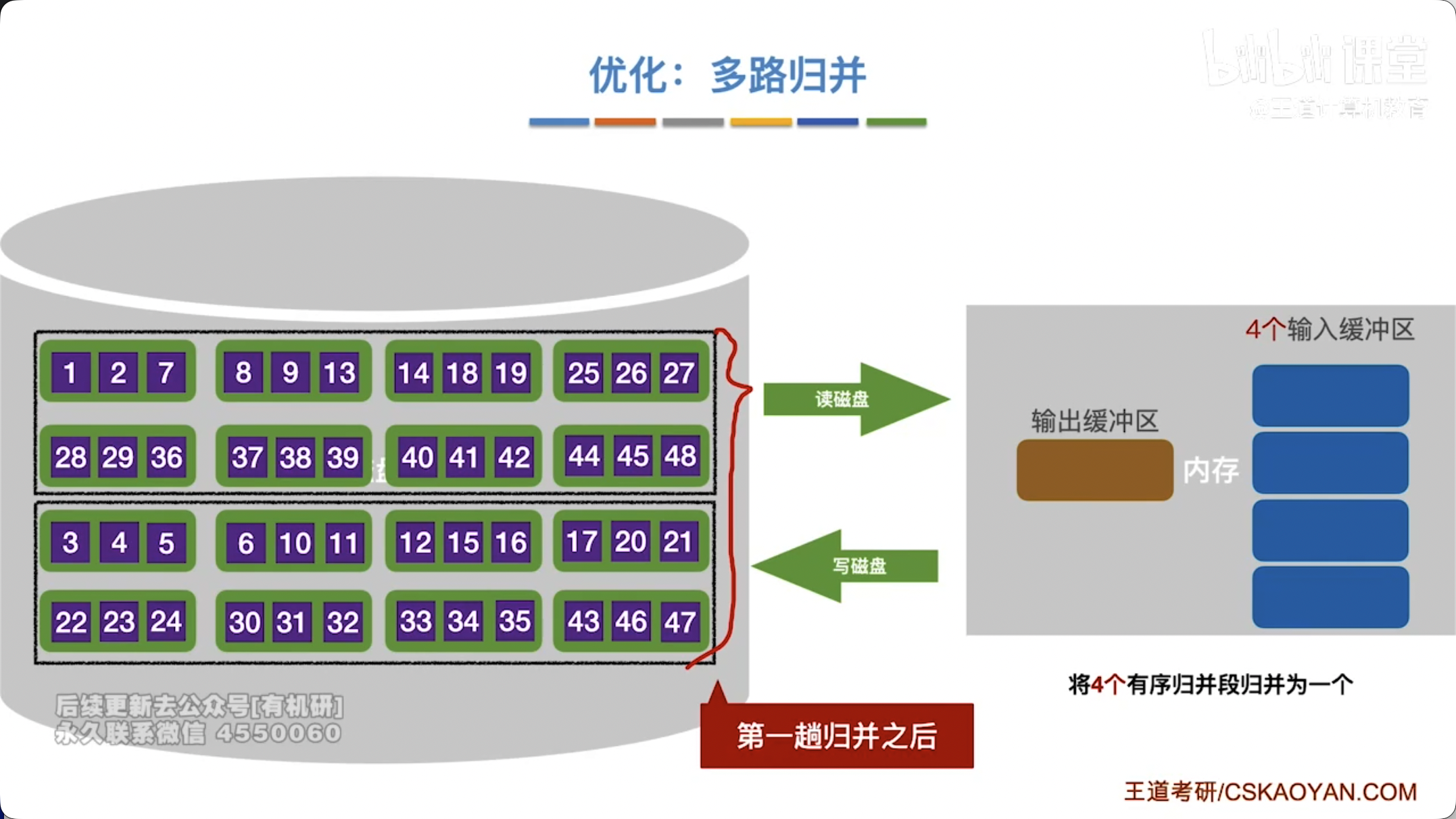
多路归并:
- 概念:将 个有序的初始归并段合并成一个有序段的过程。
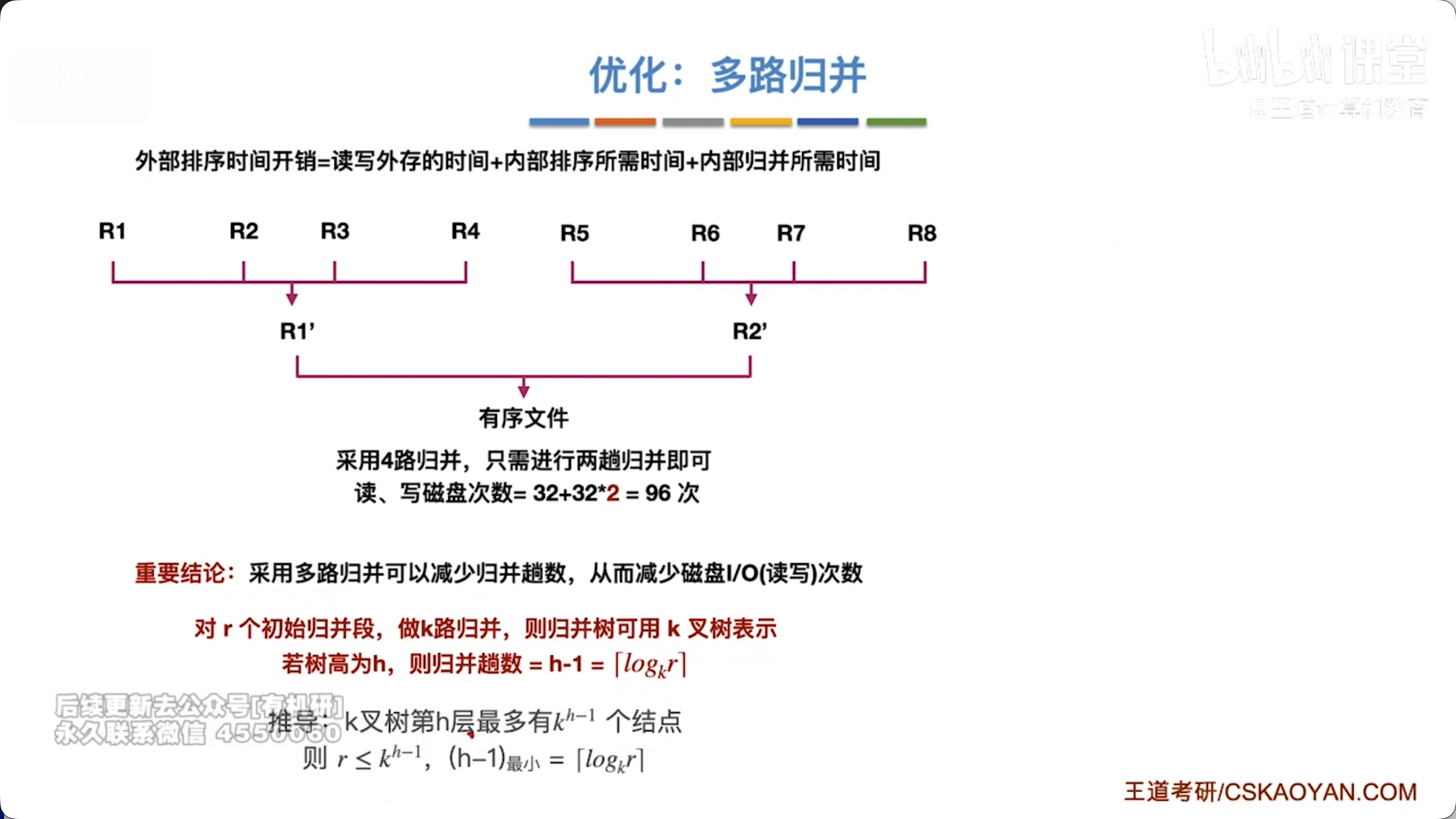
- 优点:与两路归并相比,减少了归并趟数。
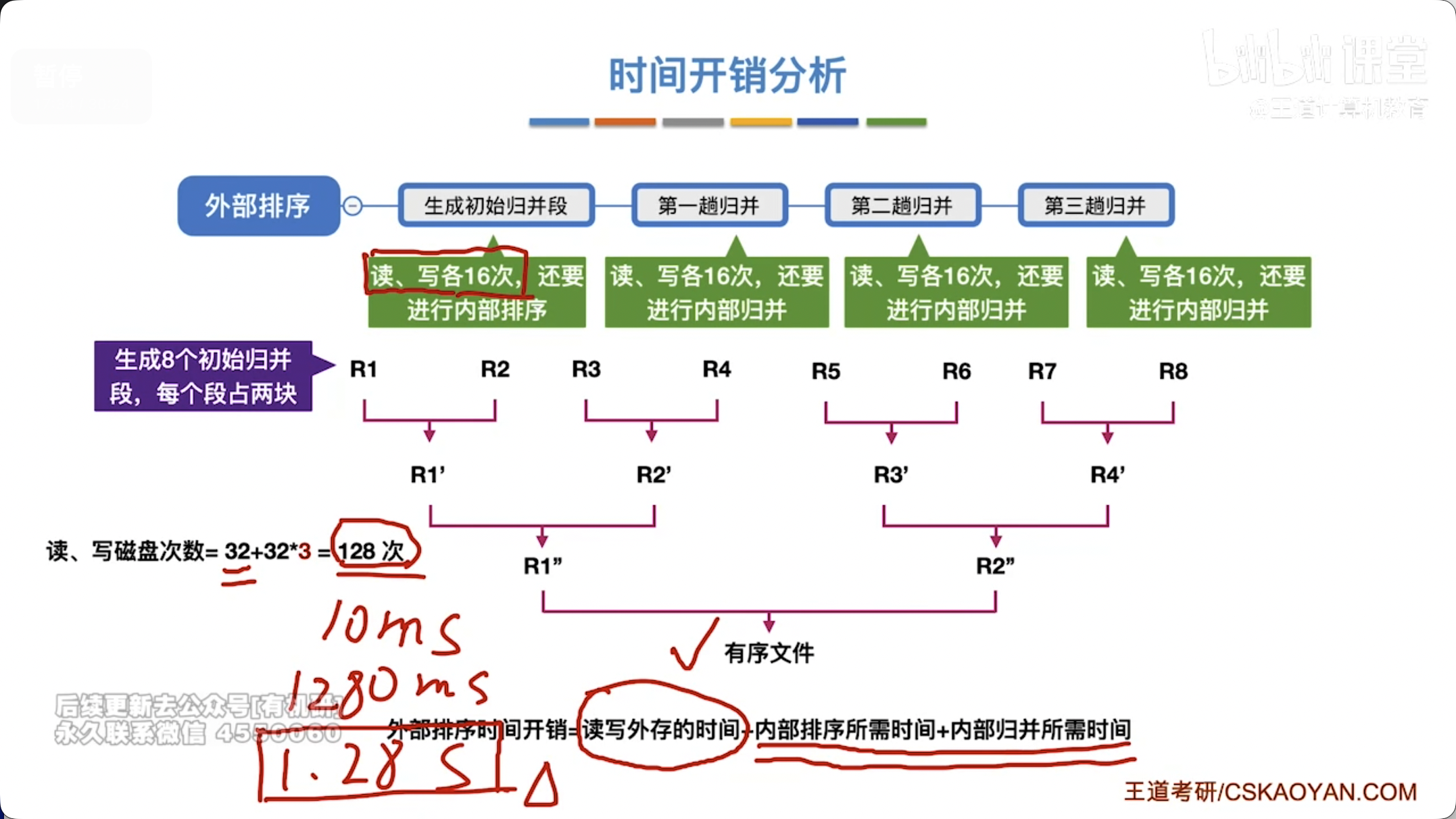
- 归并趟数计算:若初始归并段数量为 ,归并路数为 ,则归并趟数约为 。
- I/O 次数:每趟归并需要将所有数据读入内存一次,写回外存一次。因此,总的 I/O 次数与归并趟数成正比。

![[attachment/94017f0a8fc3c7f998ef0a35007fb23d_MD5.png|优化目标:减小归并趟数]]
![[attachment/64bd4f6a3af54800abbf6f90d9b0047b_MD5.png|归并路数不能无限大,有上限]]
平衡归并:
- 概念:在进行多路归并时,每次都将相同数量的归并段合并,以保持归并树的平衡,从而最小化总的归并趟数。
- 实现方式:
- 路平衡归并:每次从 个输入文件中各取一个元素,比较后选择最小的输出,直到某个文件为空,则该文件不再参与后续比较,从剩余文件中选择。当一个输出归并段完成时,开始新的归并段。
败者树的原理
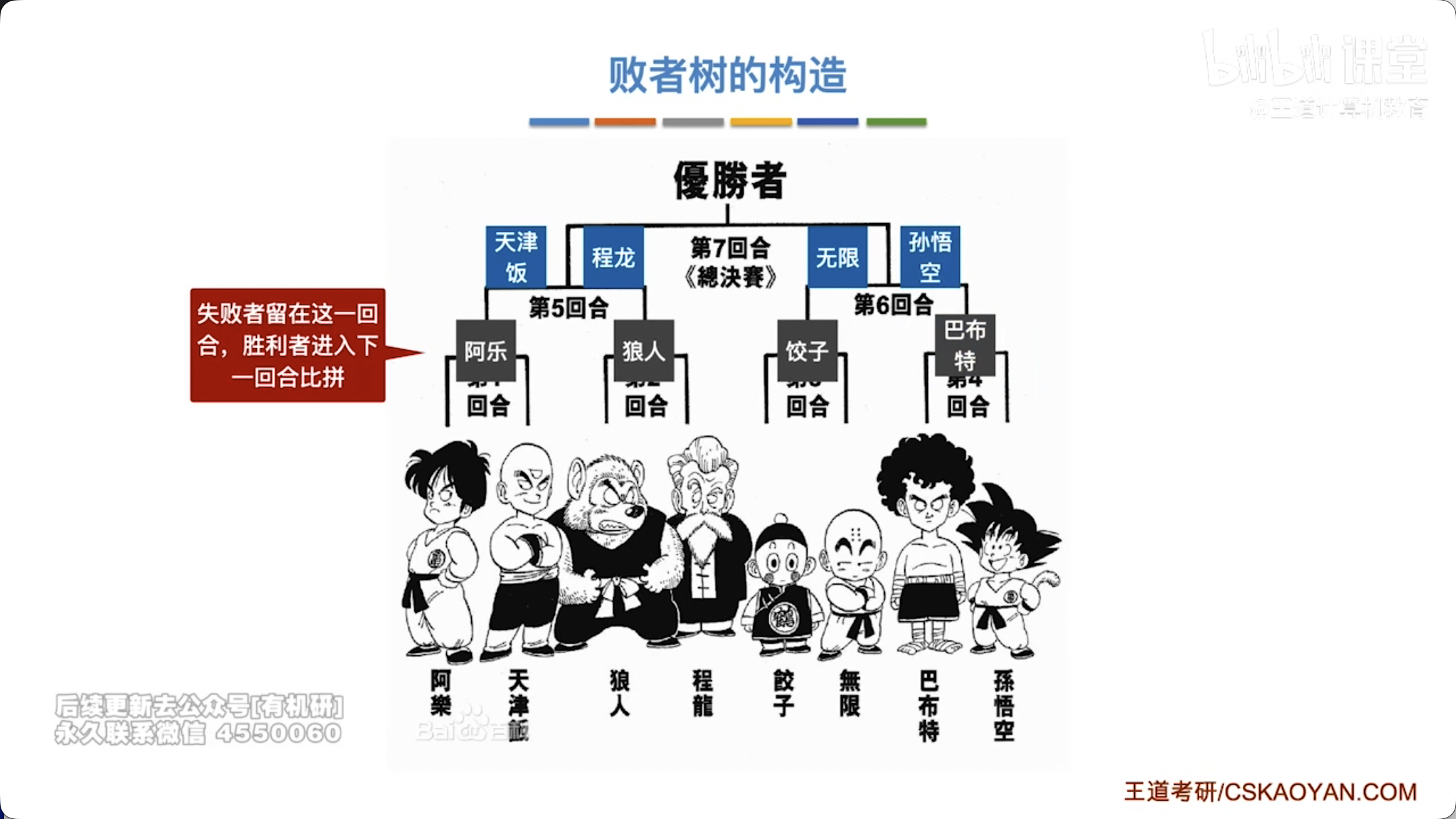
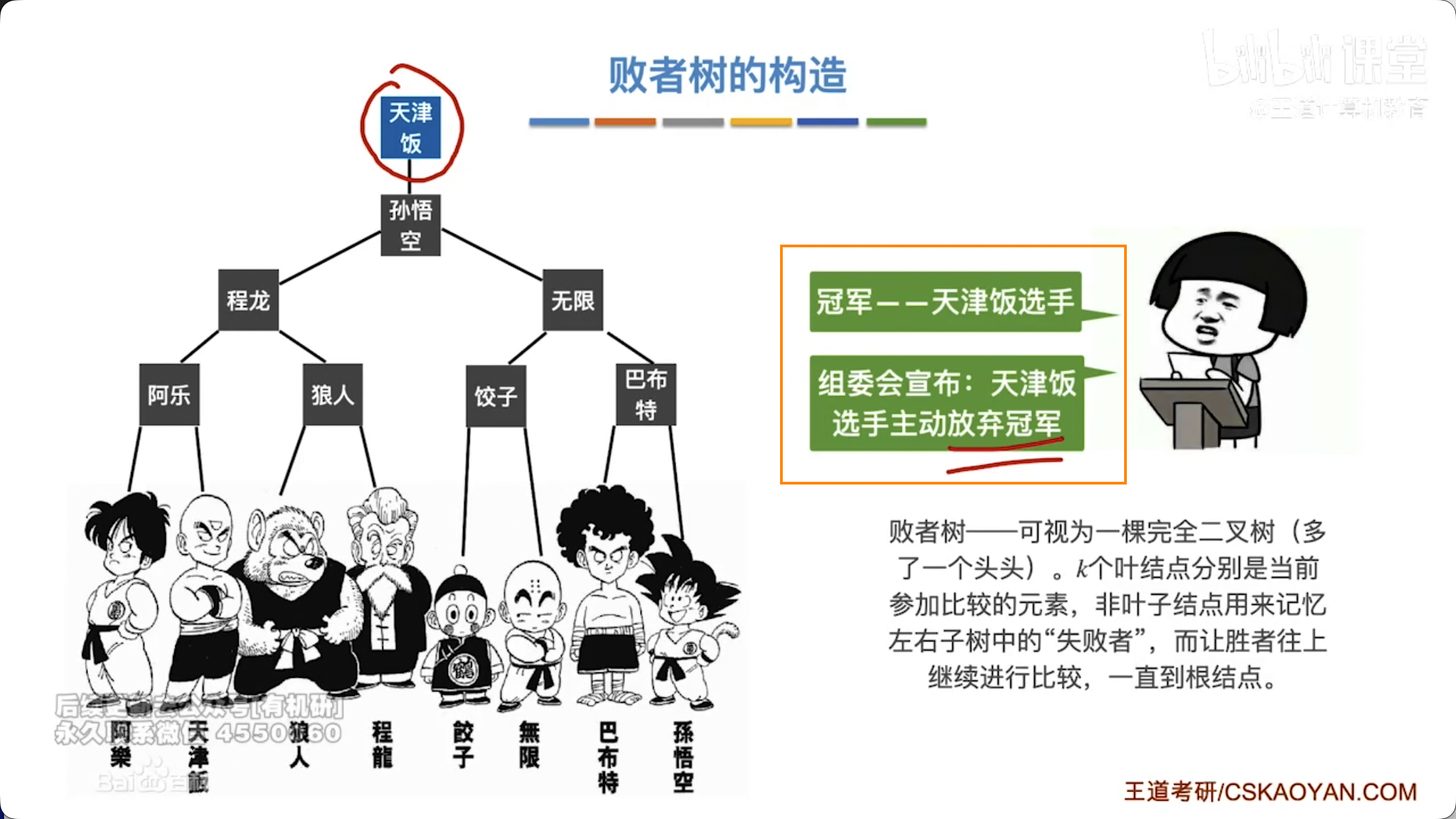
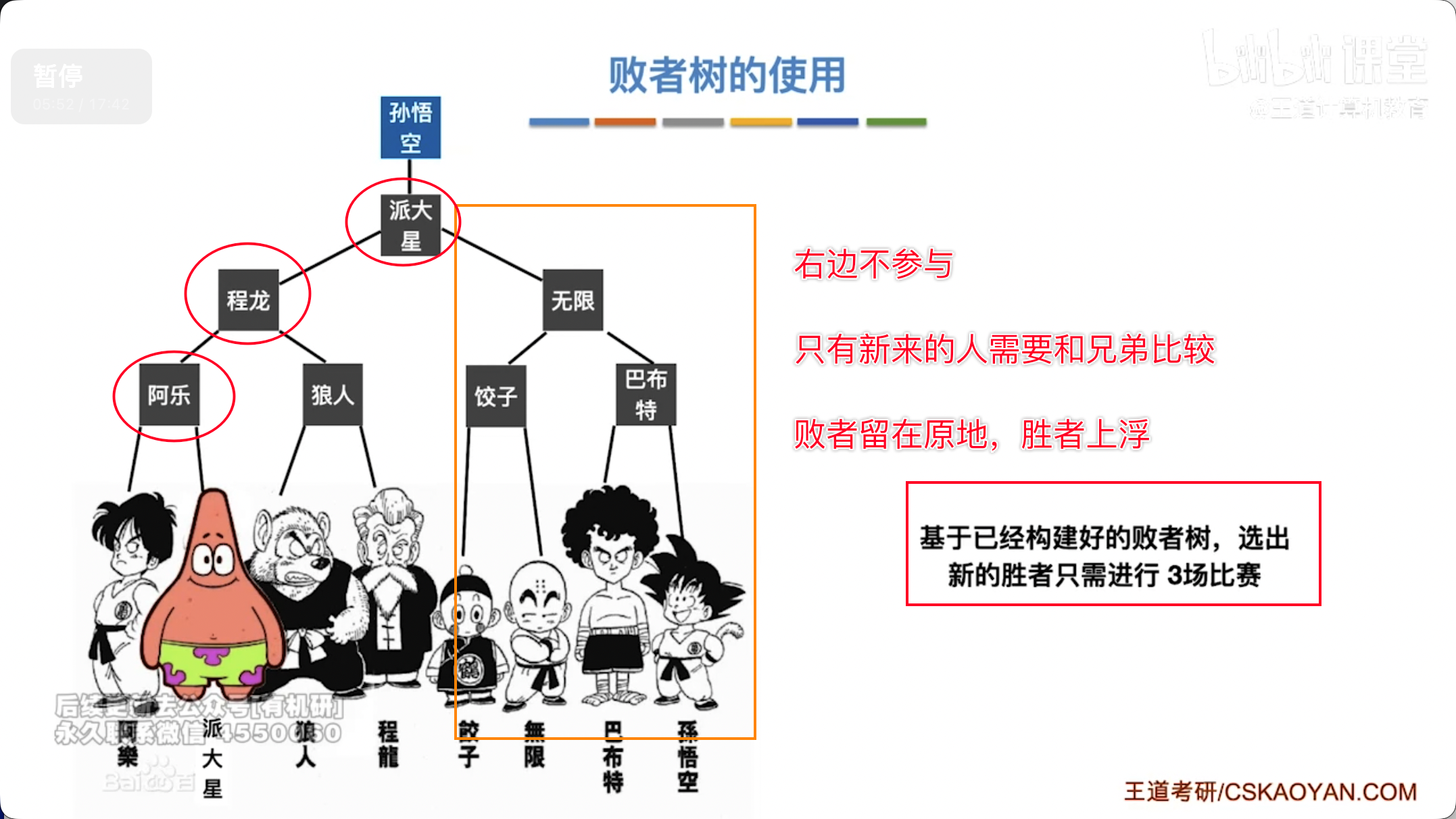
败者树(Loser Tree):
- 概念:一种特殊的完全二叉树,用于在多路归并中快速选择最小元素的数据结构。它能高效地从 个输入缓冲区中选出最小的元素。
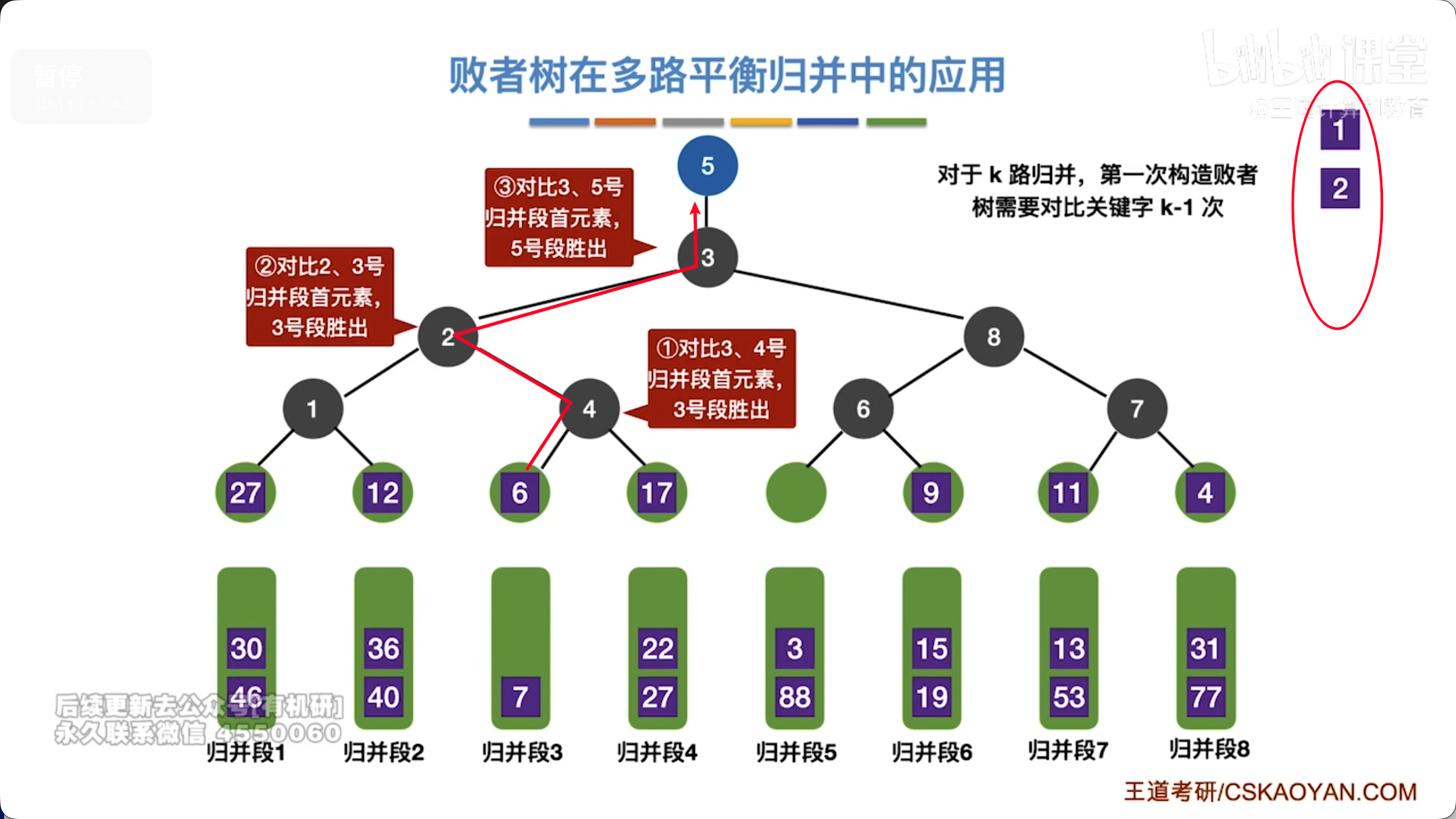
- 例如正常情况下,8 路平衡归并,选出最小值需要对比 7 次 ()
- 使用败者树可以优化到
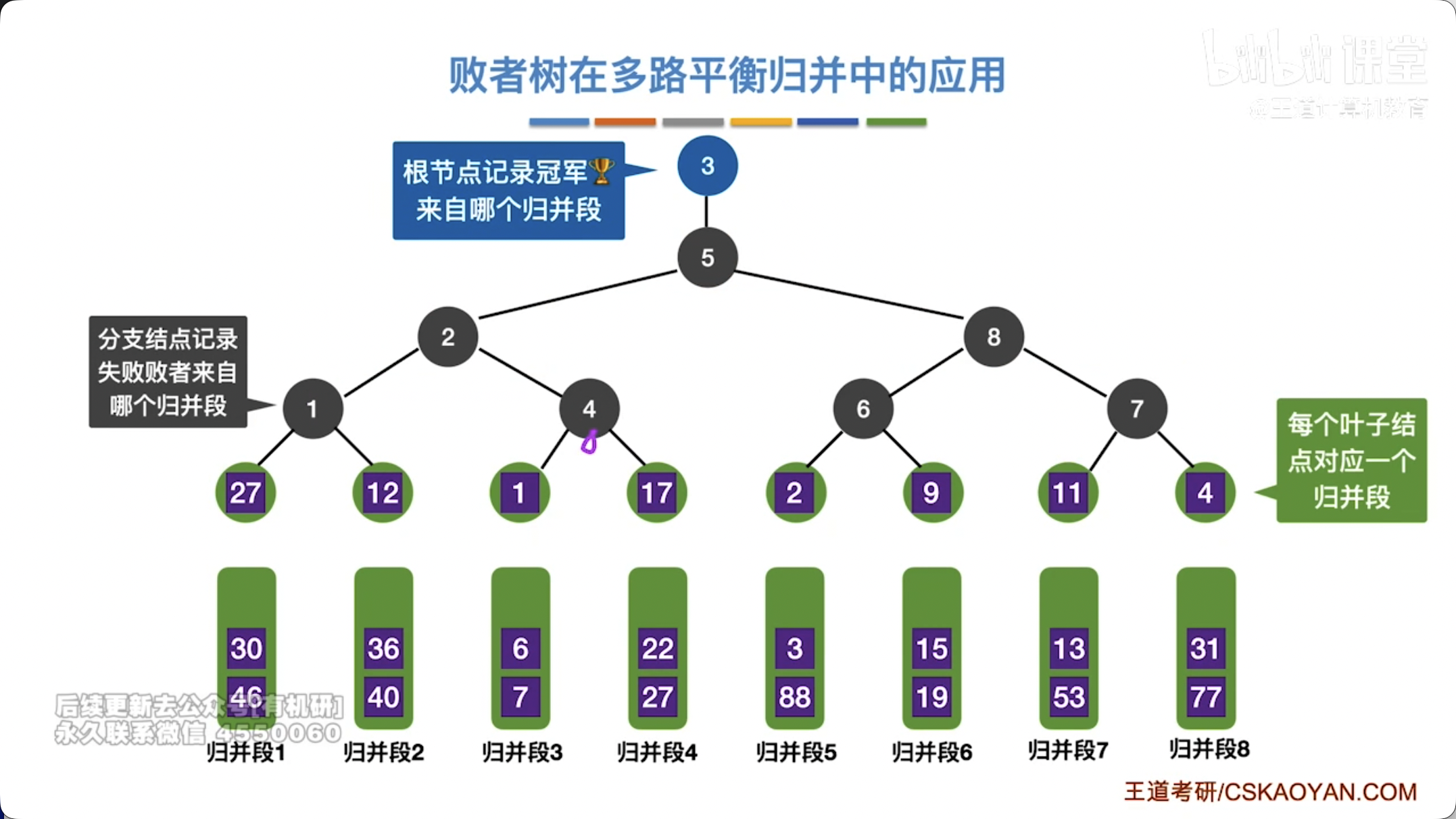
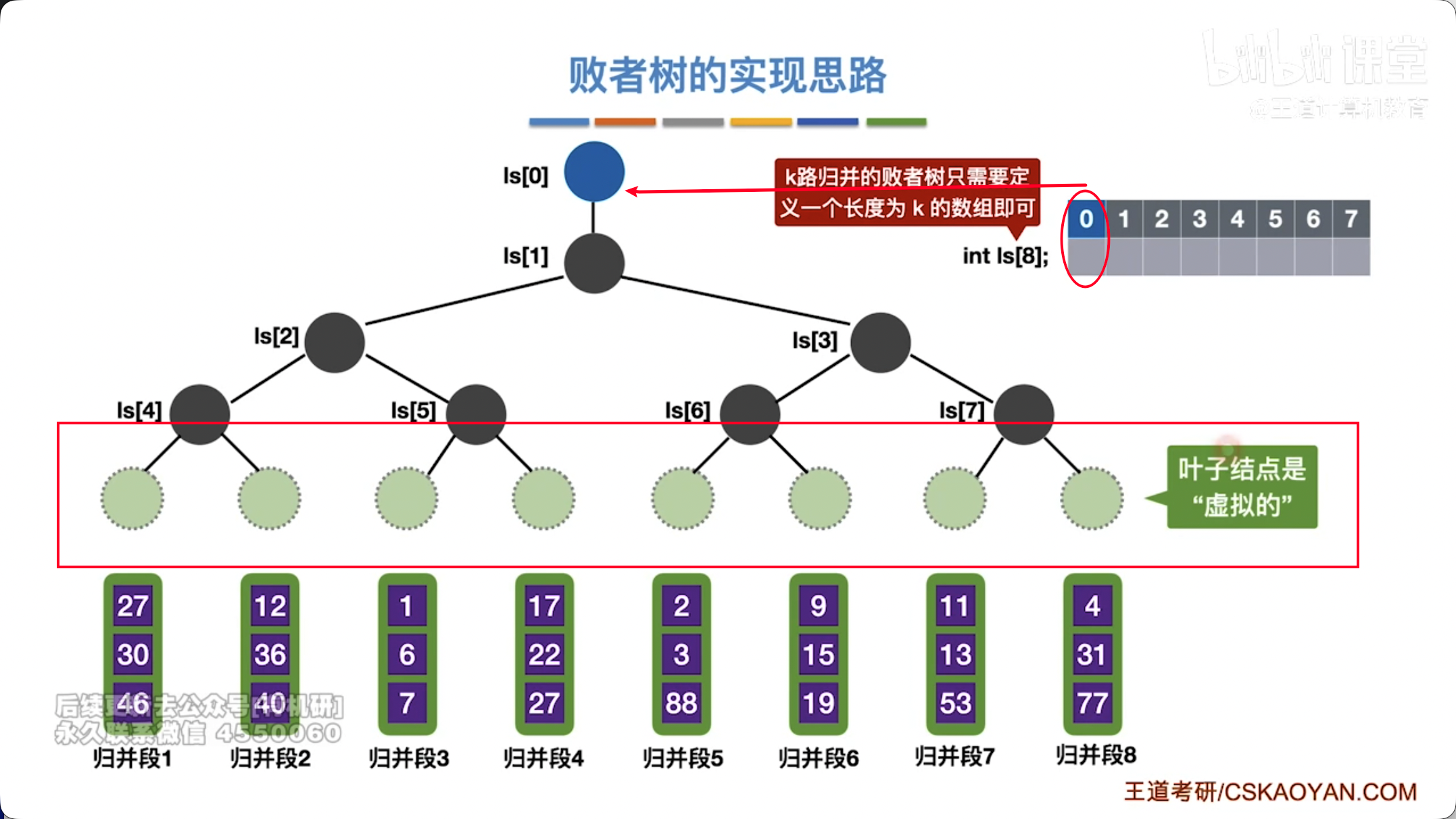
- 结构:
- 叶子节点:表示 个输入归并段的当前待比较元素。
- 非叶子节点:存储其子树中败者的索引(即在比较中被淘汰的那个元素的索引),根节点存储胜者的索引。
- 根节点:胜者树的根节点存储的是最终的胜者,而败者树的根节点存储的是最终的败者,但其父节点(通常是虚构的或通过逻辑处理)会指向最终的胜者。更常见的理解是,败者树的根节点记录了最终的胜者(即所有输入元素中的最小值)的索引,而其他非叶子节点记录了其子节点中比较的败者。
- 工作原理:
- 初始化:将 个输入段的第一个元素作为叶子节点进行两两比较,将败者存入父节点,胜者继续向上比较,直到根节点,根节点记录最终的胜者(最小值)的索引。
- 选择最小元素:根节点所指向的元素即为当前所有输入段中的最小元素。
- 重新调整:将选出的最小元素从其对应的输入缓冲区中移除,并读入该缓冲区中的下一个元素。然后,从该元素所在的叶子节点开始,向上逐层与其“父节点”中存储的败者进行比较。新的胜者继续向上晋级,新的败者存入对应的父节点,直到根节点。这个调整过程只需要沿着一条从叶子到根的路径进行,时间复杂度为 。
- 优点:
- 高效选择:每次选择最小元素只需要 的时间,大大优于 的顺序比较。
- 减少比较次数:总比较次数显著降低。
置换 - 选择排序
生成初始归并段
置换 - 选择排序(Replacement Selection):
- 概念:一种生成更长初始归并段的外部排序方法。它利用内存作为“工作区”,并结合了内部排序和外部归并的思想。
- 原理:
- 内存工作区:在内存中开辟一个固定大小的区域(如 个记录)。
- 填充工作区:从外存输入 个记录到内存工作区。
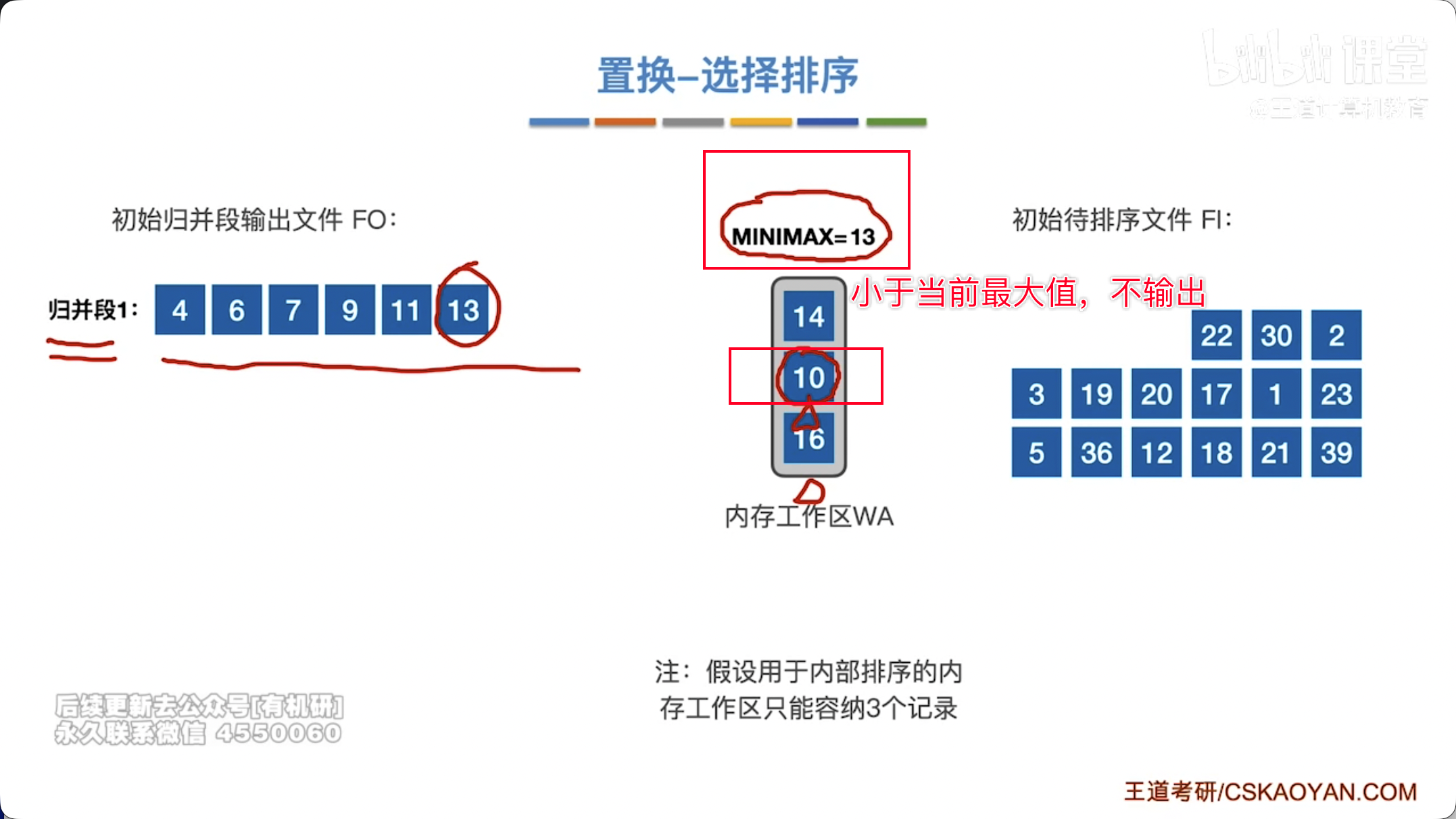
- 选择最小元素:从工作区中选择当前最小的记录作为输出(形成当前归并段的一部分)。
- 替换与比较:
- 若从外存读入的下一个记录大于等于刚刚输出的记录,则将新读入的记录放入工作区中刚才输出记录的位置,继续从工作区中选择最小的输出。
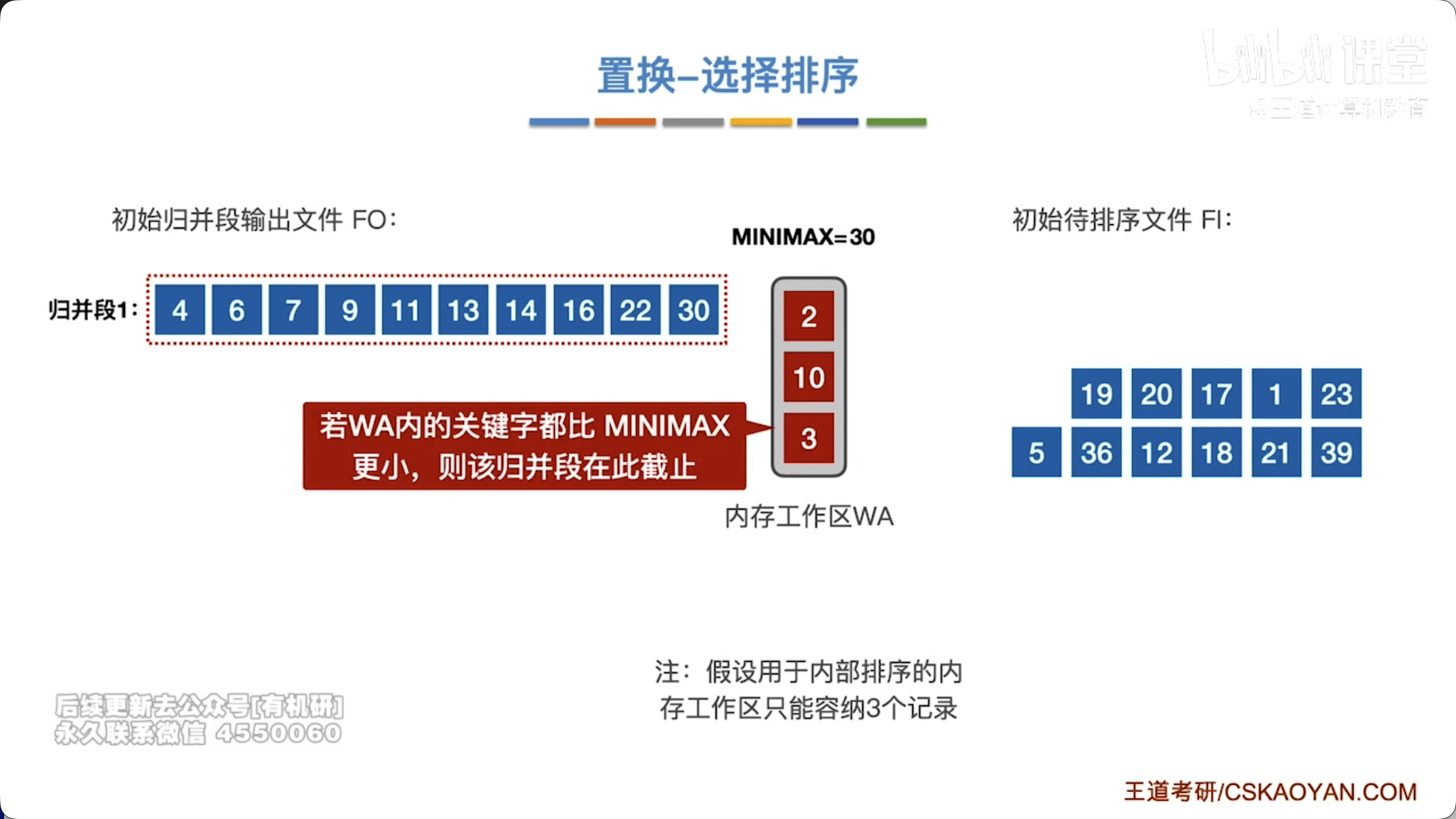
- 若从外存读入的下一个记录小于刚刚输出的记录,则该新记录不能加入当前归并段(因为它比当前已输出的元素小,无法保持有序性)。将该记录标记为“冻结”或“下一归并段的候选”,不参与当前归并段的比较,直到当前归并段结束。通常做法是将其放入一个“等待区”,或者将工作区中该位置标记为“已输出,待填充下一归并段的元素”。
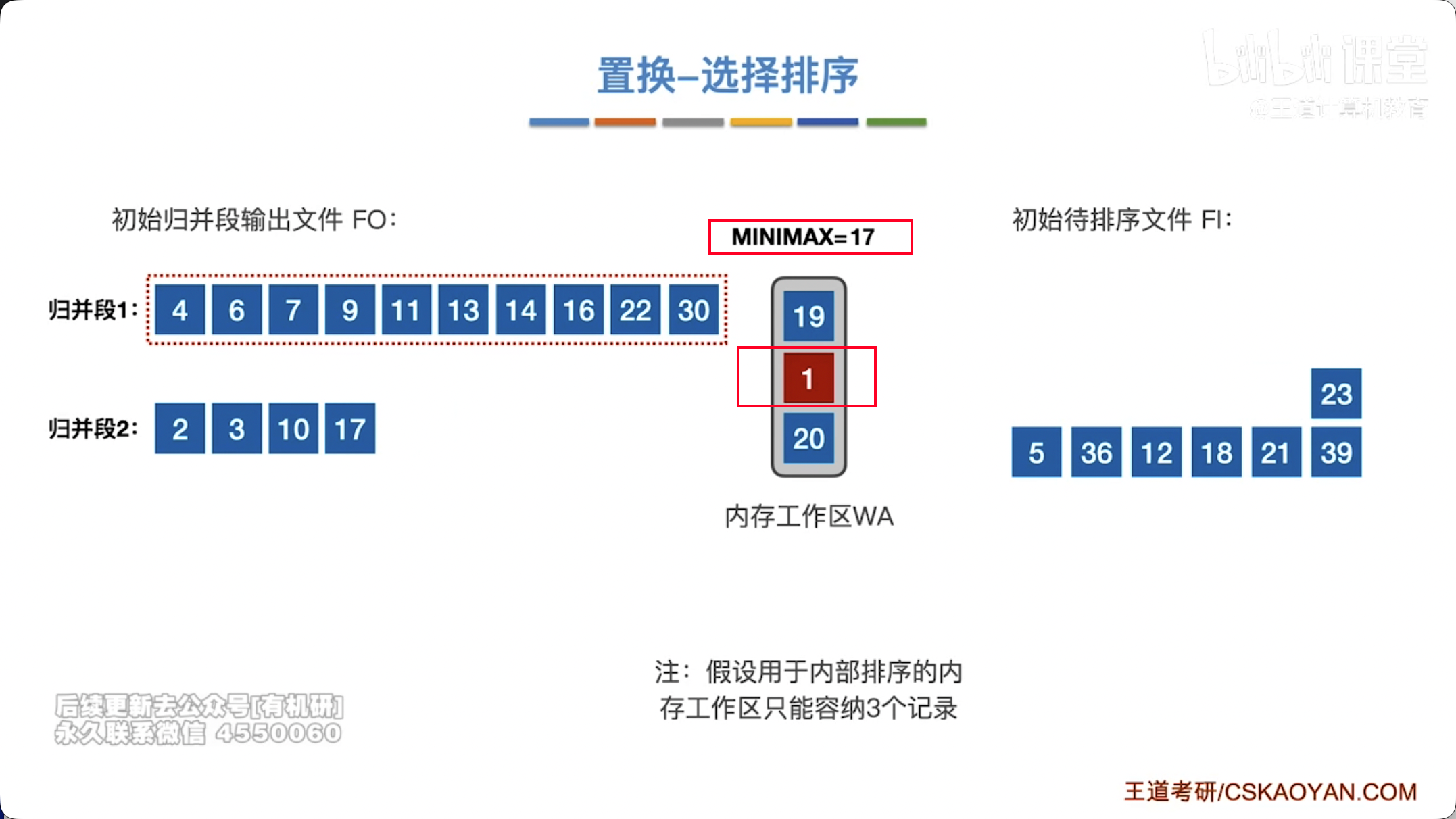
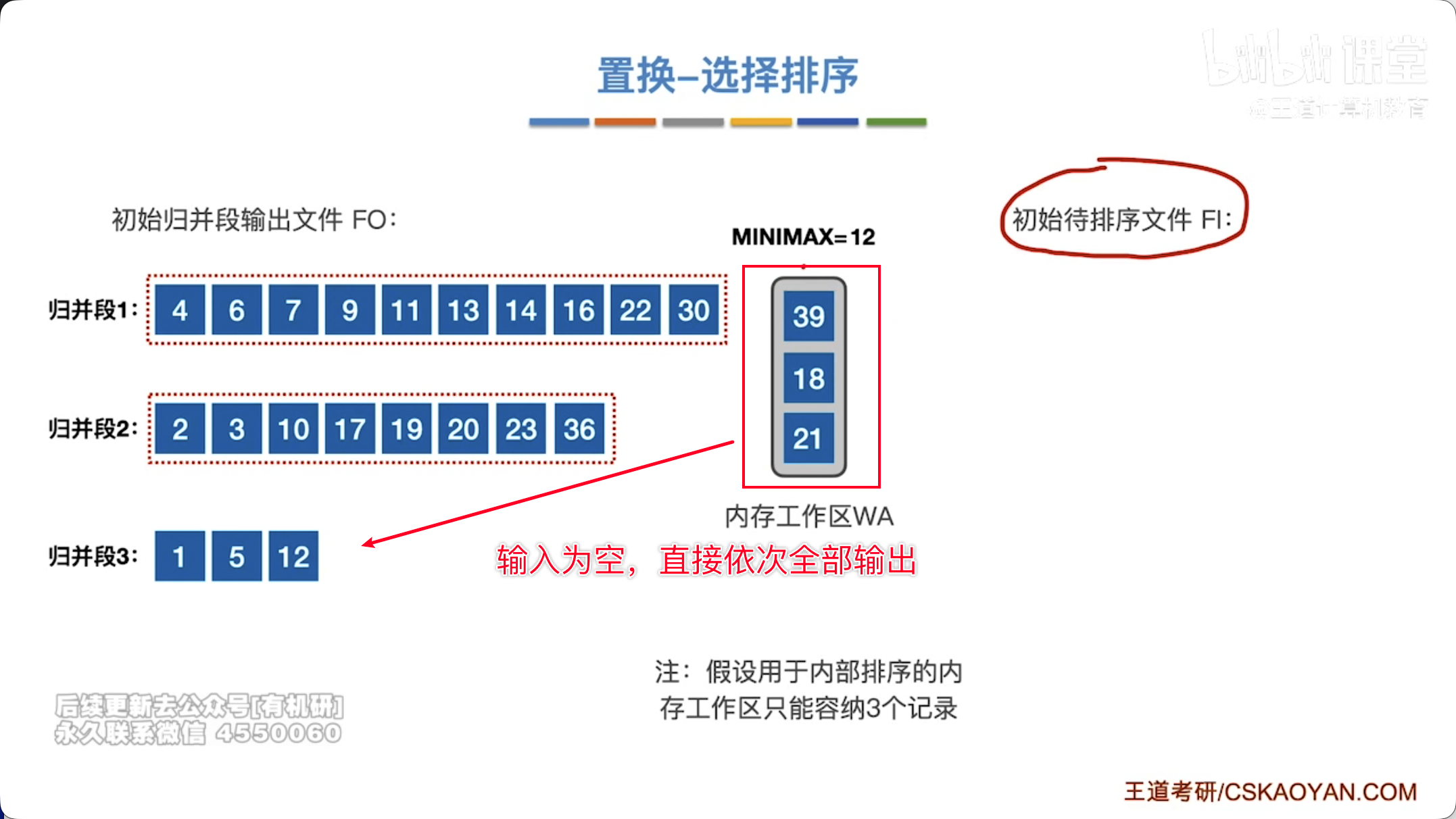
- 循环:重复上述过程,直到内存工作区中所有元素都已输出完毕,或者所有未输出的元素都“冻结”(即小于已输出的最后一个元素)。此时,一个初始归并段生成完毕。
- 生成新的归并段:将“冻结”的元素解冻,作为下一个初始归并段的开始,重复上述过程。
- 优点:
- 生成的初始归并段的平均长度可达到内存工作区大小的两倍(),显著长于简单内部排序生成的 长度。
- 减少了归并趟数,进而减少了总的 I/O 次数。
- 实现细节:通常使用小根堆来维护内存工作区中的元素,快速选择最小元素。
最佳归并树
最佳归并树(Optimal Merge Tree / Huffman Tree):
- 概念:在多路归并中,当初始归并段的长度不相等时,为了最小化总的 I/O 次数(或总的比较次数),需要构建一种特殊的归并树。
- 构建原理:类似于哈夫曼树的构建过程。
- 将每个初始归并段看作一个叶子节点,其“权值”为该归并段的记录数量。
- 每次选择当前权值最小的 个节点(若不足 个,则用虚拟节点补齐)进行合并,生成一个新的父节点,其权值为所有子节点的权值之和(代表归并后新段的记录数量)。
- 将新生成的父节点放回节点集合中,重复步骤 2,直到只剩下一个根节点。
- 目标:最小化“带权路径长度之和”,即 ,其中 是第 个初始归并段到根节点的路径长度(代表该段参与归并的次数), 是该归并段的长度(或记录数)。这等价于最小化总的 I/O 操作次数。
- 特点:
- 权值小的节点离根节点更远(参与归并次数更多),但其数据量小。
- 权值大的节点离根节点更近(参与归并次数更少),且其数据量大。
- 这种策略确保了总的 I/O 代价最小。
- 适用场景:当初始归并段的长度不一致时,构建最佳归并树才能达到最优性能。若初始归并段长度大致相等,则平衡归并即可。
添加虚段的数量
注意:对于 k 路归并,若初始归并段的数量无法构成一棵严格 k 叉树,则需要补充若干个长度为 0 的“虚段”,再进行 k 叉哈夫曼树的构造。
k 路最佳归并树一定是一棵严格 k 叉树,即树中只包含度为 k(内部结点)和度为 0(叶子结点)的结点。
设度为 k 的结点有 个,度为 0 的结点有 个,归并树总结点数 则:
- 基本关系式:
- 总结点数:
- 树中边数:从度的角度看为 ;从结点数的角度看为 。
- 因此,
- 核心推导:
- 由 移项可得:
n_0 = (k-1)n_k + 1
- 此公式表明,在一棵严格k叉树中,叶子结点数 $n_0$ 和度为k的内部结点数 $n_k$ 满足该关系。 - 为了使 $n_k$(即归并次数)为整数,$(n_0 - 1)$ **必须能被 $(k-1)$ 整除**。即 $(n_0 - 1) \pmod{k-1} = 0$。 #### 虚段数量计算规则 设初始归并段数量为 $r$。我们需要添加 $x$ 个虚段,使得叶子结点总数 $n_0 = r+x$ 满足 $(n_0 - 1) \pmod{k-1} = 0$ 的条件。 1. **若 (初始归并段数量 $r - 1) \pmod{k-1} = 0$** - **说明**: 初始状态已满足构成严格k叉树的条件。 - **结论**: 此时不需要添加虚段,即添加数量为 **0**。 2. **若 (初始归并段数量 $r - 1) \pmod{k-1} = u$ 且 $u \neq 0$** - **说明**: 初始状态不满足条件,需要补充 $x$ 个虚段才能构成严格k叉树。目标是使新的叶子总数 $n_0 = r+x$ 满足 $((r+x)-1) \pmod{k-1} = 0$。 - **推导**: 该条件等价于 $( (r-1) + x ) \pmod{k-1} = 0$,即 $(u+x) \pmod{k-1} = 0$。 - **结论**: 为使添加的虚段最少,应取 $x$ 使 $u+x$ 成为 $k-1$ 的最小倍数(即 $k-1$ 本身),故需要补充的虚段数量为 $x = (k-1) - u$。 ### 举例说明 ![[attachment/a30b53da4962f221f47bccc1c84007da_MD5.png|磁盘IO次数等于WPL✖️2]] ![[attachment/87a880099d31b22ac18367a5039a2883_MD5.png]] ![[attachment/d8389be0fff92c1b7e95a73741e2e53f_MD5.png]] ![[attachment/3b4d8dd73cc0d9731700b412268bcff0_MD5.png]] - 如果最终的结点不是 3 的倍数,那么需要加入**虚段**来保证最终是 3 个结点 ![[attachment/9c51cf793f01a3a06ad63934f1bfc1a1_MD5.png|❌错误例子]] ![[attachment/13c3a9d91210a3fbcb514e0d356eccdf_MD5.png|✅正确做法]] ![[attachment/ea14f98f05c5a012aa9099e7bcfead9a_MD5.png]]