平衡二叉树
定义
平衡二叉树 (Balanced Binary Tree) 是一种特殊的二叉排序树,其核心目的是通过在插入和删除结点时进行调整,来避免二叉排序树退化成线性链表,从而保证查找、插入、删除等操作的时间复杂度维持在 。
AVL 树是最早被提出的自平衡二叉搜索树,其定义如下:
- 它首先是一棵二叉排序树。
- 对于树中的任意结点,其左子树和右子树的高度差的绝对值不超过 1。
平衡因子 (Balance Factor, BF):结点的左子树高度减去其右子树高度,即 。
- 在 AVL 树中,所有结点的平衡因子的取值只可能是 -1, 0, 1。
- 一旦某个结点的 ,则该树失去平衡,需要进行旋转调整。
插入
AVL 树的插入操作分为两步:
- 查找并插入:首先按照二叉排序树的规则,找到新结点的插入位置并将其作为叶子结点插入。
- 回溯与调整:从新插入结点的父结点开始,沿路径向上回溯至根结点,依次检查每个结点的平衡因子。如果发现某个结点的平衡因子绝对值变为 2,说明以该结点为根的子树失去平衡,需要进行旋转操作。
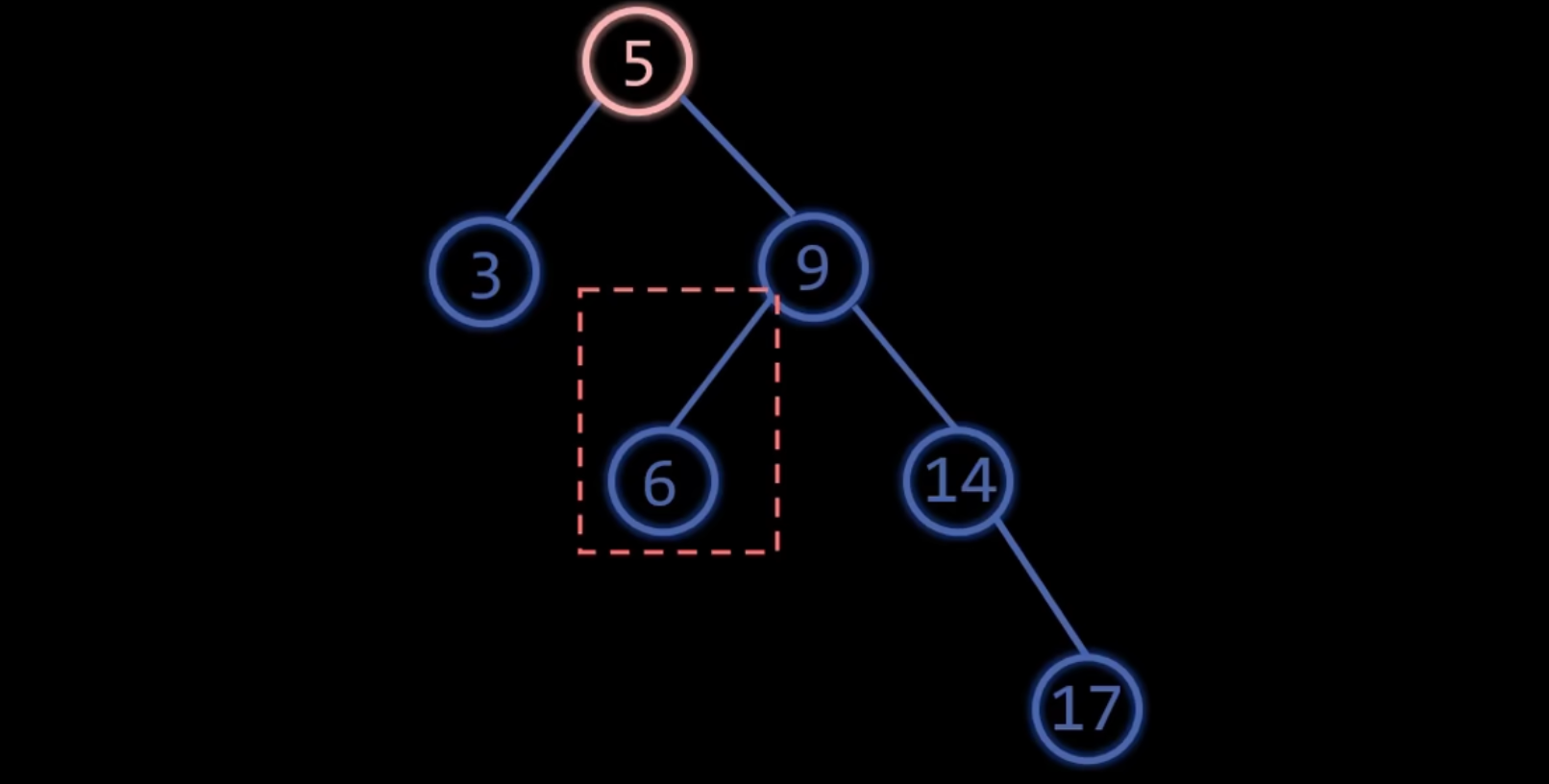
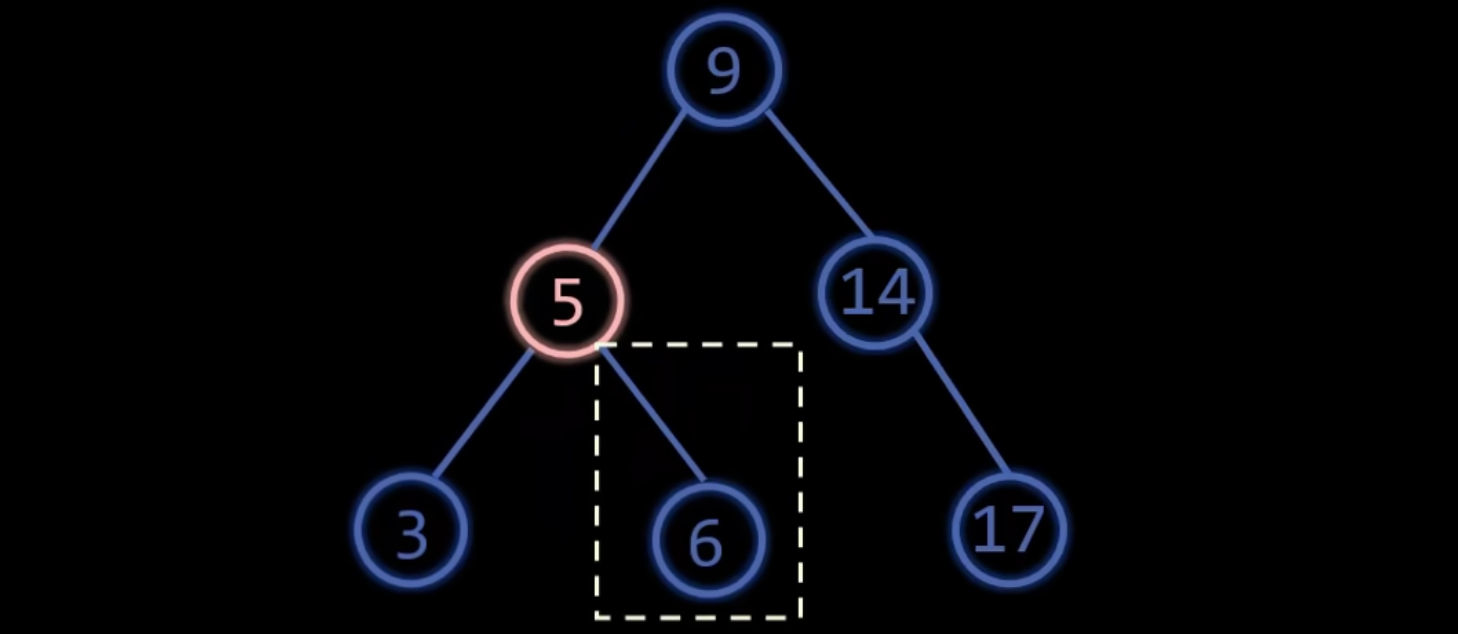
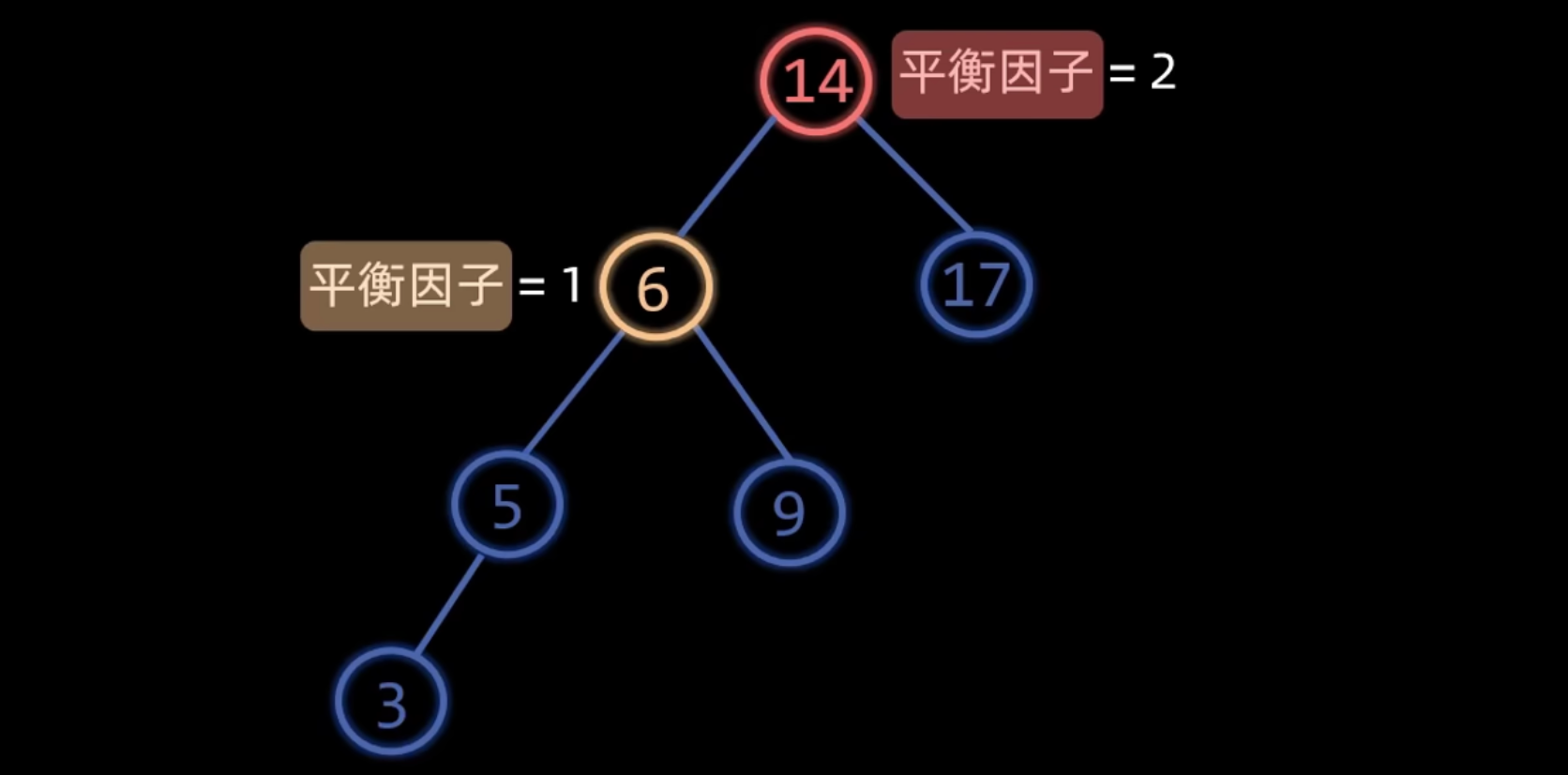
最小不平衡子树
最小不平衡子树是指在插入或删除操作后,以离插入/删除结点最近的那个平衡因子绝对值大于 1 的结点为根的子树。对该子树进行调整,即可使整个树重新恢复平衡。
设这个最近的失衡结点为 A,调整主要针对 A 以及其子孙结点。
左旋
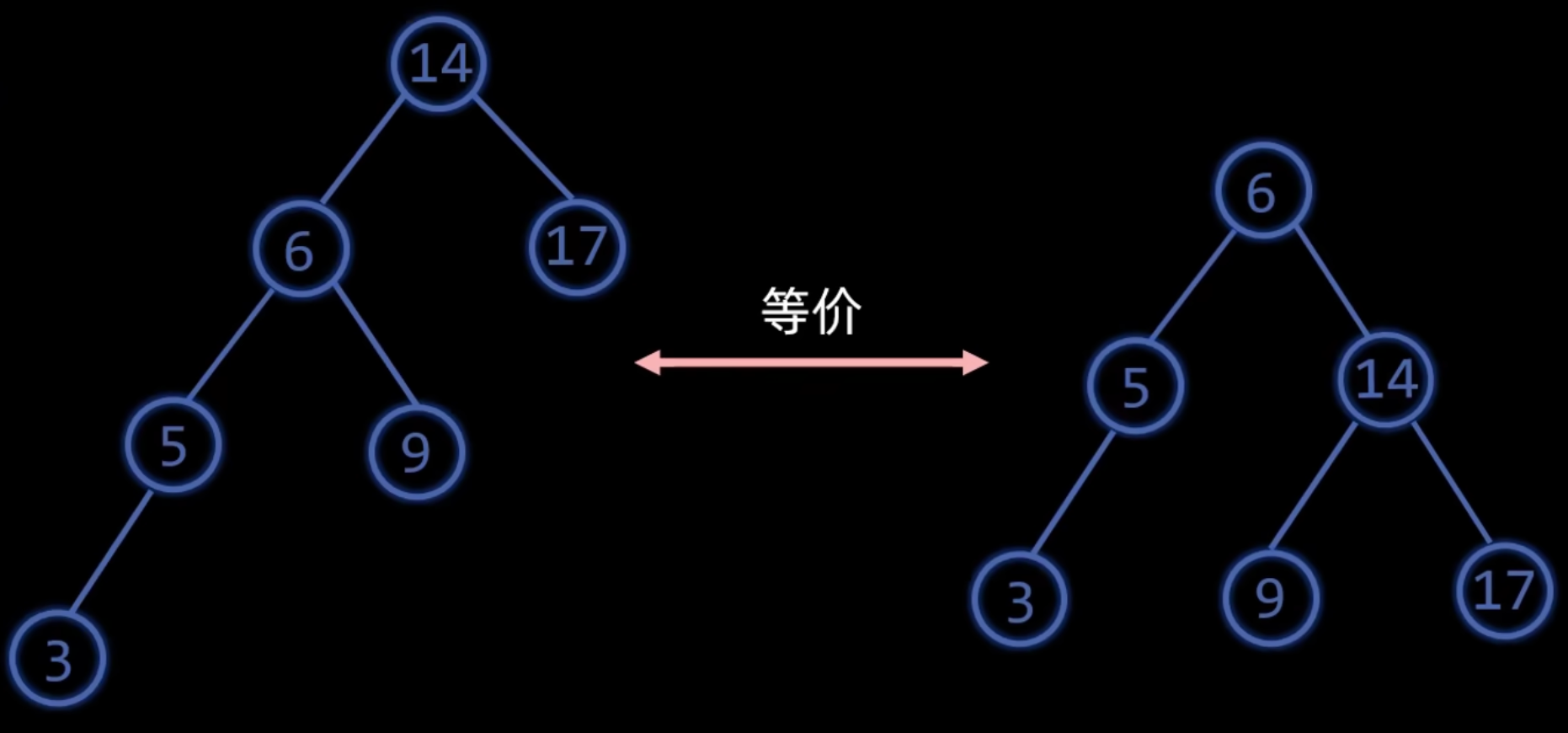
旋转不改变中序遍历结果
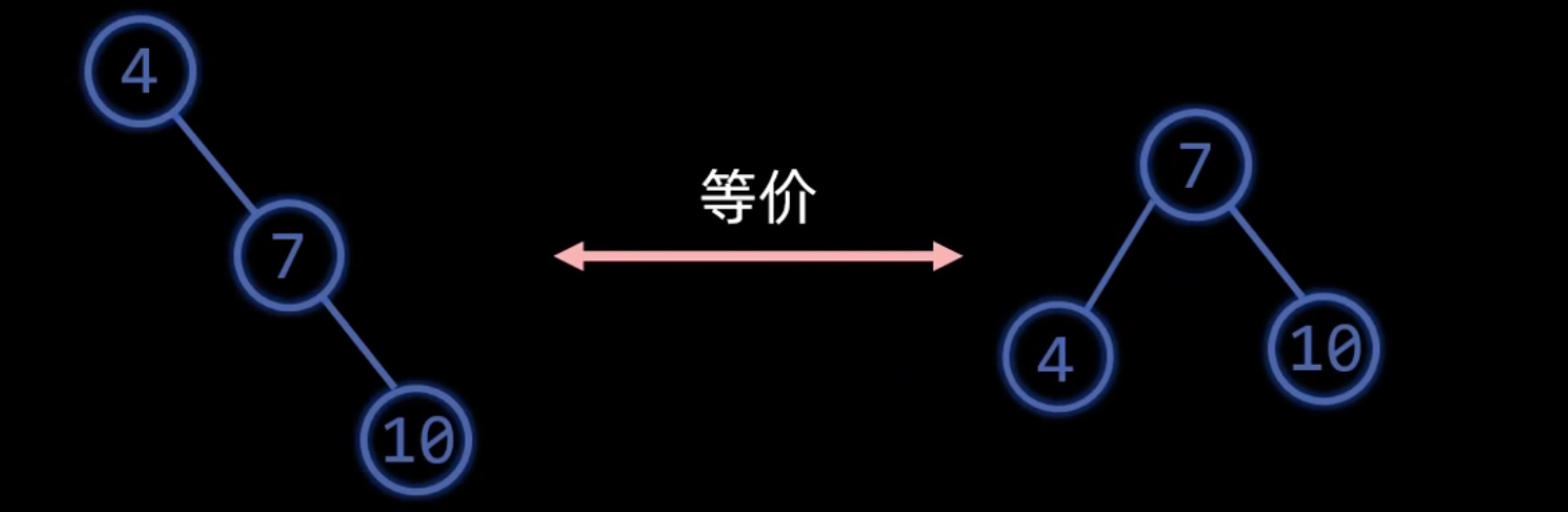
冲突的左孩变右孩
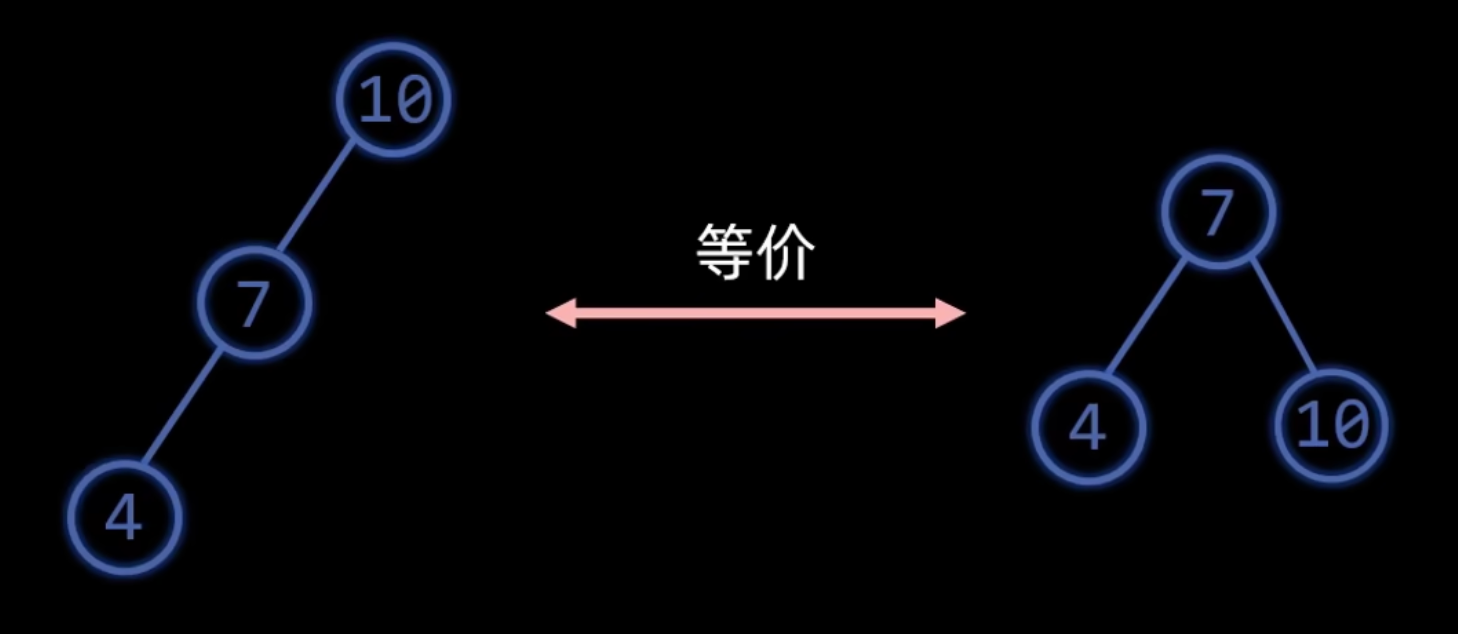
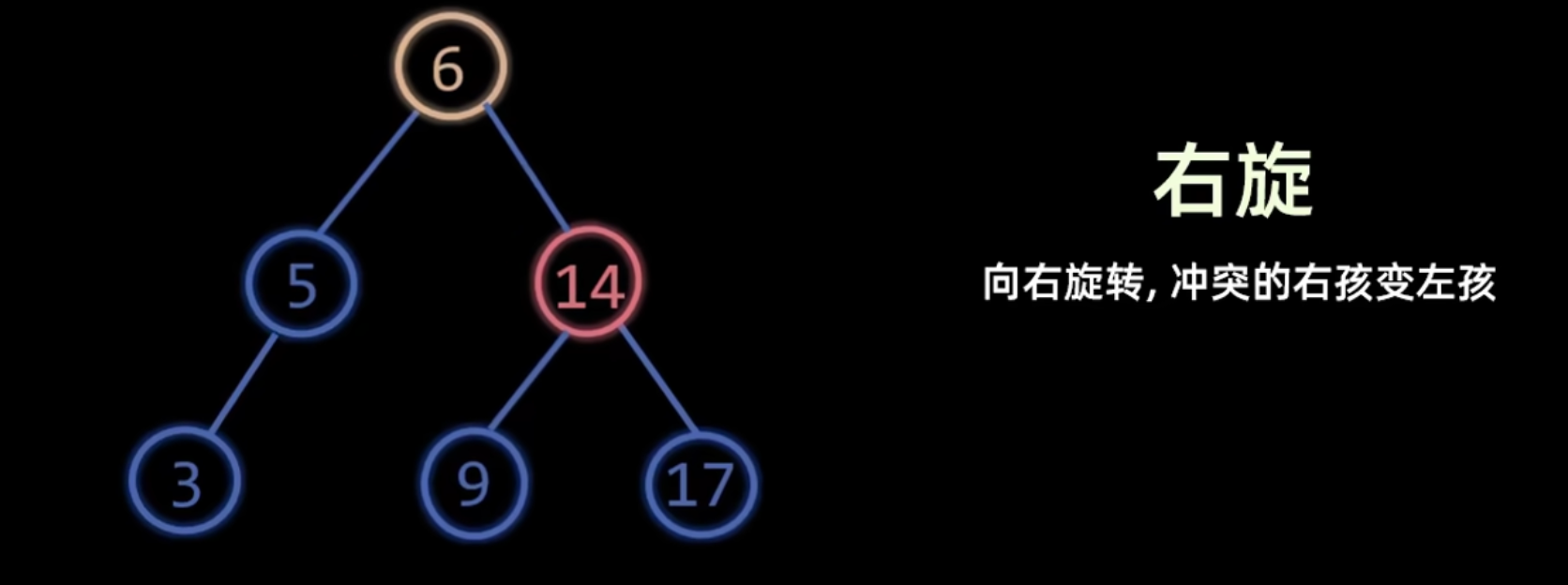
右旋
同样冲突的右孩变左孩
LL 平衡旋转
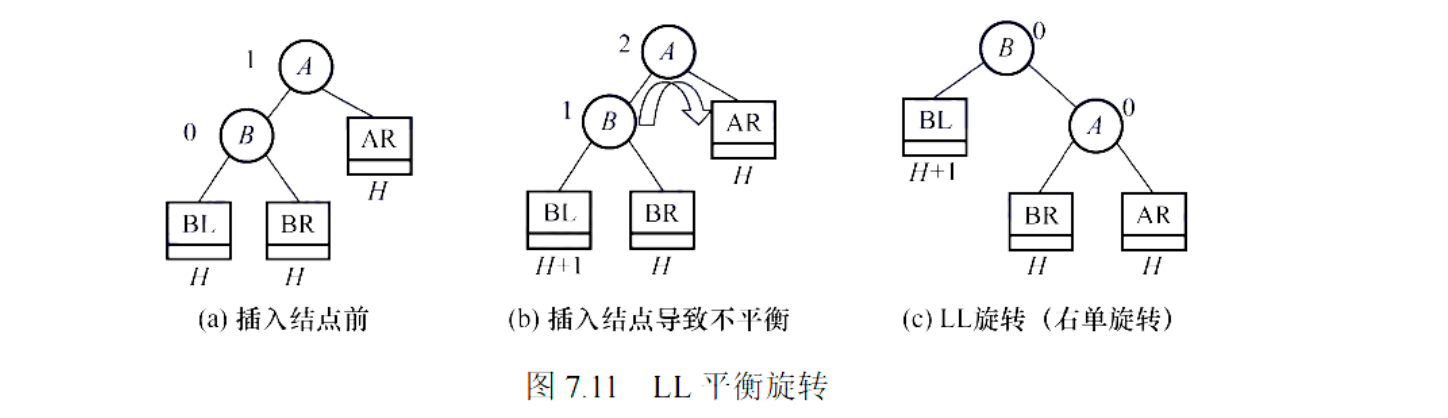
- 成因:在新结点插入到
A的左孩子的左子树上,导致A的平衡因子变为 2。 - 调整方法:对
A进行一次右旋 (Right Rotation)。- 以
A的左孩子B为新的根。 A成为B的右孩子。B原来的右子树成为A的新左子树。
- 以
RR 平衡旋转
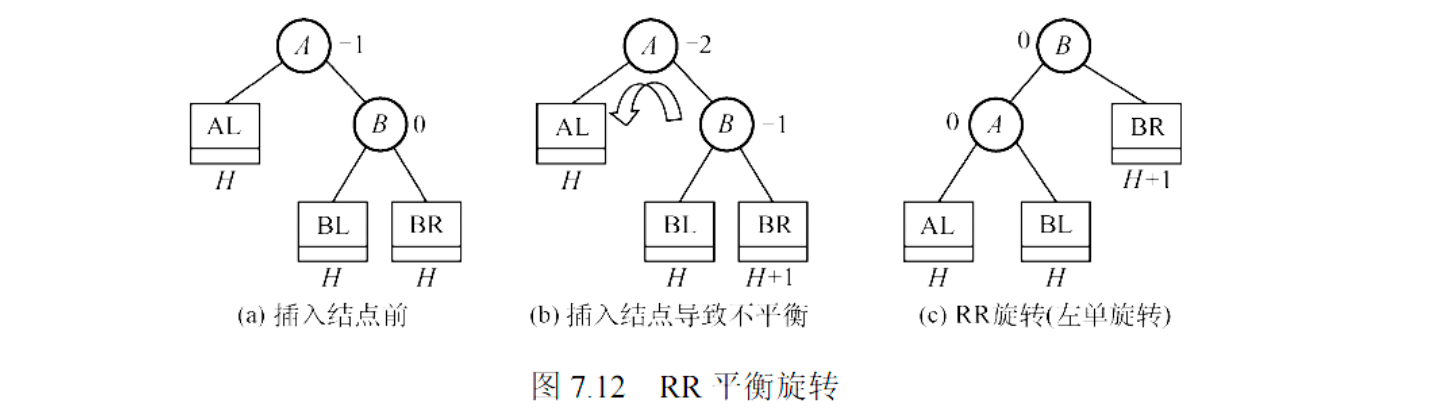
- 成因:在新结点插入到
A的右孩子的右子树上,导致A的平衡因子变为 -2。 - 调整方法:对
A进行一次左旋 (Left Rotation)。- 以
A的右孩子B为新的根。 A成为B的左孩子。B原来的左子树成为A的新右子树。
- 以
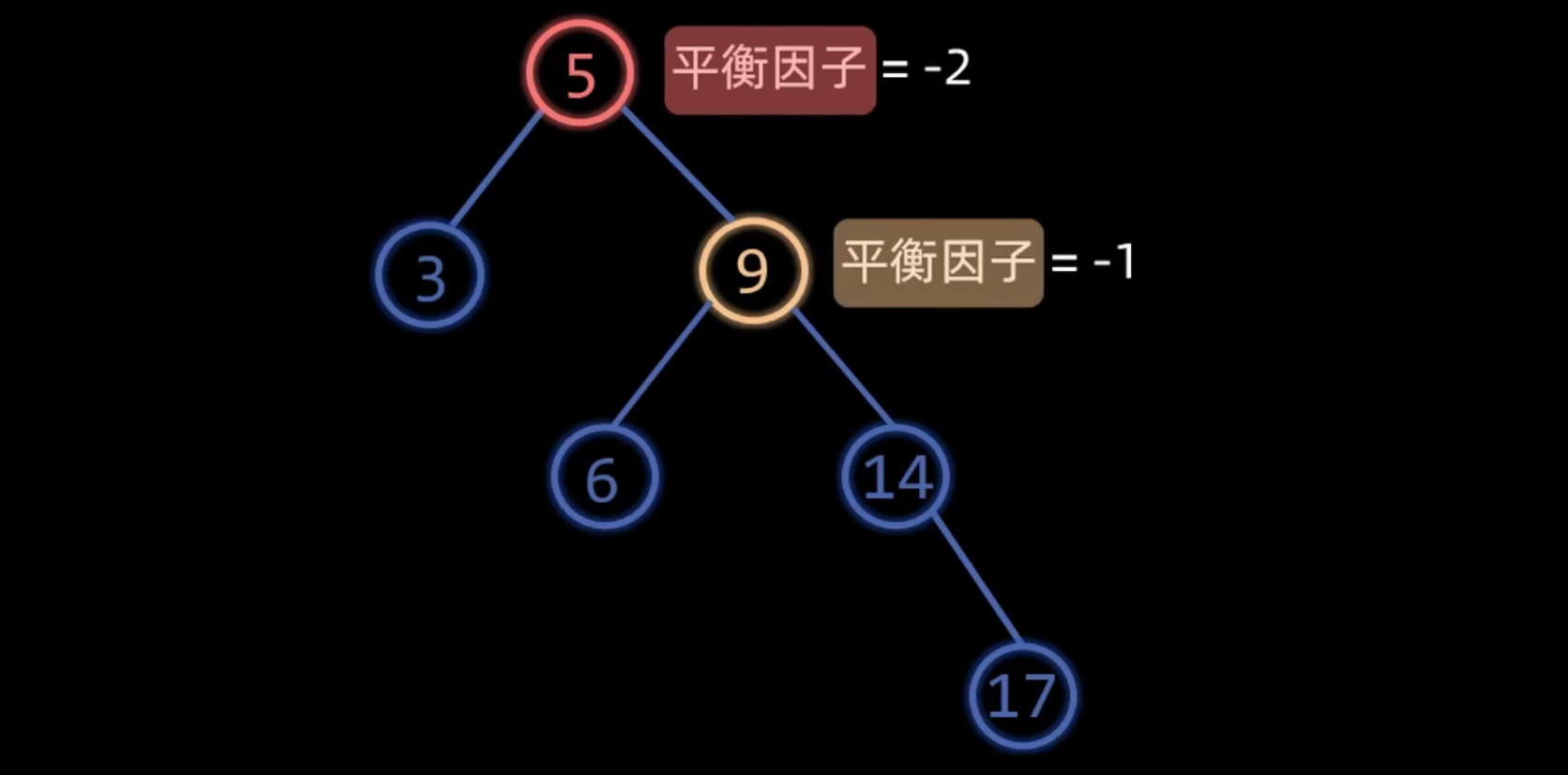
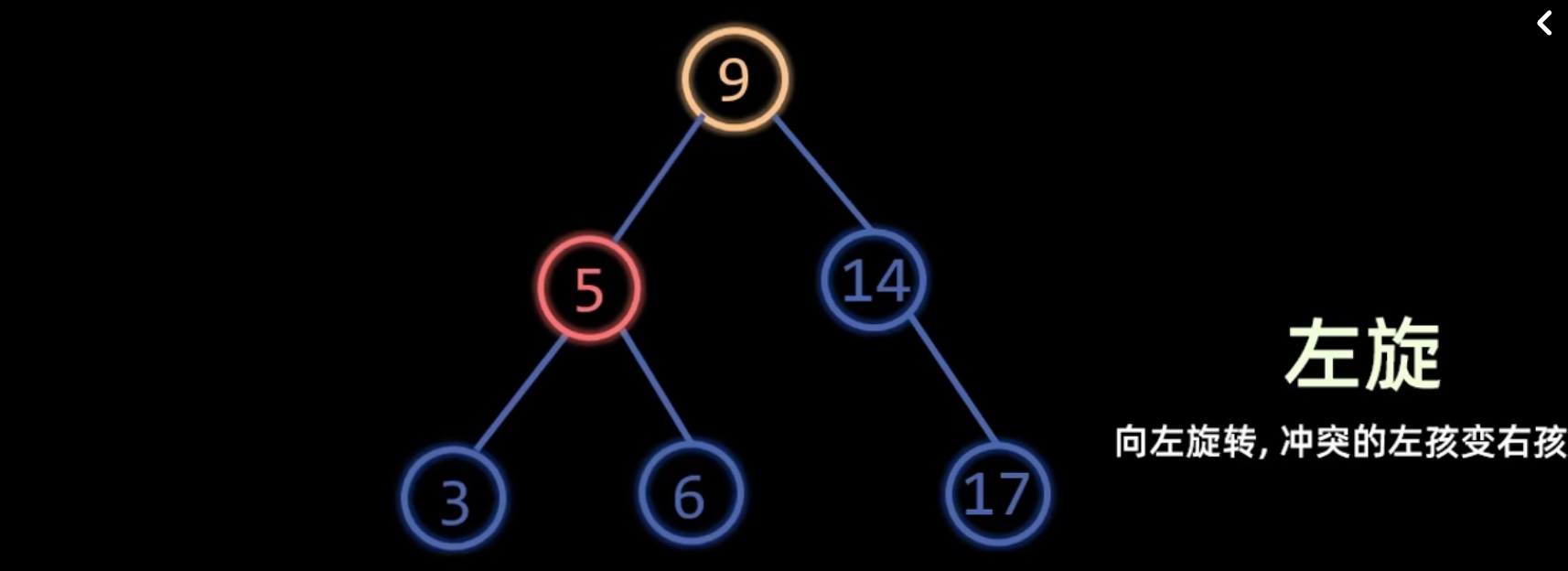
LR 平衡旋转
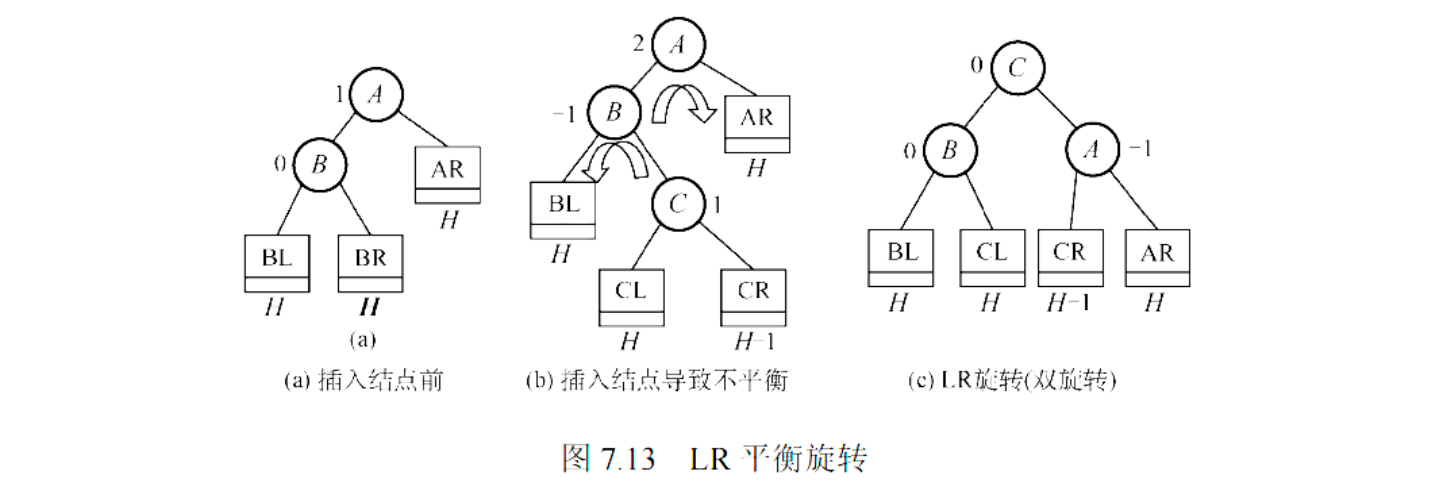
- 成因:在新结点插入到
A的左孩子的右子树上,导致A的平衡因子变为 2。 - 调整方法:进行双旋 (Double Rotation),先左后右。
- 先左旋:对
A的左孩子B进行一次左旋。 - 再右旋:对
A本身进行一次右旋。
- 先左旋:对
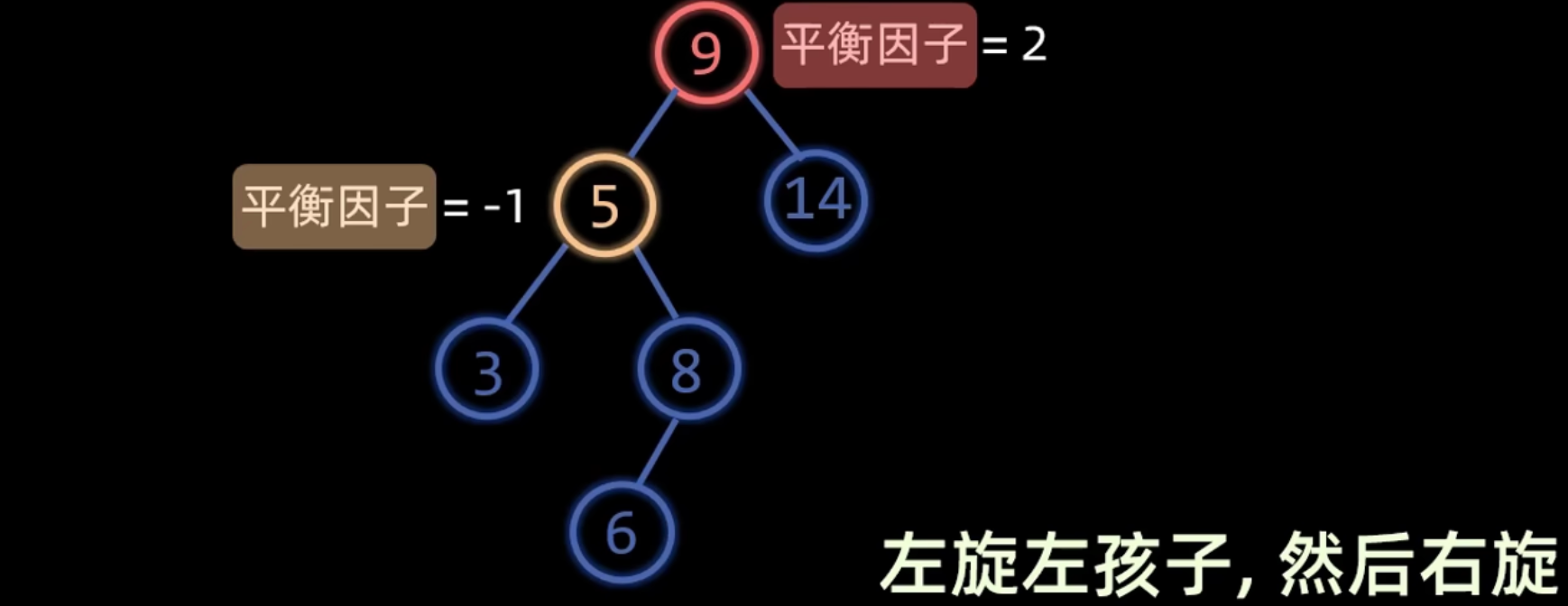
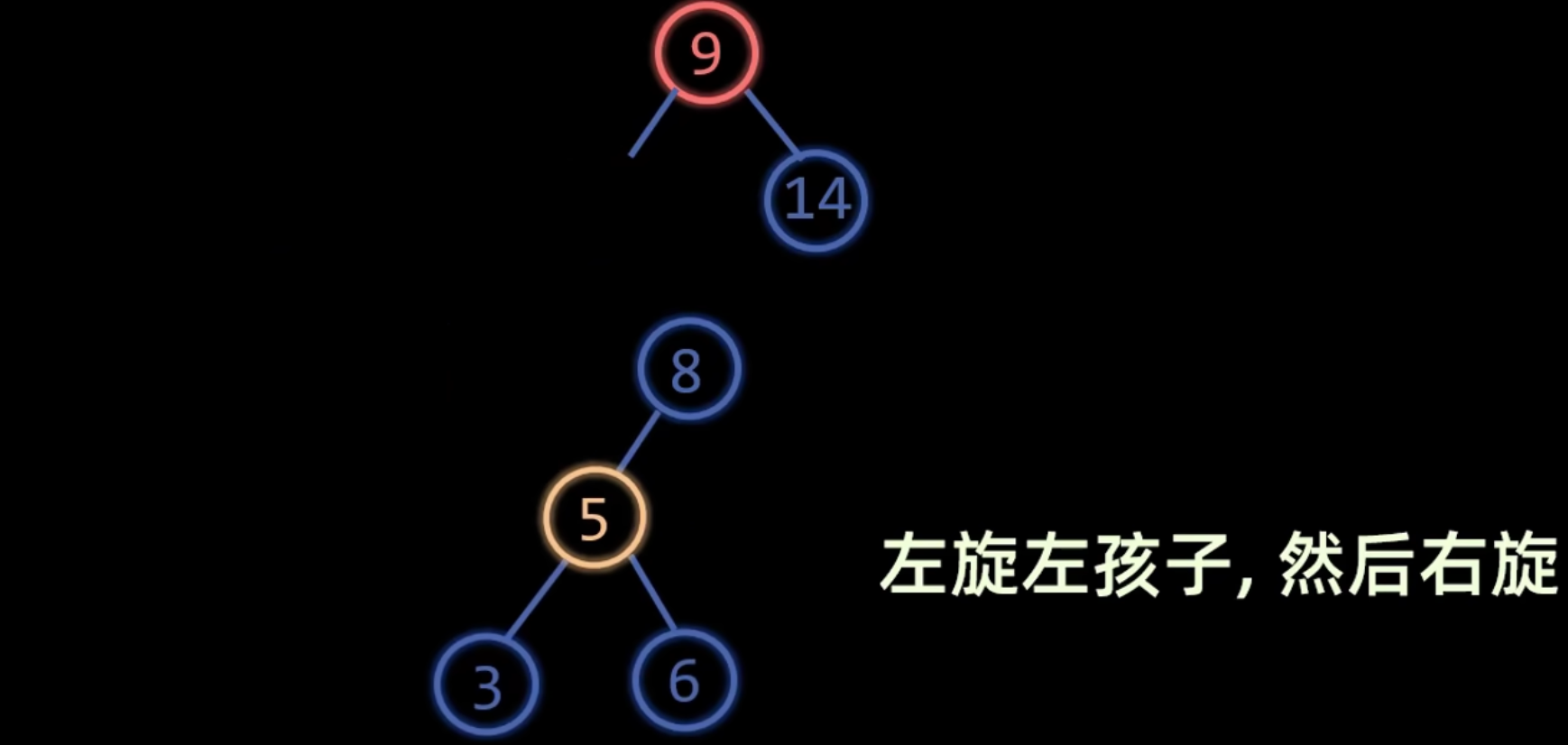
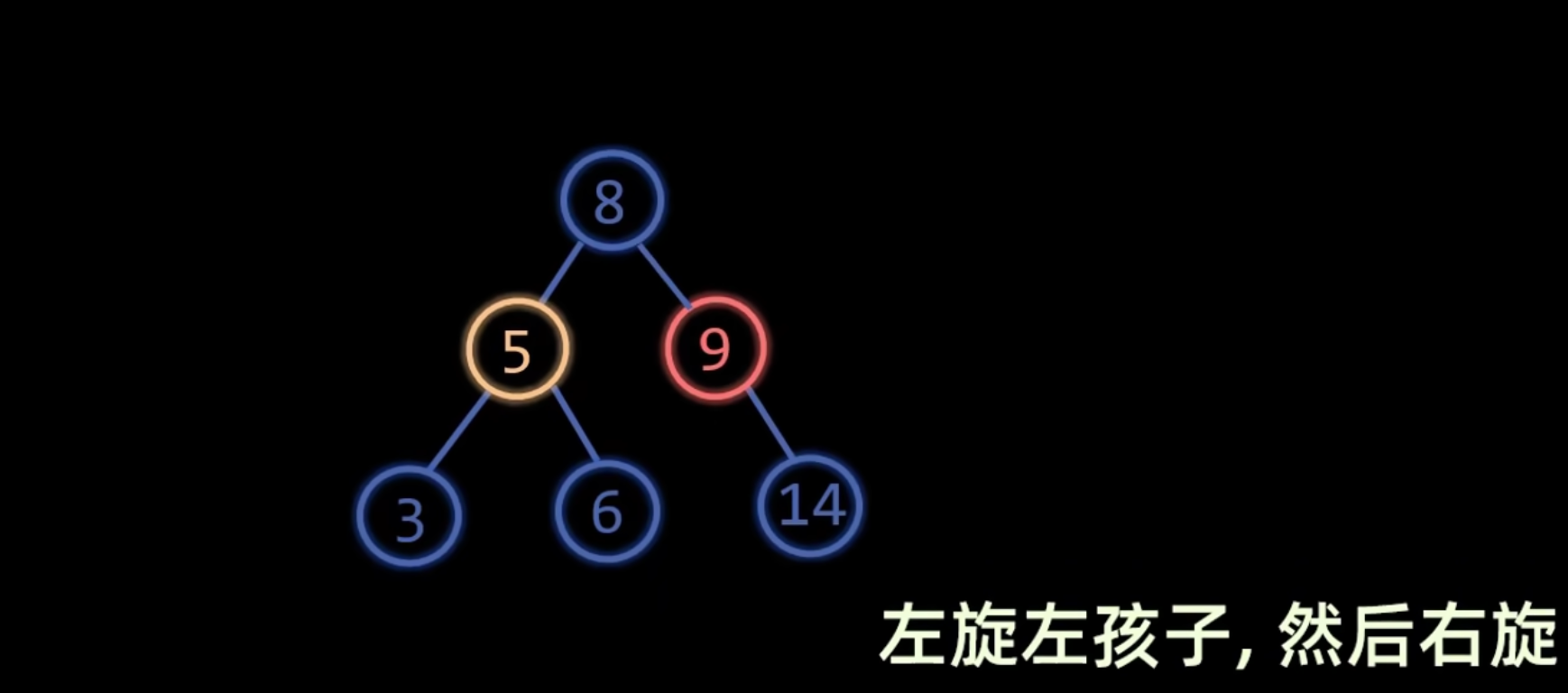
RL 平衡旋转
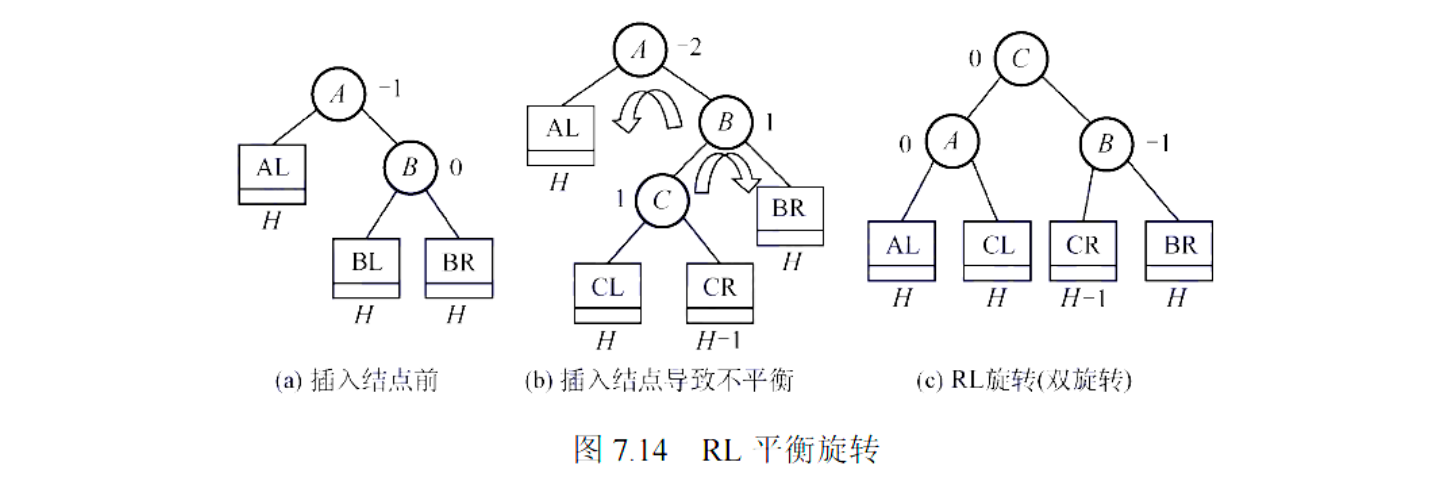
- 成因:在新结点插入到
A的右孩子的左子树上,导致A的平衡因子变为 -2。 - 调整方法:进行双旋 (Double Rotation),先右后左。
- 先右旋:对
A的右孩子B进行一次右旋。 - 再左旋:对
A本身进行一次左旋。
- 先右旋:对
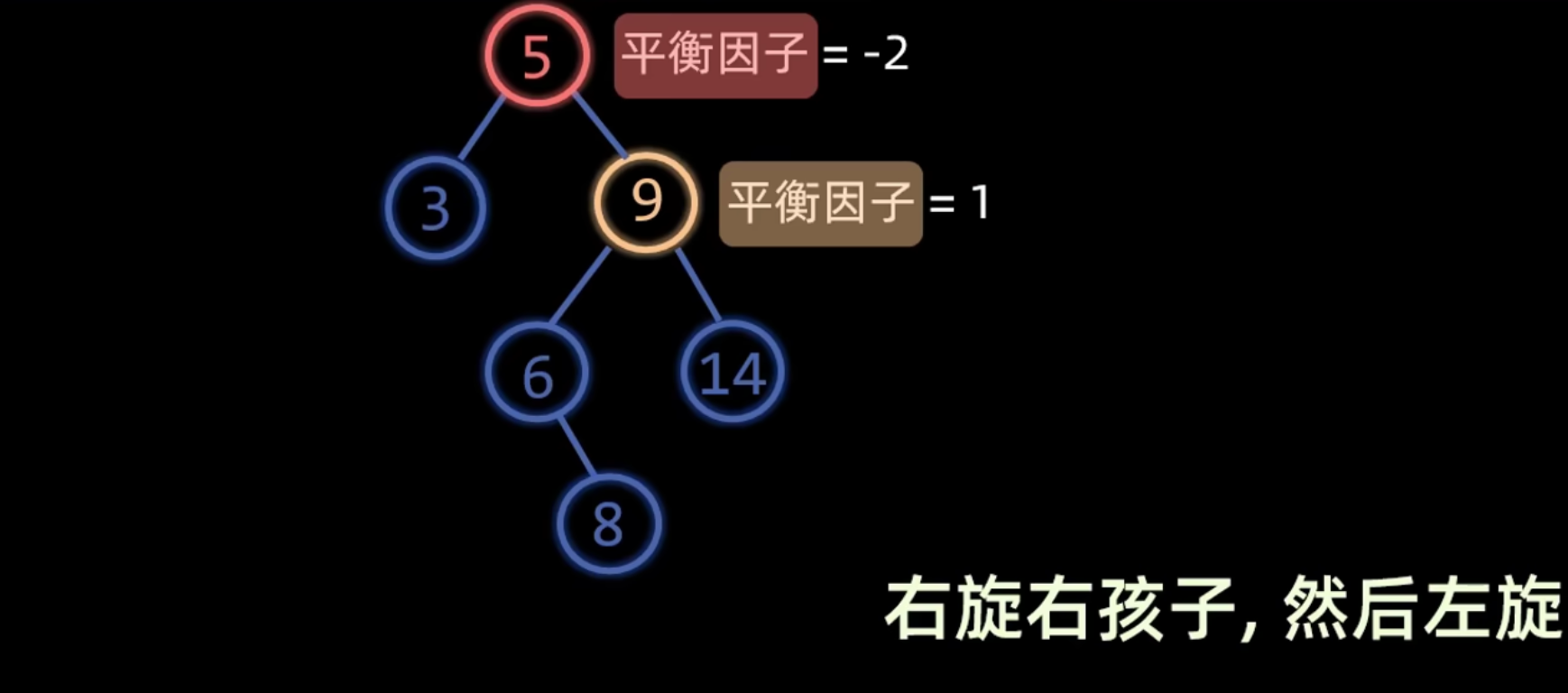
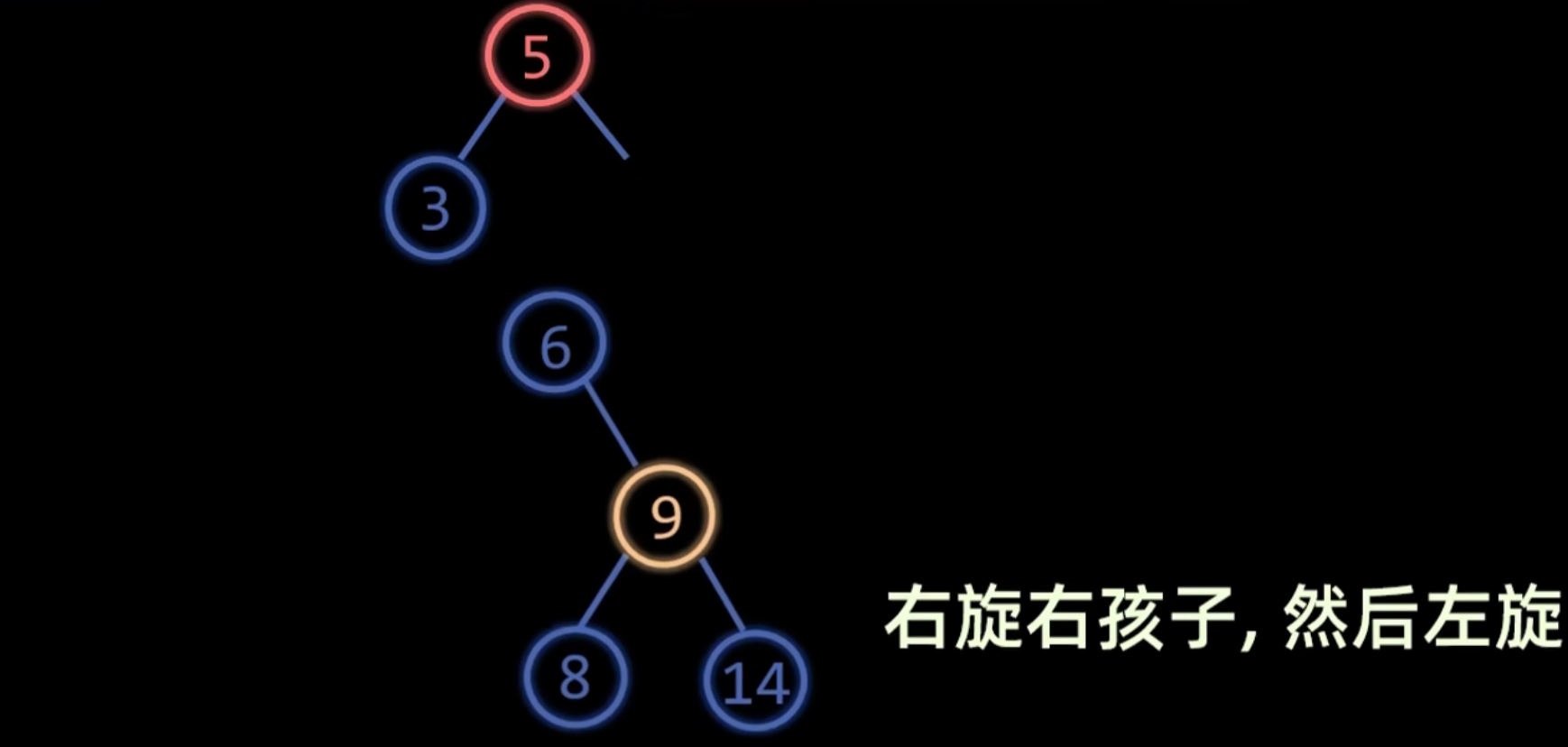
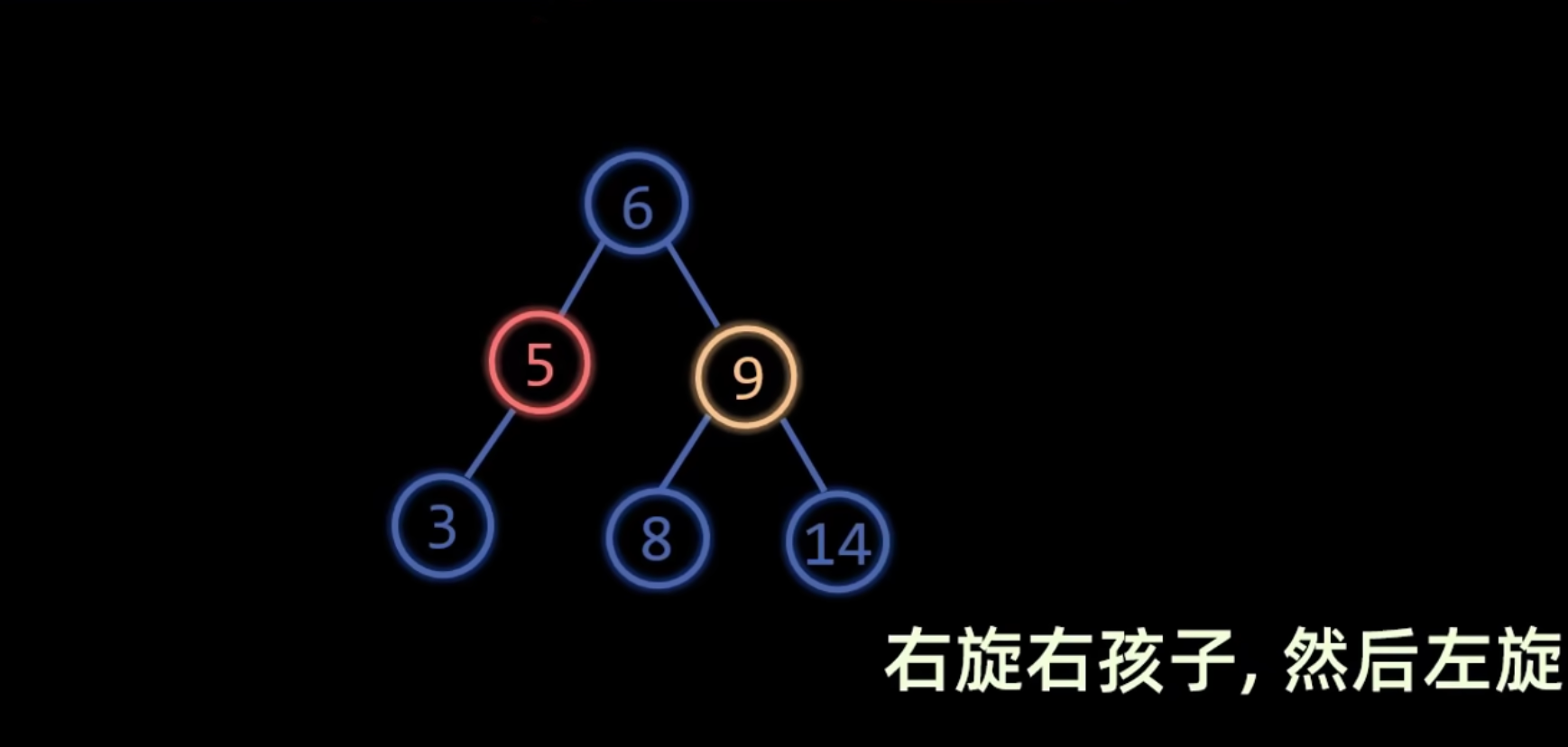
构造过程
构造一棵 AVL 树,就是从一棵空树开始,逐个插入元素。每插入一个元素,都必须执行上述的回溯与调整过程,检查是否需要进行旋转。
重要特性:在 AVL 树中,插入操作最多只需要进行一次旋转(单旋或双旋)就可以使整棵树恢复平衡。这是因为旋转操作会使调整后的子树高度恢复到插入前的高度,从而不会影响更高层祖先结点的平衡因子。
删除
AVL 树的删除操作比插入更复杂:
- 查找并删除:按照二叉排序树的规则删除结点。如果删除的是非叶子结点,可能需要用其中序前驱或后继来替代,问题最终转化为删除一个叶子结点或只有一个孩子的结点。
- 回溯与调整:从被删除结点的父结点开始(或者说,从实际被摘除的结点的父结点开始),向上回溯至根。
- 检查与旋转:检查路径上每个结点的平衡因子。如果发现失衡,则进行相应的旋转调整。
- 与插入不同:删除操作可能会导致回溯路径上的多个结点失衡。因此,删除操作可能需要进行多次旋转,直到回溯到根为止。一次旋转操作后,子树高度可能降低,从而影响其祖先结点,需要继续向上检查。
Case 1: 只有左/右子树
使用左/右子树代替它
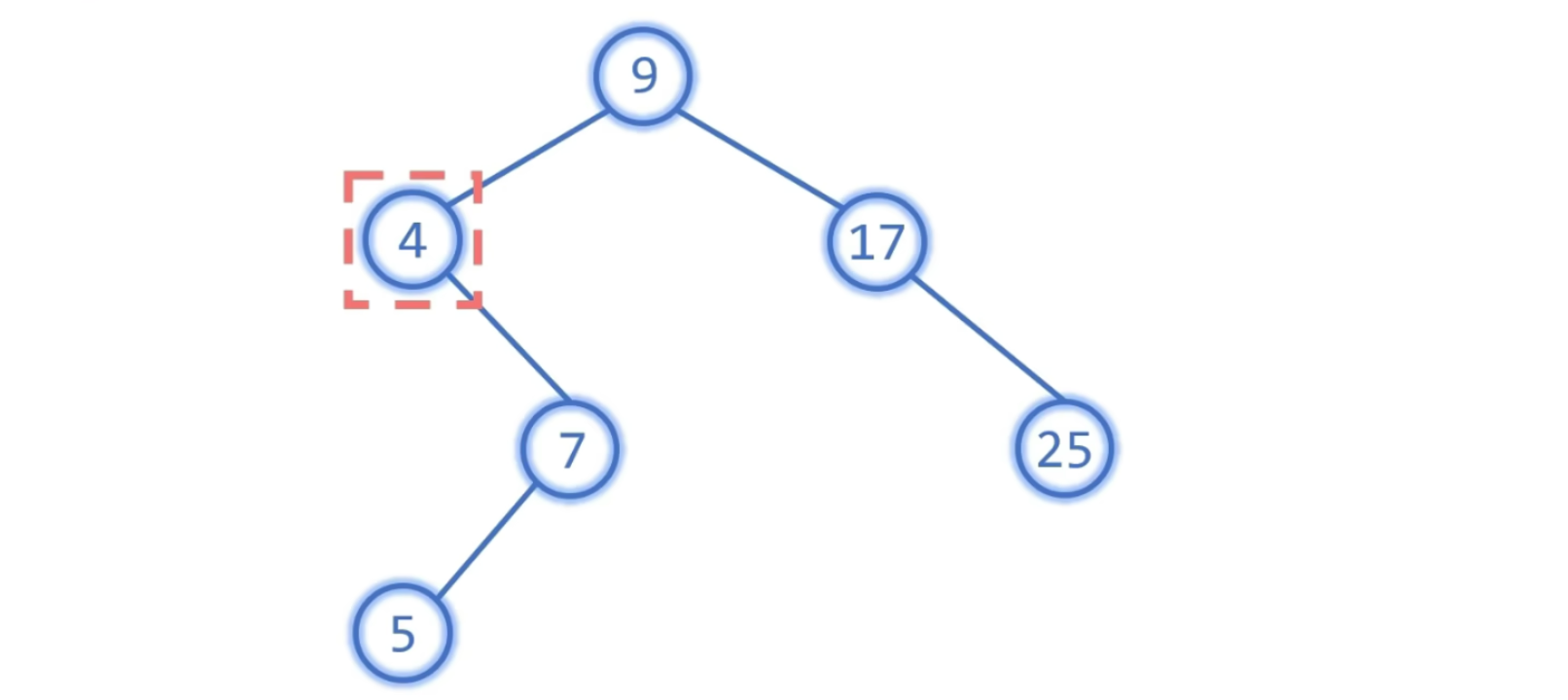
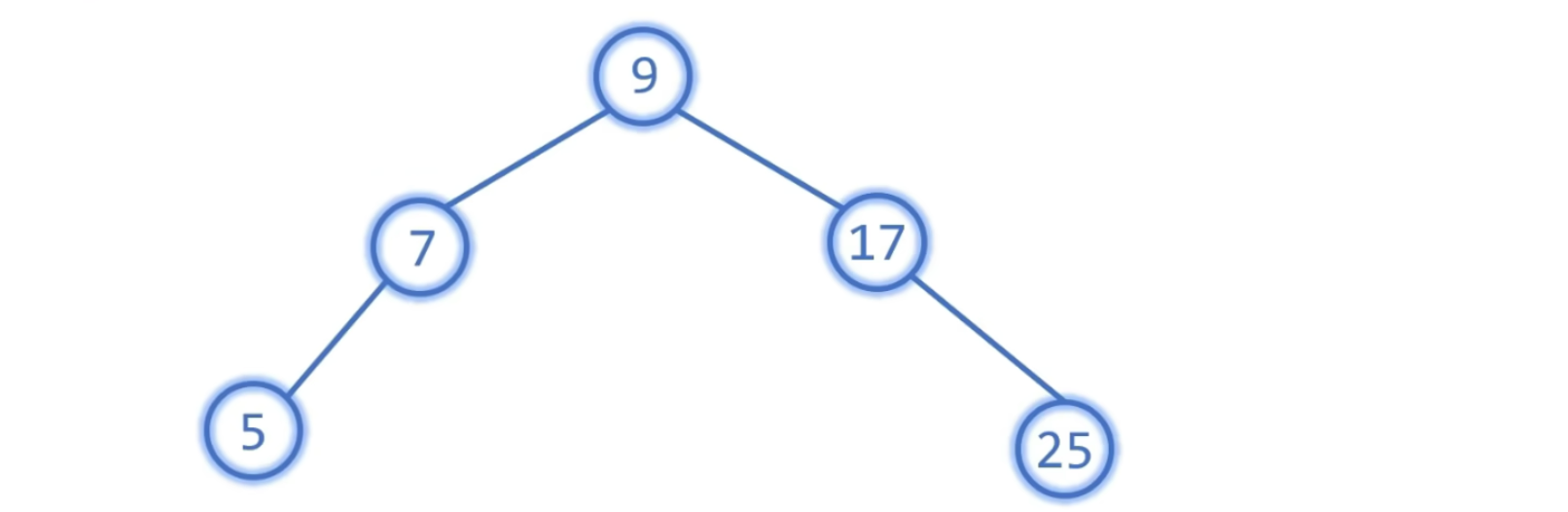
Case 2: 没有孩子
直接删除
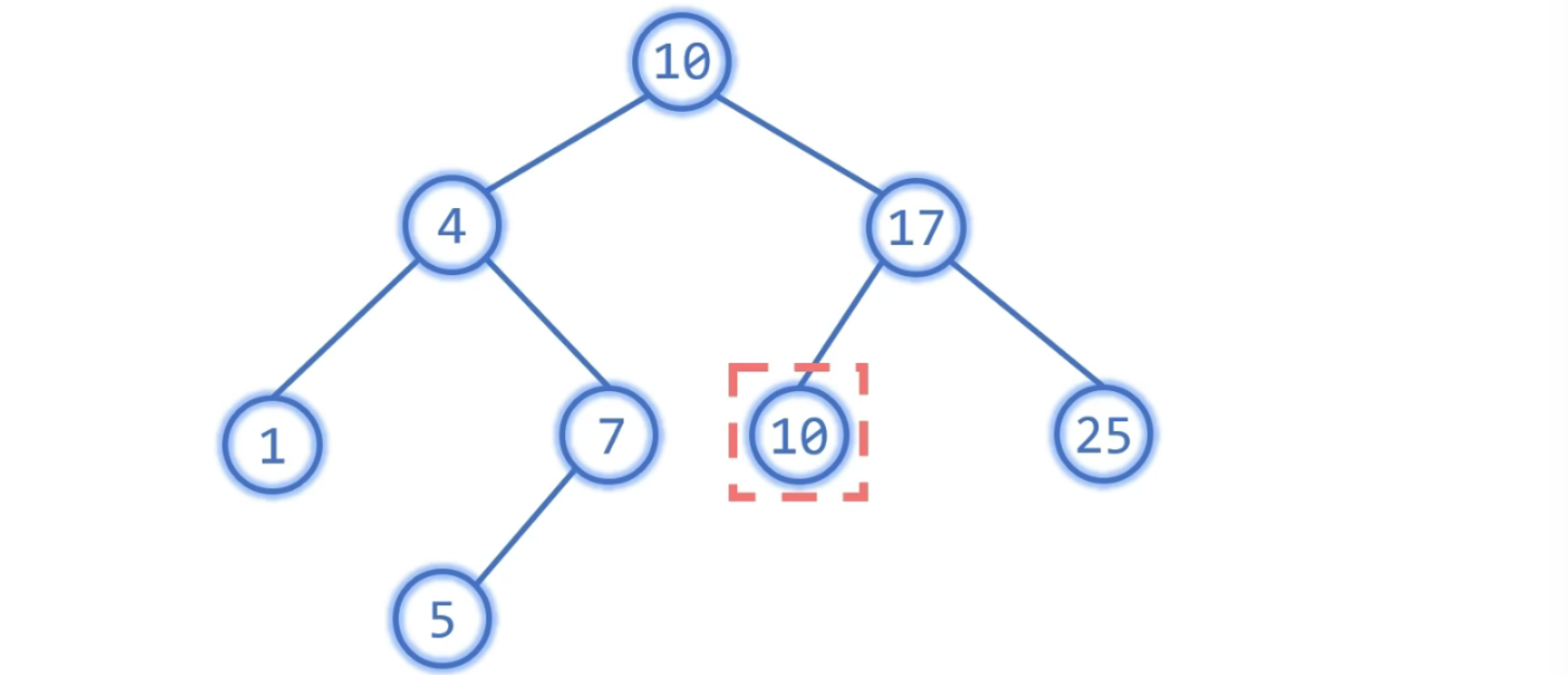
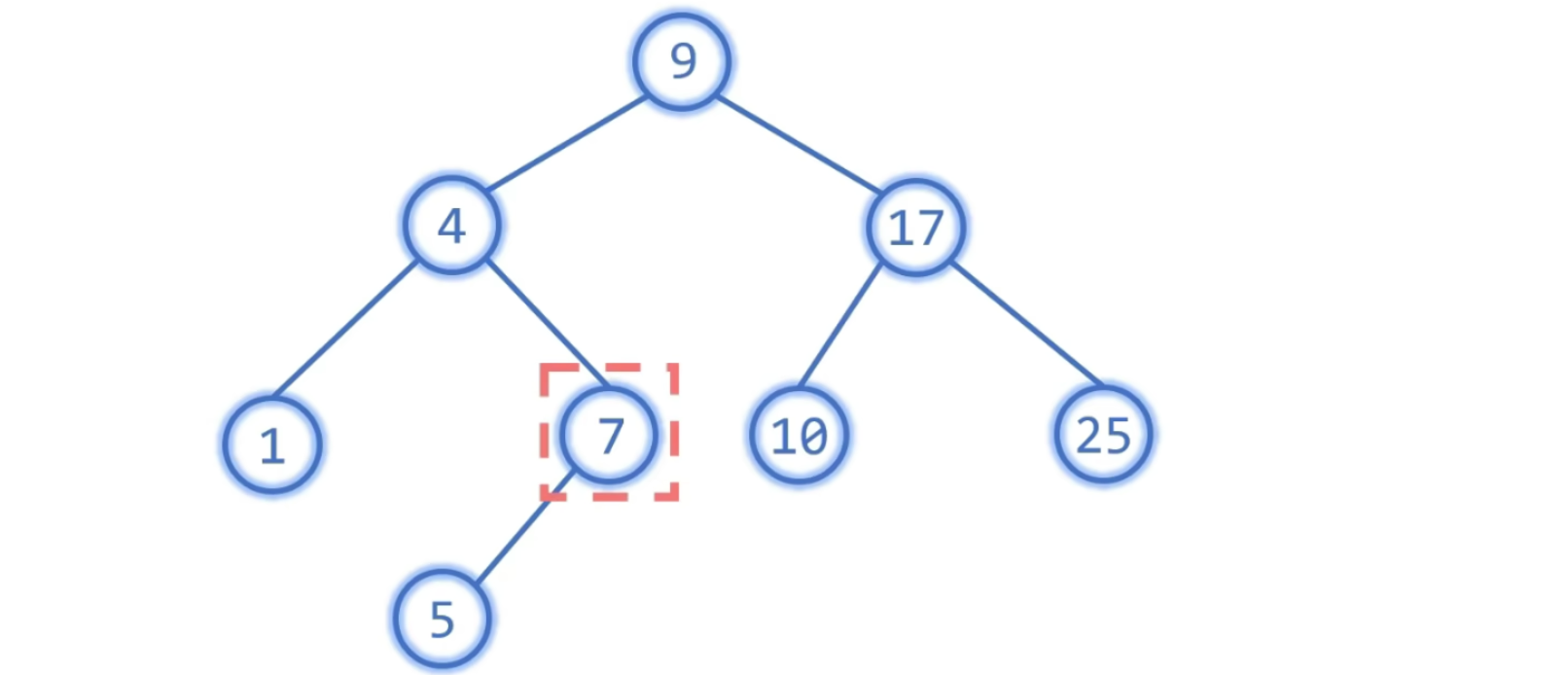
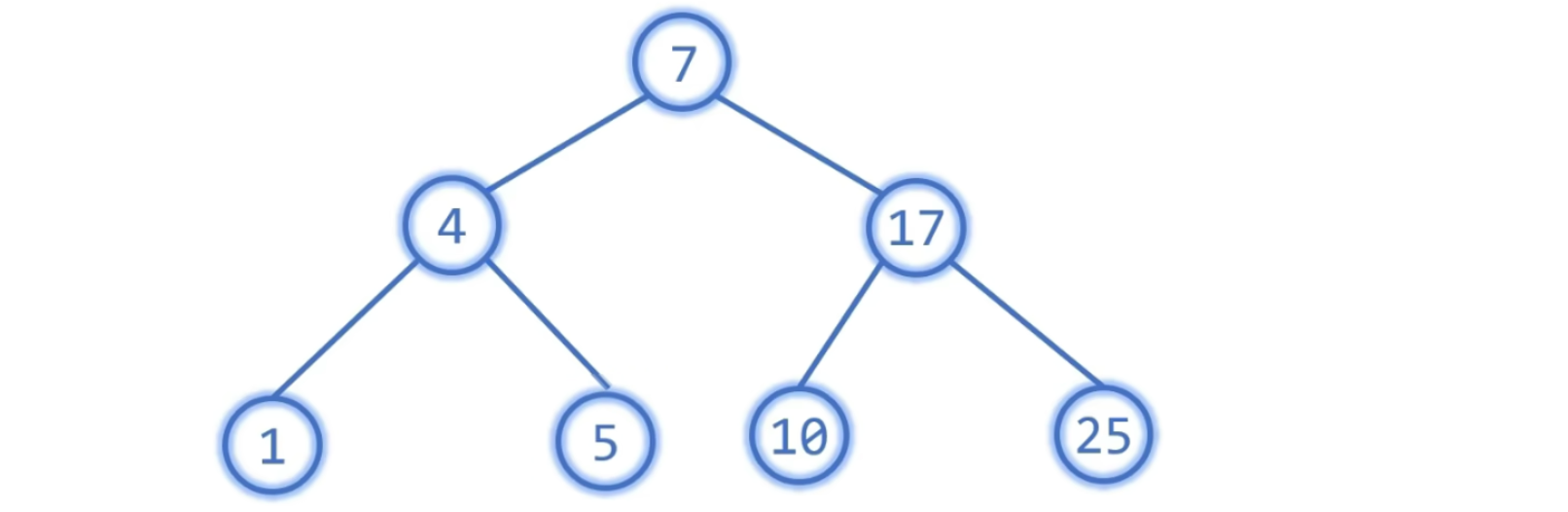
Case3: 左/右子树都有
直接后继 (或前驱) 代替之,然后删除原位置,即转为前两种情况
查找
AVL 树的查找操作与二叉排序树完全相同。
- 从根结点开始,比较关键字大小,决定向左子树或右子树查找,直至找到目标或遇到空指针。
- 效率:由于 AVL 树的高度被严格限制在 ,其查找操作的最坏时间复杂度也是 ,远优于普通二叉排序树的 。
其他性质
- 高度界限:一棵含有 个结点的 AVL 树,其高度 满足 ,即 的数量级是 。
- 最小结点数:高度为 的 AVL 树,其最少结点数 由以下公式给出: