702 顺序查找和折半查找

顺序查找和折半查找

效率指标

平均查找长度 (Average Search Length, ASL)

[[101 绪论#算法的复杂度#]]

顺序查找

一般顺序查找

从表的一端开始逐个比对，直到找到目标元素或遍历完整个表。

平均查找长度（ASL）

• 查找成功时：假设查找表中每个元素的概率相等，都为 $1/n$。

$$AS{L}_{成功}=\sum _{i=1}^n{P}_i{C}_i=\sum _{i=1}^n\frac{1}{n}\cdot i=\frac{1}{n}\sum _{i=1}^{n}i=\frac{n+1}{2}$$

• 查找失败时：需要与表中所有 $n$ 个元素都进行比较，且最后还需要一次与“空”的比较（即判断是否遍历完）。

$$AS{L}_{失败}=n+1$$

适用场景：适用于任何基于数组或链表存储的线性表，尤其适用于无序线性表。

有序表顺序查找

查找过程：从表的一端开始逐个比对。

• 如果当前元素等于目标元素，则查找成功。
• 如果当前元素大于目标元素（假设是升序排列），则查找失败且可提前终止（因为后续元素会更大，不再可能等于目标元素）。
• 如果遍历完整个表仍未找到，则查找失败。

平均查找长度（ASL）

• 查找成功时：与无序表顺序查找相同，每个元素被找到的概率及比较次数均未改变。

$$AS{L}_{成功}=\frac{n+1}{2}$$

• 查找失败时： 假设有 $n$ 个元素，有 $n+1$ 种失败情况（在第一个元素之前、在任意两个元素之间、在最后一个元素之后）。 假设每种失败情况的概率相等，都为 $1/(n+1)$。
  • 若目标值小于 $L_1$，比较 1 次。
  • 若目标值在 $L_i$ 和 $L_{i+1}$ 之间，比较 $i+1$ 次。
  • 若目标值大于 $L_n$，比较 $n$ 次。

$$AS{L}_{失败}=\frac{1}{n+1}\left(1+2+\cdots +n+n\right)=\frac{n}{2}+\frac{n}{n+1}$$

比较：

• 成功查找时：与无序表顺序查找的 $AS{L}_{成功}$ 相同，都为 $\frac{n+1}{2}$。
• 失败查找时：有序表顺序查找的 $AS{L}_{失败}=\frac{n(n+3)}{2(n+1)}$，而无序表为 $n+1$。当 $n$ 较大时，有序表的失败查找效率更高，因为可以提前终止比较。 例如，当 $n=9$ 时：
  • 无序表 $AS{L}_{失败}=9+1=10$
  • 有序表 $AS{L}_{失败}=\frac{9(9+3)}{2(9+1)}=\frac{9\times 12}{2\times 10}=\frac{108}{20}=5.4$ 显然，有序表的失败查找效率显著优于无序表。

折半查找

折半查找是一种高效的查找方法，仅适用于有序序列。它的基本思想是将查找范围逐步缩小一半，直到找到目标元素或查找范围为空。

• 初始时，将整个有序数组作为查找区间；
• 每次比较区间中间元素与目标值的大小：
  • 如果相等，则查找成功；
  • 如果目标值小，则查找左半区间；
  • 如果目标值大，则查找右半区间；
• 不断重复，直到区间为空或找到目标值。

时间复杂度：$O({\log }_{2}n)$

折半查找判定树（Decision Tree of Binary Search）

定义: 描述折半查找过程的二叉树。对于一个给定的有序序列，其折半查找判定树是唯一的。

性质

• 树的定义：树中的每个结点对应待查表中的一个记录，结点值为该记录的关键字。
• 树的性质：
  • 它是一棵二叉排序树 (BST)。
  • 对于任一结点，其左子树中所有结点的关键字均小于该结点的关键字，右子树中所有结点的关键字均大于该结点的关键字。
• 查找过程：折半查找的过程就是从根结点出发，按待查关键字与结点关键字的大小关系，选择走左分支或右分支，直到找到待查记录或走到叶子结点（查找失败） 为止。

判定树的构造

给定一个有序表 R[1..n]，其折半查找判定树的构造方法如下：

1. 根结点：根结点为 R[mid]，其中 mid = floor((1+n)/2)。
2. 左子树：根结点的左子树是 R[1..mid-1] 的折半查找判定树。
3. 右子树：根结点的右子树是 R[mid+1..n] 的折半查找判定树。
4. 递归构造：对子表递归执行上述步骤，直至所有子表为空。

形状特点

折半查找判定树是一棵平衡二叉树的特例，其平衡性体现在：

• 左子树元素的个数与右子树元素个数的差的绝对值最多为 1。
  • 这是因为每次都是从中间位置 mid 分割序列。
  • 取 mid = floor((low+high)/2) (向下取整) 时：左子树结点数 = mid - low，右子树结点数 = high - mid。当 high - low + 1 为奇数时，左右子树结点数相等；为偶数时，右子树比左子树多一个结点。即右子树结点数 ≥ 左子树结点数。
  • 取 mid = ceil((low+high)/2) (向上取整) 时：左子树结点数 = mid - low，右子树结点数 = high - mid。当 high - low + 1 为奇数时，左右子树结点数相等；为偶数时，左子树比右子树多一个结点。即左子树结点数 ≥ 右子树结点数。
• 树的高度：对于有 $n$ 个结点的折半查找判定树，其树高为 $h=\lfloor {\log }_{2}n\rfloor +1$ 或 $\lceil {\log }_2(n+1)\rceil$。这是所有形态的二叉排序树中高度最小的。
• 叶子结点：只有最下面一层或两层有叶子结点。
• 查找效率：查找成功时的比较次数最多不超过树的高度。平均查找长度 (ASL) 也与树高相关，数量级为 $O(\log n)$。

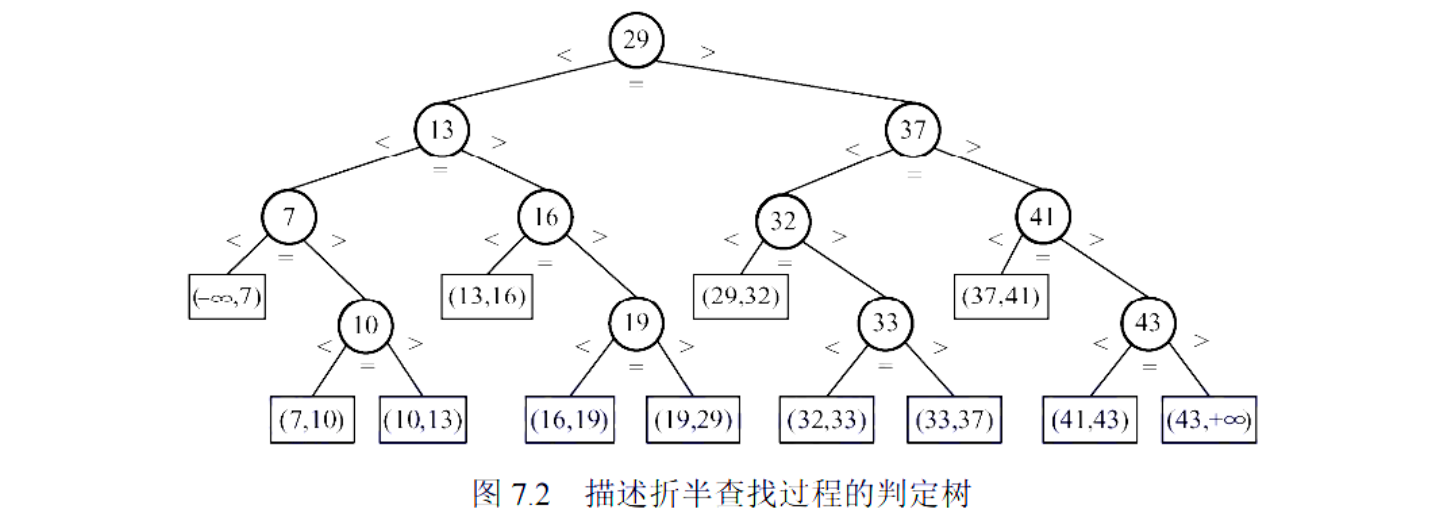
平均查找长度

• 成功查找长度：从根结点到查找成功结点（圆圈结点）的路径上的结点数。
• 失败查找长度：从根结点到查找失败结点（方框结点）的父结点的路径路径上的结点数。
• 平均查找成功长度 ($AS{L}_{succ}$): 所有内部节点的层数之和除以内部节点总数 $n$。

$$AS{L}_{succ}=\frac{1}{n}\sum _{i=1}^n\text{depth}(nod{e}_i)$$

• 平均查找失败长度 ($AS{L}_{unsucc}$): 所有外部节点的层数之和除以外部节点总数 $n+1$。

$$AS{L}_{unsucc}=\frac{1}{n+1}\sum _{i=0}^n\text{depth}(failure\_nod{e}_i)$$

最多比较次数

定义: 查找一个元素所需的最大比较次数，即折半查找判定树的高度 $H$。

• 计算公式: 对于包含 $n$ 个元素的有序表，其判定树的高度为 $H=\lfloor {\log }_{2}n\rfloor +1$。
• 时间复杂度: 折半查找的最坏时间复杂度为 $O({\log }_{2}n)$。
• 示例 (根据图 7.2): $n=11$, $H=\lfloor {\log }_{2}11\rfloor +1=3+1=4$。这与图中树的高度相符。

适用场景

1. 前提条件: 查找表必须是有序的，并且采用顺序存储结构（如数组），以便支持随机访问。
2. 优点: 查找效率高，时间复杂度为 $O({\log }_{2}n)$。
3. 缺点: 插入和删除操作困难。由于维持表的有序性，插入或删除一个元素平均需要移动 $O(n)$ 个元素。
4. 结论: 折半查找特别适用于静态查找表或不经常进行插入和删除操作的有序表。对于需要频繁增删的动态表，应考虑使用二叉排序树、AVL 树或 B 树等数据结构。

分块查找

也称索引顺序查找，是顺序查找和折半查找的一种折中方案。它吸取了两种查找的优点，既有类似于动态链表的结构特点，又适于快速查找。

基本思想：将 n 个数据元素 “分块有序”，即把表分成若干块，块与块之间是有序的，即第 i 块中的所有元素都小于第 i+1 块中的所有元素。但每个块内部的元素不要求有序。

结构

1. 索引表：存放每个数据块的最大关键字和该块在主存中的起始地址。索引表是按关键字有序排列的。
2. 数据块：存储数据记录，块内记录可无序。

查找过程

• 在索引表中确定待查记录所在的块：由于索引表是按关键字有序的，因此既可以采用 顺序查找，也可以采用 折半查找 来确定待查记录所在的块。
• 在块内顺序查找对应记录：根据索引表中给出的起始地址，在对应的块内进行 顺序查找。

平均查找长度

分块查找的平均查找长度 (ASL) 是查找索引表和在块内查找的长度之和，即 $ASL=L_I+L_B$。

假设共有 $n$ 个记录，均匀地分为 $b$ 块，每块有 $s$ 个记录，则 $n=b\times s$。

1. 查找索引表 ($L_I$):

   • 若对索引表进行 顺序查找，则平均查找长度为 $L_I=(b+1)/2$。
   • 若对索引表进行 折半查找，则平均查找长度为 $L_I\approx {\log }_2(b+1)$。

2. 块内查找 ($L_B$):

   • 在块内进行 顺序查找，平均查找长度为 $L_B=(s+1)/2$。

ASL 分析与优化 (以索引表顺序查找为例):

• 总平均查找长度为：$ASL=L_I+L_B=\frac{b+1}{2}+\frac{s+1}{2}$。
• 将 $s=n/b$ 代入，得 $ASL=\frac{1}{2}(b+\frac{n}{b}+2)$。
• 为使 ASL 最小，需要使 $b+n/b$ 的值最小。根据均值不等式，当 $b=n/b$ 时，即 $b=\sqrt{n}$ 时，该值最小。
• 因此，当块数 $b$ 和块内元素数 $s$ 都约等于 $\sqrt{n}$ 时，平均查找长度取最小值。
• 最小 ASL：$AS{L}_{min}=\frac{\sqrt{n}+1}{2}+\frac{\sqrt{n}+1}{2}=\sqrt{n}+1$。

性能比较

查找方法	平均查找长度 (ASL)	时间复杂度	前提条件
顺序查找	$(n+1)/2$	$O(n)$	无
折半查找	$\approx {\log }_2(n+1)$	$O(\log n)$	顺序存储，有序
分块查找	$\approx \sqrt{n}+1$ (最优)	$O(\sqrt{n})$	分块有序