21 导数与微分

导数概念

定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域内有定义，当自变量 $x$ 在 $x_0$ 处取得增量 $\Delta x$ (点 $x_0+\Delta x$ 仍在该邻域内) 时，相应地函数取得增量 $\Delta y=f(x_0+\Delta x)-f(x_0)$。如果极限

$$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

存在，则称函数 $y=f(x)$ 在点 $x_0$ 处可导，并称该极限为函数在点 $x_0$ 处的导数，记作 $f^{\prime }(x_0)$ 或 ${\frac{dy}{dx}|}_{x=x_0}$。

常用定义的等价形式

• $f^{\prime }(x_0)=\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}$
• $f^{\prime }(x_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$

左导数与右导数

右导数: $f_{+}^{\prime }(x_0)=\underset{\Delta x\to 0^{+}}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ 左导数: $f_{-}^{\prime }(x_0)=\underset{\Delta x\to 0^{-}}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ 可导的充要条件：函数 $f(x)$ 在点 $x_0$ 处可导 $⟺$ 其左、右导数均存在且相等，即 $f_{+}^{\prime }(x_0)=f_{-}^{\prime }(x_0)$。

微分概念

定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域内有定义，如果函数的增量 $\Delta y=f(x_0+\Delta x)-f(x_0)$ 可表示为

$$\Delta y=A\cdot \Delta x+o(\Delta x)$$

其中 $A$ 是不依赖于 $\Delta x$ 的常数，则称函数 $y=f(x)$ 在点 $x_0$ 可微，称 $A\cdot \Delta x$ 为函数在点 $x_0$ 的微分，记作 $dy$，即 $dy=A\cdot \Delta x$。通常记自变量的增量 $\Delta x$ 为 $dx$，则 $dy=A\cdot dx$。

可微充要条件

函数 $f(x)$ 在点 $x_0$ 可微 $⟺$ 函数 $f(x)$ 在点 $x_0$ 可导。

其中，$A=f^{\prime }(x_0)$，因此 $dy=f^{\prime }(x)dx$。

导数与微分的几何意义

导数——曲线斜率

导数 $f^{\prime }(x_0)$ 在几何上表示曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处切线的斜率，即 $k=\tan \alpha =f^{\prime }(x_0)$ (其中 $\alpha$ 为切线倾斜角)。

• 切线方程: $y-f(x_0)=f^{\prime }(x_0)(x-x_0)$
• 法线方程: $y-f(x_0)=-\frac{1}{f^{\prime }(x_0)}(x-x_0)$ (要求 $f^{\prime }(x_0)\ne 0$)

微分——切线增量

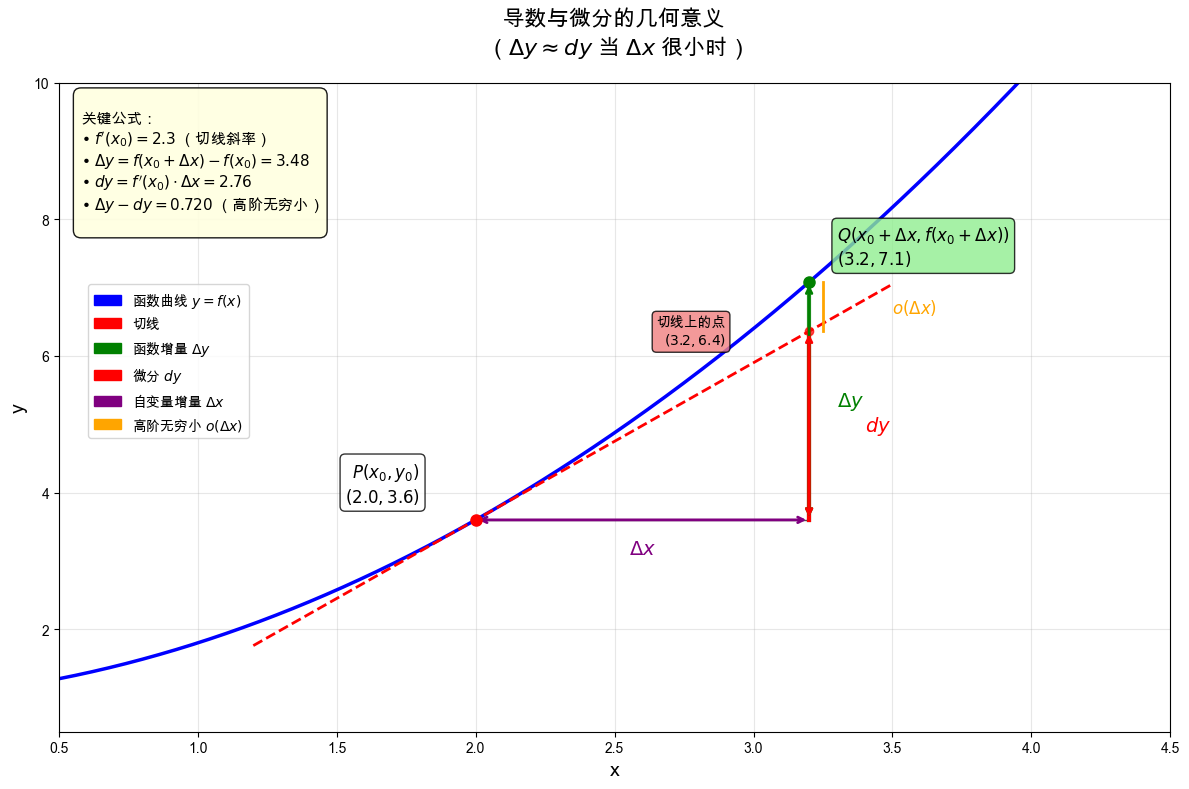
微分 $dy=f^{\prime }(x_0)dx$ 表示当自变量从 $x_0$ 变化到 $x_0+dx$ 时，曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处切线纵坐标的增量。

当 $|\Delta x|$ 很小时，$\Delta y\approx dy$，即函数增量约等于微分。

连续、可导、可微之间的关系

• 可导（可微）$\Rightarrow$ 连续：若函数在某点可导，则它在该点必定连续。
• 连续 $\nRightarrow$ 可导（可微）：函数在某点连续，但未必可导。例如，$y=|x|$ 在 $x=0$ 处连续但不可导。
• 可导 $⟺$ 可微：对于一元函数，可导与可微是等价的。

求导公式

• $(C{)}^{\prime }=0$ ($C$ 为常数)
• $(x^{\alpha }{)}^{\prime }=\alpha x^{\alpha -1}$
• $(a^x{)}^{\prime }=a^x\ln a$
• $(e^x{)}^{\prime }=e^x$
• $({\log }_{a}x{)}^{\prime }=\frac{1}{x\ln a}$
• $(\ln x{)}^{\prime }=\frac{1}{x}$
• $(\sin x{)}^{\prime }=\cos x$
• $(\cos x{)}^{\prime }=-\sin x$
• $(\tan x{)}^{\prime }={\sec }^{2}x$
• $(\cot x{)}^{\prime }=-{\csc }^{2}x$
• $(\sec x{)}^{\prime }=\sec x\tan x$
• $(\csc x{)}^{\prime }=-\csc x\cot x$
• $(\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}$
• $(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$
• $(\arctan x{)}^{\prime }=\frac{1}{1+x^2}$
• $(\text{arccot }x{)}^{\prime }=-\frac{1}{1+x^2}$

求导法则

四则运算法则

• $(u\pm v{)}^{\prime }=u^{\prime }\pm v^{\prime }$
• $(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$
• $(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$ ($v\ne 0$)

复合函数求导法

若 $y=f(u)$， $u=g(x)$ 均可导，则复合函数 $y=f[g(x)]$ 可导，且

$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}=f^{\prime }(u)\cdot g^{\prime }(x)$$

核心：由外向内，逐层求导。

隐函数求导法

由方程 $F(x,y)=0$ 确定的隐函数 $y=y(x)$，求导方法：

1. 方程两边同时对 $x$ 求导，视 $y$ 为 $x$ 的函数，利用复合函数求导法。
2. 解出 $\frac{dy}{dx}$。
3. 公式法：若 $F(x,y)$ 偏导数连续，则 $\frac{dy}{dx}=-\frac{F_x^{\prime }(x,y)}{F_y^{\prime }(x,y)}$ (其中 $F_y^{\prime }(x,y)\ne 0$ )。

反函数的导数

设 $y=f(x)$ 可导且 $f^{\prime }(x)\ne 0$，其反函数为 $x=g(y)$，则反函数也一定可导，且

$$g^{\prime }(y)=\frac{1}{f^{\prime }(x)}\text{或}\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}$$

参数方程求导法

设 $y=y(x)$ 是由参数方程 $\{\begin{array}{l}x=\phi (t)\\ y=\psi (t)\end{array}$ 所确定，且 $\phi (t),\psi (t)$ 可导，${\phi }^{\prime }(t)\ne 0$，则

$$\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{{\psi }^{\prime }(t)}{{\phi }^{\prime }(t)}$$

二阶导数：

$$\frac{d^{2}y}{d{x}^2}=\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d(\frac{{\psi }^{\prime }(t)}{{\phi }^{\prime }(t)})/dt}{dx/dt}=\frac{{\psi }^{\prime \prime }(t){\phi }^{\prime }(t)-{\psi }^{\prime }(t){\phi }^{\prime \prime }(t)}{[{\phi }^{\prime }(t){]}^3}$$

对数求导法

适用场景：

1. 幂指函数 $y=[u(x){]}^{v(x)}$。
2. 多个函数连乘、连除、开方。

方法：两边取自然对数 $\ln y=\ln f(x)$，然后对方程两边同时对 $x$ 求导，最后解出 $y^{\prime }$。

高阶导数

若函数 $f(x)$ 的导数 $f^{\prime }(x)$ 依然可导，则称 $f^{\prime }(x)$ 的导数为 $f(x)$ 的二阶导数，记作 $y^{\prime \prime }$ 或 $f^{\prime \prime }(x)$ 或 $\frac{d^{2}y}{d{x}^2}$。

一般地，$n-1$ 阶导数的导数称为 $n$ 阶导数，记作 $y^{(n)}$ 或 $f^{(n)}(x)$ 或 $\frac{d^{n}y}{d{x}^n}$。

常用高阶导数公式

• $(e^{ax}{)}^{(n)}=a^n{e}^{ax}$
• $(a^x{)}^{(n)}=(\ln a{)}^n{a}^x$
• $(\sin (ax+b){)}^{(n)}=a^n\sin (ax+b+\frac{n\pi }{2})$
• $(\cos (ax+b){)}^{(n)}=a^n\cos (ax+b+\frac{n\pi }{2})$
• $(x^{\mu }{)}^{(n)}=\mu (\mu -1)\cdots (\mu -n+1)x^{\mu -n}$
• $(\ln (ax+b){)}^{(n)}=(-1{)}^{n-1}\frac{(n-1)!a^n}{(ax+b{)}^n}$
• $(u\pm v{)}^{(n)}=u^{(n)}\pm v^{(n)}$
• 莱布尼茨 (Leibniz) 公式： $(uv{)}^{(n)}={\sum }_{k=0}^n{C}_n^k{u}^{(k)}{v}^{(n-k)}$，其中 $C_n^k=\frac{n!}{k!(n-k)!}$，$u^{(0)}=u,v^{(0)}=v$。